ESTA PÁGINA ESTÁ PENSADA PARA LA ESO, SI NECESITAS FUNCIONES Y GRÁFICAS DE BACHILLERATO VISITA: MATEMÁTICAS EN EL BACHILLERATO Ó CUADERNO 2º BACH
4ª Parte: Funciones y sus gráficas
Relaciones funcionales.
Estudio gráfico y algebraico de funciones[1].
Interpretación de gráficas
1. Un médico dispone de 1hora diaria para consulta. El tiempo que podría, por término medio, dedicar a cada enfermo, depende del número de ellos que se acudan:
1 enfermo 60
minutos
2 enfermos 30
minutos
3 enfermos 20
minutos
..... ....... ......... ......
Así hasta un máximo de 30 enfermos. Si llamamos x al número de enfermos e y al de minutos dedicados a cada enfermo escribe la expresión funcional que existe entre ellas ¿ Cómo es la variable independiente, continua o discreta? Dibuja la gráfica ¿ Tiene sentido unir los puntos de la gráfica con una línea?
2. En unos aparcamientos públicos figura la siguiente tarifa de precios:
Tarifa
1ª
hora o fracción 1 €
Cada
hora más o fracción 0,8 €
Máximo 12 € por 24 horas
Haz una gráfica representativa de la función : tiempo de aparcamiento ....... coste
3. Si un coche va a 80km por hora, ¿ que espacio habrá recorrido al cabo de 2, 3, y 3,5 horas?
a) Dibuja la gráfica de la función espacio-tiempo.
b) ¿Qué tiempo empleará en recorrer 200 y 320km?
Solución
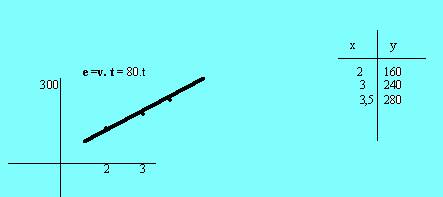
b) Despejando el tiempo tendremos t =e/v:
t = 200/80 = 5/2 = 2horas y media y t = 320/80 =4 horas
4. Representa los siguientes pares (x, y) . Indica la relación entre las variables x e y:
|
x |
1 |
3 |
4 |
5,5 |
7 |
.... |
|
y |
0,75 |
2,25 |
3 |
4,125 |
5,525 |
.... |
5. Dada la tabla
|
x |
0 |
1 |
2 |
3 |
4 |
.... |
|
y |
1 |
3 |
5 |
7 |
9 |
.... |
Representa estos puntos en un sistema de ejes coordenados y escribe la ecuación de la función que relaciona las variables x e y.
6. Halla el dominio de las siguientes funciones:
a) y = 3x b) y = x2-3
c) y = 
D =R + d)
y = 1/x D = R -{0}
e) 
f)
7. Estudia la continuidad de las siguientes funciones:
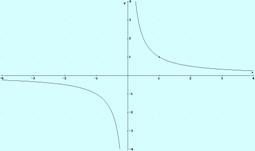
a)
Continua excepto en el x =0.
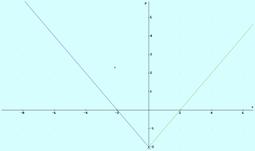
b)
Continua en todos los puntos.
8. Estudia la continuidad de las siguientes funciones:
a)
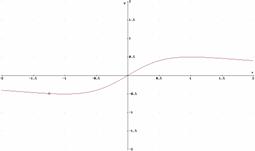
b)
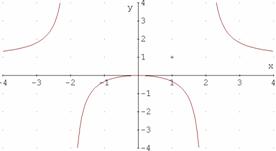
9. Para las funciones del ejercicio
anterior. Estudia la monotonía, simetría y los máximos y mínimos.
b) creciente en ]-4, -2[ È]-2, 0[ y decreciente en ]0, 2[È]2, 4 [
simétrica respecto el eje OY
no tiene mínimo, el máximo relativo se alcanza en el 0 y vale 0
10. Estudia la monotonía, simetría y los máximos y mínimos de la función cuya gráfica es la de la figura.
 |
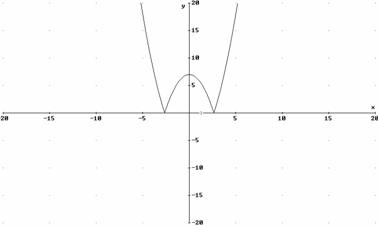11. Antonio ha comprado un coche que le ha costado 19500 €. El coche se deprecia un 20% cada año. Al cabo de un tiempo decide venderlo y le dan 5200 € . ¿Cuántos años han pasado?
Indicación: Haz la gráfica de la situación planteada y encuentra el punto de la gráfica cuya ordenada valga 5200.
12. Dibuja en el intervalo [0, 6] la función que a cada número positivo le hace corresponder su parte entera.
13. Halla la pendiente de las rectas que pasan por los puntos:
a) (2. 3) y (-1, 0)
b) (3, 1) y (4, -5) . Solución
14. Halla la pendiente de las rectas:
a) y = -3x +1
b) y = 2-x
c) 3x-2y-4=0
d) 
15. Representa las siguientes funciones lineales o afines:
a) y =2x ;
b) y =3; c) y = 3x-2; d)
; e) 
16. Halla gráficamente la pendiente de la recta que pasa por los puntos A(-3, -6) y B((3, -2) y escribe su ecuación.
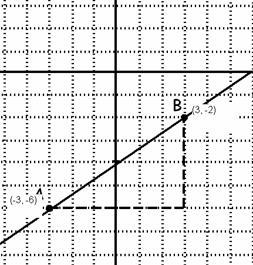Solución
La pendiente según se ve en la gráfica es
la ordenada en el origen es -4
y por tanto la ecuación es
17. Dibuja y halla la ecuación de la recta que pasa por los puntos:
a) (2. 3) y (-1, 0)
b) (3, 1) y (4, -5)
18. Hallar la ecuación de cada una de las siguientes rectas:
a) Pasa por el punto (0, 1) y tiene por pendiente 3
b) Pasa por el punto (0, 4) y tiene por pendiente 3/4
c) Pasa por el punto (-3, 3) y tiene por pendiente -4
19. Calcula la expresión de la función cuya gráfica se adjunta:
Solución
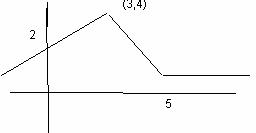Es
una función definida a trozos.
El primer trozo pertenece a la recta que pasa por los
Puntos (0,2) y (3,4), Su ecuación es
y = 2x +2
El otro trozo pertenece a la recta que pasa por (3, 4) y (5, 1).
La
pendiente es: 
y
= 
El último trozo pertenece a la recta constante y =1
La
función es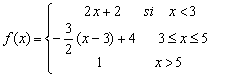 
20. Calcula la expresión algebraica de la función cuya gráfica es:
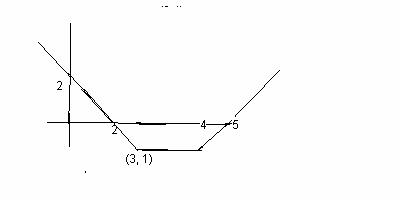
21. Representa en los mismos ejes coordenados las siguientes rectas:
a) y = x e y = 2 – x
Solución
 |
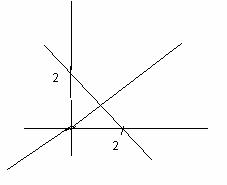Las rectas se cortan en el punto (1, 1)
b) y = x-3 e y = -x +2;
c) 
e 
22. Representa la gráfica de la función cuadrática y =x2 -3x+2
Solución
Es una parábola. Necesitamos calcular el vértice y los puntos de corte con los ejes
Vértice. La abscisa del vértice está
en el punto 
, en nuestro caso:
; 
Los puntos de corte con los ejes:
punto (0,2) 
x =1, x =2 puntos (1, 0) y (2, 0)
Con estos puntos podemos dibujar la gráfica pues tenemos entre ellos dos puntos simétricos:
 |
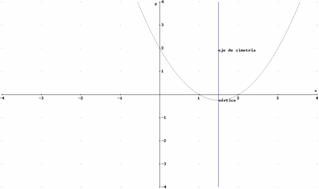23. Representa las siguientes parábolas indicando el vértice y los puntos de corte con los ejes.
a) y =x2
; b)
; c) y = -3x2 +6; d) y = x2
+x +1; e) y = x2 -5x+6; f) y =-x2 +3x-2
24. Dibuja en unos mismos ejes cartesianos la recta y = x- 3 y la parábola y = x2 -5x+6.
25. Resuelve gráficamente los siguientes sistemas:
a)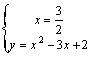 
Se dibujan sobre los mismos ejes
(ver ejercicio 22)
Solución V (3/2, -1/4)
b) 
c)
26. Un viajero llega tarde a la estación y el tren ya ha salido.
Si las ecuaciones de las trayectorias del viajero y del tren son:
Tren: 
Viajero 
indica si el viajero alcanza el tren y en este último caso el momento del encuentro.
27.
Resuelve analítica y gráficamente el
sistema: 
28. El coste de producción de x unidades diarias de un determinado artículo es:
y el precio de venta de uno de ellos es (50-x/4) €
Halla el número de unidades que debe venderse diariamente para que el beneficio sea máximo.
Solución
La expresión de la función beneficio es:
B(x)=(50-x/4)x –((1/4)x2 +
35x + 25) = 
, función cuadrática.
La solución gráfica se ve en la figura, es el vértice de la parábola.
 |
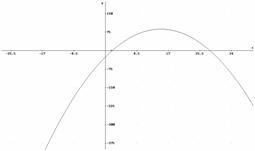x = 15 unidades.
29. Representa las siguientes funciones usando una tabla de valores adecuada:
a) 
; b) 
; c) 
: d) 
; e) 
Solución
b).figura 1
|
x |
-1 |
0 |
1 |
3 |
... |
|
|
y |
1 |
2 |
2,4142 |
3 |
... |
|
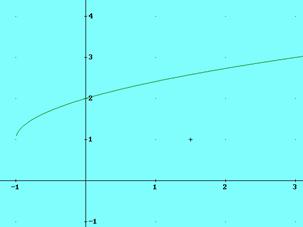
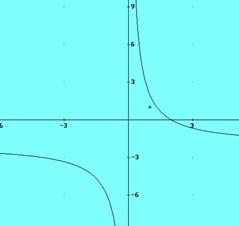
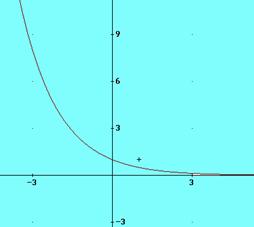
figura 1 figura 2 figura 3.
30. Representa las siguientes funciones de proporcionalidad inversa:
a) 
; b) 
; c) 
; d) 
(figura 2)
31. Representa las siguientes funciones exponenciales:
a) y = 3x ; b) y = 2- x ; c) y = (1/2)-x figura 3
32. Un capital de 12000 € está colocado al 3% fijo anual. Calcula la expresión que nos da el capital acumulado al cabo de t años.
Solución
Se trata de una función de crecimiento exponencial.
El capital en el primer año se convertirá 12000+12000.0,03= 12000(1+0,03)=12000.1,03= C1,
El capital al cabo de 2 años se convertirá C1 + C1.0,03 = C1(1,03) =12000. (0,03)2 ...
y
al cabo de t años C(t)=12000.(1,03)t t
0
33. Una sustancia radiactiva tiene un periodo de semi-desintegración de 15 años. Tenemos 10 gramos de esa sustancia. Encontrar la función que nos da la cantidad de sustancia radiactiva en función del tiempo transcurrido
34. Un virus se reproduce por división transversal: en 2 horas cada virus se divide en tres. En el día 0 se ha contado un millón de virus de ese tipo y se estudia la evolución de esta población en función del tiempo.
a) Encontrar la expresión de la población en función del tiempo, en horas.
b) ¿Cuál es el efectivo de la población en la primera hora?
c) ¿Cuánto tiempo tardará en doblarse? ¿Y en multiplicarse por 10?
Cuaderno de actividades de 4º ESO Anexo
