Cuaderno de actividades 4º ESO
ESTE PÁGINA SE PUEDE DESCARGAR COMO ARCHIVO ZIP, Y EXISTE EN FORMATO pdf
INTRODUCCIÓN:
La Estadística descriptiva es una parte de la Estadística cuyo objetivo es examinar a todos los individuos de un conjunto para luego describir e interpretar numéricamente la información obtenida.
Sus métodos están basados en la observación y el recuento. Se pretende, una vez realizados, poder simplificar los datos observados para obtener de ellos una información lo más completa posible del total de la población.
En estadística descriptiva el material de trabajo lo constituyen los datos, que son los resultados de las observaciones. Una vez obtenidos los datos hay que ordenarlos y clasificarlos mediante algún criterio racional de modo que sea posible una visión crítica de los mismos.
En general, este tratamiento previo de los datos será de alguno de estos tres tipos:
1) Construcción de tablas para ordenar y clasificar los datos.
2) Realización de gráficos para representar físicamente los datos.
3) Obtención de estadísticos o funciones de los valores de los datos, que pretenden poner de manifiesto ciertas propiedades de los mismos.
Estadística Unidimensional [1]
Conceptos básicos.
Cualquier elemento o ente que sea portador de información sobre alguna propiedad en la cual se está interesado se denomina individuo.
El conjunto de todos los individuos en los que se desea estudiar alguna propiedad o característica se llama población.
Todo subconjunto finito de la población sobre el que se realice el estudio de la propiedad deseada, es una muestra. Al número de individuos de este subconjunto se le llama tamaño de la muestra.
Ejemplo 1. Para estudiar la evolución del cáncer de mama en la población femenina de un país, se puede considerar que individuo es cada una de las mujeres residentes en el mismo, población es el conjunto de todas ellas y una muestra se obtiene al observar el 1% del censo.
Con mucha frecuencia se consideran como población y muestra, no los conjuntos de individuos, sino las medidas de la característica asociadas a esos individuos.
Ejemplo 2. En un banco de sangre se experimenta un nuevo sistema para aumentar el período de conservación de la misma. En este caso cada bolsa de sangre es un individuo; la población es el conjunto de todas las bolsas del banco y una muestra se obtiene tomando un cierto número de bolsas para su análisis.
Obsérvese que el concepto de individuo no va asociado necesariamente con el de persona, sino que puede ser algo de naturaleza más abstracta.
Clasificación de los datos.
Cuando los datos, es decir los resultados de las observaciones, no son magnitudes medibles numéricamente, sino cualidades o atributos, se dice que se trata de datos cualitativos, mientras que en caso contrario se habla de datos cuantitativos.
Ejemplo 3. Se observan las causas de muerte de 16 individuos de una cierta población, agrupándolas en las cuatro siguientes: enfermedades cardiovasculares (EC), cáncer (C), accidentes (A) y otras causas (O), habiéndose obtenido los siguientes datos:
EC, EC, A, C, O, A, EC, A, O, C,EC, C, O, C y EC.
Como los resultados no son medibles numéricamente, los datos son cualitativos.
Ejemplo 4. Las notas obtenidas en Matemáticas en una clase de COU han sido:
2, 7, 4, 6, 5, 0, 3, 9, 8, 4, 3, 6, 5 y 8.5. Se trata de datos cuantitativos.
A su vez los datos cuantitativos se denominan continuos si los resultados pueden tomar cualquier valor real dentro de un cierto intervalo, o discretos, si sólo pueden tomar ciertos valores particulares.
Ejemplo 5. Del estudio de la estatura de un cierto núcleo de población se han obtenido los siguientes datos: 1.62, 1.78, 1.75, 1.58, 1.83, 1.68 y 1.81metros.
Son datos continuos, pues los individuos de una población pueden tener como estatura cualquier número real en un cierto intervalo.
Ejemplo 6. Del alumbramiento de un conjunto de ratas se ha observado el número de crías, obteniéndose los siguientes valores numéricos: 5, 3, 1, 5, 3, 6, 4, 2, 5, 6, 3, 6, 5, 2, 6, 7 y 3.
Por no ser posibles números no naturales, es evidente que se trata de datos cuantitativos discretos.
 Es decir los datos se
clasifican:
Es decir los datos se
clasifican:
Los datos pueden provenir del estudio de un sólo carácter o propiedad (caso unidimensional) o de varios simultáneamente (caso multidimensional).
3. Variables estadísticas. Frecuencias.
Los caracteres estadísticos de una población son las propiedades o cualidades de los individuos que nos interesa estudiar. Un carácter estadístico divide a la población en clases. A cada una de estas clases se la denomina modalidad.
Cuando el carácter es cuantitativo sus diversas modalidades son medibles, es decir se les puede asignar un número.
Definición 1. Se llama variable estadística a la aplicación que a cada modalidad le hace corresponder ese número, es decir su medida.
Ejemplo 7. En el ejemplo 6 la variable estadística toma los valores: 1, 2, 3, 4, 5, 6 y 7.
La variable estadística será discreta cuando sólo pueda tomar un nº finito de valores y continua cuando pueda tomar todos los valores de un cierto intervalo.
Ejemplo 8. La variable estadística del ejemplo 5 es continua y discreta la del ejemplo 6.
Definición 2. Se llama frecuencia absoluta al número de individuos que toman un determinado valor de una variable estadística (o una modalidad de un atributo).
Para variables estadísticas (es decir, datos cuantitativos) puede definir:
Definición 3. Se llama frecuencia absoluta acumulada de un valor a la suma de las frecuencias absolutas de todos los valores menores o iguales que él.
Ejemplo 9. En el ejemplo 6 la frecuencia absoluta del 5 (tener 5 crías) es 4. La frecuencia absoluta acumulada del 2 es 3.
Definición 4. Se llama frecuencia relativa a la razón entre la frecuencia absoluta y el número total de datos o tamaño de la población.
Definición 5. Se llama frecuencia relativa acumulada de un valor de una variable estadística a la suma de las frecuencias relativas de todos los valores menores o iguales que él.
Ejemplo 10. La frecuencia relativa del 5 es 4/17 y la relativa acumulada del 2 es 3/17.
. Representación de datos: Tablas.
Las dos formas más comunes de representar los datos son las tablas y los gráficos.
Tablas estadísticas
Las tablas estadísticas consisten en masas estructuradas de datos.
Para la construcción de tablas de datos cuantitativos pueden tratarse éstos individualmente o agrupándolos en clases
Tratamiento individual
Para variable discreta, o que siendo continua tengamos pocos datos. Lo vemos con un ejemplo.
Ejemplo 11. Las notas de los 20 alumnos de una clase son:
4, 3, 3, 5, 6, 7, 9, 0, 5, 4, 9, 10, 2, 7, 2, 2, 5, 6, 5, 0
Vamos a calcular una tabla:
|
Variable |
Frecuencias |
absolutas |
Frecuencias relativas |
|
|
estadística xi |
puntuales ni |
acumuladas Ni |
puntuales fi |
acumuladas Fi |
|
0 2 3 4 5 7 9 |
2 3 2 2 5 3 3 |
2 5 7 9 14 17 20 |
1/10 3/20 1/10 1/10 1/4 3/20 3/20 |
1/10 5/20=1/4 7/20 9/20 14/20=7/10 17/20 20/20=1 |
Ejercicio 1. En un Instituto hay matriculados 2200 alumnos que se distribuyen por edades en la forma siguiente: 215 de 14 años, 437 de 15, 421 de 16, 396 de 17, 512 de 18, 124 de 19 y 95 de 20. Formar la tabla de distribución y de frecuencias, que incluya frecuencias acumuladas.
Tratamiento por clases
Cuando en la población o muestra que estudiamos existen muchos valores diferentes, es conveniente, aún a costa de perder algo de información, dividir el intervalo de variación en una serie de subintervalos que cubran el total; a cada uno de ellos se le llama una clase, a sus extremos, extremos de clase, al punto medio de cada clase, marca de clase y a la diferencia entre sus extremos, amplitud de la clase.
Lo vemos con un ejemplo.
Ejemplo 12. Se ha pasado un test de 79 preguntas a 600 personas. El número de respuestas correctas se refleja en la siguiente tabla:
|
intervalos |
mi |
f. abs. puntual |
f. abs. acumulada |
f. rel. puntual |
f. rel. acumulado |
|
[0, 10) [10, 20) [20. 30) [30, 40) [40, 50) [50, 60) [60, 70) [70, 80) |
5 15 25 35 45 55 65 75 |
40 60 75 90 105 85 80 65 |
40 100 175 265 370 455 535 600 |
1/15 1/10 1/8 3/20 7/40 17/120 2/15 13/120 |
1/15 1/6 7/24 53/120 37/60 91/120 107/120 1 |
|
|
|
600 |
|
1 |
|
Ejemplo 13. En una Caja de Reclutamiento se toma una muestra de tamaño 30 de los pesos de los mozos correspondientes a un cierto reemplazo, obteniéndose los siguientes datos medidos en kg:
71.9, 63.9, 62.3, 72.5, 78.0, 70.7, 71.4, 60.5, 60.9, 68.2, 88.5, 76.1, 82.1, 63.7, 79.8, 67.5, 50.1, 69.5, 66.1, 47.3, 72.1, 59.8, 93.7, 80.7, 61.2, 64.3, 53.7, 74.7, 96.3, 73.2.
Construir una tabla de frecuencias agrupando los datos en clases de la misma amplitud.
Solución
Si bien no es estrictamente necesario, en general, es conveniente ordenar los datos de menor a mayor. A continuación se presenta la misma muestra ordenada:
47.3, 50.1, 53.7, 59.8, 60.5, 60.9, 61.2, 62.3, 63.7, 63.9, 64.3, 66.1, 67.5, 68.2, 69.5, 70.7, 71.4, 71.9, 72.1, 72.5, 73.2, 74.7, 76.1, 78.0, 79.8, 80.7, 82.1, 88.5, 93.7, 96.3.
Como los valores extremos son 47.3 y 96.3 y el número de clases aconsejado para estos datos es 6 (aplicando la fórmula de Sturges), tomaremos 6 intervalos de amplitud 10, la tabla queda estructurada de la siguiente manera:
|
clases |
Marcas de clase |
frecuencias absolutas de clase ½acumuladas |
Frecuencias relativas de clase ½acumuladas |
||
|
45 -55 55 -65 65 -75 75 -85 85 -95 95 -105 |
50 60 70 80 90 100 |
3 8 11 5 2 1 |
3 11 22 27 29 30 |
0.1 0.266 0.366 0.166 0.066 0.033 |
0.1 0.366 0.733 0.900 0.966 1 |
30 0.997»1
Ejercicio 2. El número de personas que viven en cada uno de los portales de una gran barriada es:: 63, 58, 70, 47, 120, 76, 80, 59, 80, 70, 63, 77, 104, 97, 78, 90, 112, 88, 67, 58, 87, 94, 100, 74, 55, 80, 75, 49, 98, 67, 84, 73, 95, 121, 58, 71, 66, 87, 76, 56, 77, 82, 93, 102, 56, 46, 78, 67, 65, 95, 69, 90, 58, 76, 54, 76, 98, 49, 87, 69, 80, 64, 65, 56, 69, 68, 99, 106.
Construye una tabla de frecuencias[2].
Series cronológicas
Se Llaman series cronológicas a unas tablas estadísticas que recogen observaciones hechas a lo largo del tiempo, normalmente a intervalos iguales. Es por tanto una serie estadística en que la variable independiente es el tiempo.
Ejemplo 14. El número de médicos colegiados en España en el período de 1984 - 1992:
|
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
|
99730 |
107503 |
119890 |
123543 |
129897 |
138967 |
147978 |
152943 |
156748 |
Ejercicio 3. La producción editorial española de libros de sociología y Estadística, en los años que se indica es:
|
Años |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
|
nº |
345 |
487 |
589 |
376 |
479 |
652 |
741 |
Hacer una tabla de frecuencias absolutas y relativas puntuales. Expresar la relativa en porcentajes.
Representación de datos: Gráficos.
Los gráficos no son más que traducciones a un dibujo del contenido de las tablas. La finalidad de los gráficos estadísticos es que la información esté al alcance de personas no expertas, que entre por los ojos. Los hay de muy diversos tipos pero todos son muy fáciles de interpretar.
Variables cualitativas
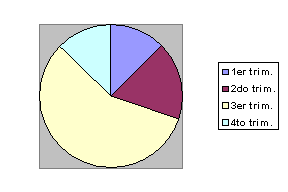 |
Los más usados son los diagramas de rectángulos ( de barras) y los de sectores.
Ejercicio
4. El censo, en miles de cabezas, del ganado en el territorio
español, en 1994 fue:
|
Ganado |
Número de cabezas |
|
Bovino Ovino Caprino Porcino Caballar Mular Asnar |
5300 18047 2601 12308 264 153 164 |
Dibujar un diagrama de sectores y otro de rectángulos.
Variables cuantitativas.
Distinguiremos entre variable discreta o continua.
Tratamiento individual
Para el tratamiento individual los medios de representación más utilizados son el gráfico (o diagrama) de barras, el polígono de frecuencias y los gráficos acumulativos.
Diagrama de barras: Se asocia a una tabla de frecuencias ya sea absoluta o relativa.
Sobre un eje horizontal se representan los valores discretos que toman los datos y sobre cada uno de ellos se coloca una barra vertical (o un rectángulo) de longitud (altura) proporcional a la frecuencia.
Ejemplo 15. Vamos a hacer un diagrama de barras de frecuencias absolutas para el ejemplo 6.
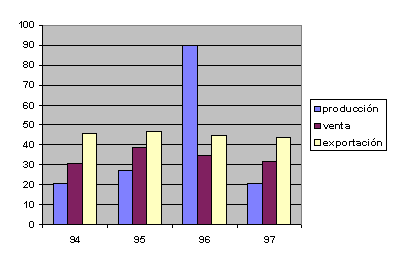
En ocasiones se superponen dos o más diagramas para comparar datos:
Ejemplo 16: Producción y venta de automóviles en España:
Polígono de frecuencias: Como el anterior se asocia a una tabla de frecuencias.
Se representan en un sistema cartesiano los puntos aislados y luego se unen por medio de segmentos (poligonal). Se usa sobre todo para frecuencias acumuladas (figura 1).
También para series cronológicas.
Ejercicio 5. La esperanza de vida al nacimiento ha evolucionado desde 1900, como se refleja en la tabla siguiente:
|
Años |
1900 |
1910 |
1920 |
1930 |
1940 |
1950 |
1960 |
1970 |
1980 |
|
Varones |
33,9 |
40,9 |
40,3 |
48,3 |
47,1 |
59,8 |
67,4 |
69,6 |
72,6 |
|
Mujeres |
35,7 |
42,6 |
42,1 |
51,6 |
53,2 |
64,3 |
72,2 |
75,1 |
78,6 |
Dibujar los polígonos de frecuencias superpuestos para poder compararlos.
Gráficos acumulativos: Se construye a partir del mismo eje horizontal del gráfico de barras, llevando sobre cada valor discreto una vertical de longitud proporcional a la frecuencia acumulada, absoluta o relativa, de dicho valor. Se suele completar el gráfico dándole forma de una escalera de peldaños horizontales.
Ejemplo 16. Gráfico de barras acumulativo
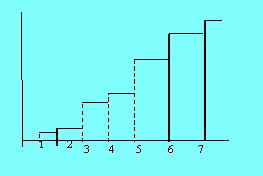
Tratamiento por clases
Cuando las variables son continuas, o discretas agrupadas, los gráficos que más se utilizan son: el histograma de frecuencias y los polígonos de frecuencias (absolutas o relativas)
Histogramas de frecuencias. Sobre el eje de abscisas se marcan los extremos de las sucesivas clases y con base en cada clase se dibuja un rectángulo de altura proporcional a la frecuencia (absoluta o relativa) observada en dicha clase.
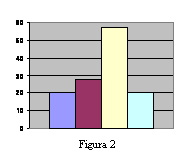 Histogramas
de frecuencias. Sobre el eje de abscisas se marcan los extremos de las
sucesivas clases y con base en cada clase se dibuja un rectángulo de altura proporcional
a la frecuencia (absoluta o relativa) observada en dicha clase.
Histogramas
de frecuencias. Sobre el eje de abscisas se marcan los extremos de las
sucesivas clases y con base en cada clase se dibuja un rectángulo de altura proporcional
a la frecuencia (absoluta o relativa) observada en dicha clase.
 |
Ejercicio 6. En la siguiente tabla se presenta la distribución por edades del número de muertes registradas en España (datos hasta el 30-9-94) a causa del SIDA.
|
Edad en años |
<3 |
3-9 |
10-12 |
13-14 |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-49 |
50-59 |
60-69 |
|
Nº de muertes |
411 |
171 |
35 |
31 |
247 |
2888 |
8576 |
7640 |
3292 |
2552 |
909 |
544 |
a) Construye la tabla de frecuencias relativas agrupando los datos en las siguientes categorías de edad: 0-9, 10-19, 20-29, 30-39, 40-49, 50-59 y 60-69 años.
b) Representa gráficamente la información obtenida en el apartado a) mediante un histograma,
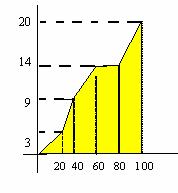
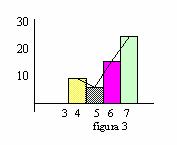
Polígono de frecuencias. Se asocia a cada clase un punto del plano cartesiano, de abscisa el valor de la marca de clase y de ordenada la frecuencia observada en dicha clase. Uniendo los puntos resulta una línea quebrada que se denomina polígono de frecuencias (figura 3)
Polígono de frecuencias acumuladas.
Partiendo del valor cero en el extremo izquierdo de la primera clase, el polígono acumulado va tomando en los sucesivos extremos derechos de las clases un valor igual a la frecuencia acumulada. Uniendo los puntos así obtenidos resulta el polígono acumulativo de frecuencias (figura 4).
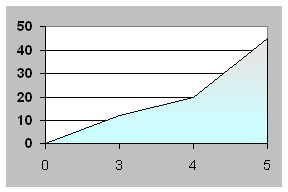 |
figura 4
Ejercicio 7. Los jugadores de un determinado equipo de baloncesto se clasifican, por altura, según la tabla siguiente:
|
Altura |
1,70-175 |
1,75-1,80 |
1,80-185 |
185-190 |
1,90-1,95 |
1,95-2,00 |
|
Nº de jugadores |
1 |
3 |
4 |
8 |
5 |
2 |
Dibujar el polígono de frecuencias absolutas acumulativo.
Parmetros estadísticos.
Las tablas estadísticas son una forma organizada de dar toda la información, todos los datos de que disponemos.
Con las gráficas estadísticas se pierde algo de información, pero el mensaje “entra por los ojos”, que es lo que se pretende.
En cualquiera de los dos casos, la cantidad de datos que se dan es excesiva para que sea operativo, por ejemplo para la comparación con otras distribuciones.
Por ello se definen los parámetros estadísticos, que nos van a servir para resumir en números aspectos relevantes de la distribución, que puedan dar una idea de la misma o permitir compararlas con otras.
Clases de parámetros estadísticos
¨ Medidas de centralización: media (ya conocida), moda (el valor que se presenta con más frecuencia) y mediana (el valor del individuo que ocuparía el lugar central sí se colocaran ordenados de menor a mayor). Tienen como misión representar con un número a la serie estadística bajo el punto de vista de su posición.
Fórmula de la media: 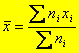
¨ Medidas de dispersión: rango o recorrido (diferencia entre los valores extremos), desviación media, varianza, desviación típica. Sirven para medir el grado de alejamiento de los datos respecto de una medida central.(la media)
La desviación media se
calcula así: 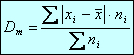
La varianza ese calcula así: 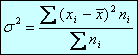 =
=![]()
La desviación típica es la raíz cuadrada de la varianza.
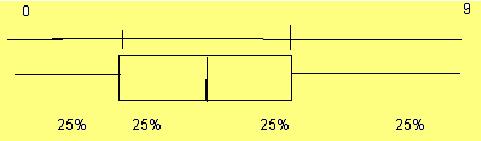
¨ Medidas de posición: cuartiles, deciles, centiles o percentiles. Señalan la situación de algunos valores importantes de la distribución.
En la ordenación que se hizo para la mediana se llaman cuartiles primero, segundo y tercero a los que superan exactamente al 25%, 50% y 75% de los valores. El segundo cuartil es la mediana. Para su obtención se usan los diagramas de cajas
Para el cálculo práctico de muchos parámetros estadísticos se utilizan tablas que facilitan dichos cálculos. Utilizaremos dos tipos de tablas que llamamos Tabla I y Tabla II:
TABLA 1
|
|
|
|
|
|
|
|
TABLA 2
|
|
|
|
|
|
Ejemplo 17. Construir la tabla 1 con los datos del ejemplo 11
|
xi |
ni |
|
|
|
|
|
|
0 2 3 4 5 7 9 |
2 3 2 2 5 3 3 |
0 6 6 8 25 21 27 |
4,65 2,65 1,65 0,65 0,35 2,35 4,35 |
9,30 7,95 3,30 1,30 1,75 7,05 13,05 |
21,62 7,02 2,72 0,42 0,12 5,52 18,92 |
43,24 21,06 5,44 0,84 0,60 16,56 56,76 |
20 93 la media es 93/20=4,65
Ejemplo 18. Construir la tabla 2 con los datos del ejemplo 13.
|
clases |
Marcas de clase xi |
frecuencia ni |
|
|
|
|
|
45 -55 55 -65 65 -75 75 -85 85 -95 95 -105 |
50 60 70 80 90 100 |
3 8 11 5 2 1 |
150 480 770 400 180 100 |
2500 3600 4900 6400 8100 10000 |
7500 28800 53900 32000 16200 10000 |
|
Ejemplo 19. a) Hallar la media y la varianza de la variable cuyos valores y frecuencias absolutas vienen dadas en la tabla adjunta
|
Valores de la variable |
3 |
5 |
4 |
2 |
0 |
8 |
7 |
|
frecuencias |
1 |
3 |
4 |
1 |
3 |
1 |
2 |
b) Representar gráficamente los datos en un diagrama de barras.