EJERCICIOS DE MATEMÁTICAS 3º ESO (ANEXO)[C1]
1. Calcula el valor de k para que la división de P(x) entre Q(x) dé exacta:
a) P(x) = ) x3 -11x2 +k.x -24, Q(x) = (x-1)
b) P(x) = x4 -11x3 +33x2 –k x -54; Q(x) = (x +1)
2. Calcula el valor de k, para que el resto de la división de x4 –k x3 +33x2 – x -54 entre x +2 nos dé 25.
3. Descomponer en factores los polinomios P(x) y Q(x) y hallar su M .C .D y M . C . M
a) P(x) = x3 -1 y Q(x) = x2 -2x +1
4. Resuelve las siguientes ecuaciones bicuadradas:
a) x4 –3x2+2=0
b) x4-13x2+36=0
Solución
Hacemos x2 =t
t2-13t+36=0,
ecuación de segundo grado que se resuelve con la fórmula , 
x =9= t2
o x =4= t2, de donde , t =
c) x4-1=0
5. Resuelve las siguientes ecuaciones irracionales y comprueba las soluciones:
a) 
b) 
c) 
Solución
x2-2x+ 1= 2x-3
x2-4x+4=0 luego x =2
Comprobación
Sí es solución
d) 
e) 
6. Resuelve las siguientes ecuaciones:
a) x3 -11x2 +34x -24=0
b) x4 -11x3 +33x2 -9x -54=0
c) x4 –x3-16x2-20x = 0
7. Resuelve los siguientes sistemas[C2]:
a) 
b) 
c)
8. La base de un rectángulo es 10cm más larga que la altura. Su área mide 600m2. Calcular las dimensiones del rectángulo.
9. Dos números son tales que el mayor menos la raíz cuadrada del menor es 22 y la suma de los números es 34. ¿Cuáles son los números.
10. El área de una lámina de plata es 48cm2, y su longitud es 4/3 de su anchura. Halla su longitud y su anchura.
ACTIVIDADES GEOMETRÍA 3º ESO
2. POLÍGONOS
ACTIVIDADES DE MATEMÁTICAS 3º ESO
1. Dada la función f que asocia a cada número su triple:
a) Escribir la expresión de la función.
b) Calcular f(-1), f(0) y f(2)
c) Calcula su dominio y recorrido.
2. Halla el dominio de las funciones:
a) f(x)= x3-3x+1
b) f(x)= 
c) 
3. Estudia la simetría de las siguientes funciones, respecto del eje de ordenadas o respecto el origen:
a) f(x)= x2+1; b) f(x)=x3; c) f(x)=x3+1
4. Dibuja la gráfica que indica el coste de una carrera de taxi de 3Km, sabiendo que cada 300 m cuesta 0,50 €, y la bajada de bandera inicial 1 €. ¿Es creciente la función? ¿Es continua?
5. Las curvas de oferta y de demanda de cierto tipo de ordenadores son, respectivamente:
y =2x- 1000
y = 0,5x +2000
en donde x es el precio en euros de los aparatos e y el número de aparatos ofertados o demandados. Hallar el punto de equilibrio.
Solución
Se llama punto de equilibrio a aquél en que coinciden la oferta y la demanda. Es decir donde se cortan las dos curvas.
Para hallarle analíticamente se resuelve el sistema que forman las dos curvas, en nuestro caso:
y =2x- 1000
y = 0,5x +2000
Lo hacemos por igualación:
2x-1000=0,5x+2000
1,5x=3000,
despejando x =2000 y sustituyendo en la 1ª ecuación, por ejemplo,
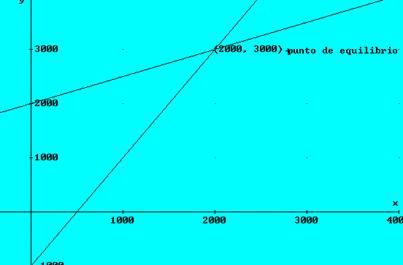
y =4000 -1000 =3000. el punto de equilibrio es el (2000, 3000)
Gráficamente:
6. Estudia la continuidad de las siguientes funciones:
a)
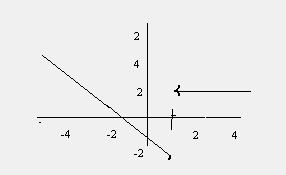
b)
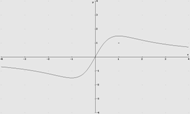
7. Dada la función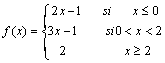 
a) Representación gráfica.
b) Clasifica los puntos de discontinuidad.
8. Halla la tasa de variación de la función f(x)=x2+1 en los intervalos [0, 3], [3, 5] y [-3, -1]. ¿Es constante la tasa de variación?
ACTIVIDADES DE REFUERZO (Funciones y gráficas)
1. 1 Representa las siguientes rectas, señalando los puntos de corte con los ejes:
a) y = 2-x; b) x +y =- 1; c) 2x+ 3y=6
1.2. Indica sus pendientes.
Solución 1.2
Las pendientes son a) -1, b) -1, c) -2/3
2. Calcula los puntos de corte con los ejes y el vértice de las siguientes parábolas:
a) y = -x2+9; b) y = x2-2x-3, c) y = x2-2x+3
Haz su representación gráfica.
3. Resuelve analítica y gráficamente los sistemas:
a) 
b) 
Solución
b)Analítica
como en la primera ecuación la y está despejada se sustituye este valor en la segunda ecuación:
x + x2-2x-3=-3 
x2 –x =0 x(x-1)=0
x
=0, x =1. sustituyendo los valores de x en la primera ecuación obtenemos los
valores de y, que son y =-3, y = -4
Las soluciones son por tanto el (0, -3) y el (1, -4)
b) Gráfica
Dibujamos la recta x +y =-3 utilizando los puntos de corte con los ejes, que son (0, -3) y (-3, 0)
Para la parábola, y =x2 -2x-3, consideramos los puntos de corte con los ejes y el vértice:
Punto de corte con el eje OY 
es decir el punto (0,
-3)
Puntos de corte don el eje OX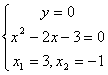 
es decir los puntos (3,
0) y (-1, 0)
Vértice: abscisa 
, ordenada 
El vértice es el punto V(1, -4), la gráfica:
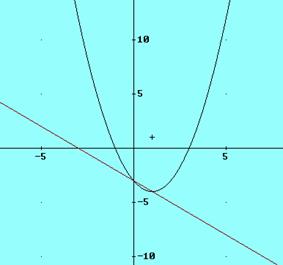
4. Cierta entidad financiera lanza al mercado un plan de inversión cuya rentabilidad, R(x), viene dada en función de la cantidad que se invierta x, por medio de la siguiente expresión:
R(x)= -0,001x2+0,5x+2,5
a) Deducir razonadamente la cantidad de dinero que le conviene invertir a un cliente en dicho plan .
b) ¿Qué cantidad obtendría?
Indicación : Que tipo de función es R(x)?
5. La velocidad (en m./sg.) que alcanza cierto atleta en una carrera de 200 metros viene dado en función del espacio recorrido, x, por la siguiente expresión:
f(x) =-0´00055 x (x-300)
Deducir de forma razonada:
¿Qué distancia ha recorrido el atleta cuando alcanza su velocidad máxima?¿cuál es ésta velocidad?
Solución
La función que nos da la velocidad es cuadrática (f(x) =-0´00055 x (x-300)= -0,00055x2+0,165x)
La gráfica es una parábola y el vértice es el punto más alto (el coeficiente de x2 es negativo) por lo tanto el máximo se encontrará en la abscisa del vértice de la parábola.
Entonces :
xv =
m es la distancia que ha recorrido
cuando alcanza la velocidad máxima.
La velocidad máxima es f(150) (calcular e valor sustituyendo la x por 150)
6.Dada la función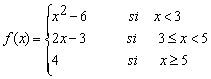 
Representación gráfica.
Estudia los puntos en que f es discontinua.
7. Halla la tasa de variación media de la función f(x) =3-x2 en el intervalo [0, 2].
8. En nuestra ciudad la oferta (S) y la demanda (D) de un producto cuyo precio es de x € vienen dadas por las siguientes ecuaciones:
S(x)= -900 +18x; D(x)= 2400 -12x
Calcula gráficamente el punto de equilibrio. Hazlo luego analíticamente.
Cuaderno de actividades 3º ESO Cuaderno actividades 4º ESO
