3º Parte: Ecuaciones y Sistemas
Igualdades, identidades, ecuaciones
Una igualdad, (=), es una relación de equivalencia[1] entre dos expresiones, numéricas o literales, que se cumple para algún, alguno o todos los valores. Cada una de las expresiones recibe el nombre de miembro.
|
igualdad
una expresión = otra expresión
primer miembro segundo miembro
|
· Si la igualdad se cumple entre números se denomina identidad numérica.
Ejemplo 1: 2 +4 +5 = 1 +10
· Una identidad literal es una igualdad que se cumple para todos los valores.
Ejemplo 2: Las Identidades Notables
Cuadrado de una suma ![]()
Cuadrado de una diferencia ![]()
Diferencia de cuadrados ![]()
· Cuando la igualdad se convierte en identidad numérica sólo para determinados valores se la llama ecuación. A las letras se les llama indeterminadas o incógnitas.
Ejemplo 3: a) 3x+2 =0 es una ecuación con una incógnita.; b)3x +2y =1 es una ecuación con dos incógnitas.
Al valor, o valores, que convierten la ecuación en identidad numérica se les llama solución (o raíz) de la misma.
Ejemplo 4. Una solución de la ecuación del ejemplo 3 es x =-2/3 .
Ejercicio 1. Encuentra 2 soluciones de la ecuación 3x-2y-1=0
Resolver una ecuación en encontrar todas su soluciones o llegar a la conclusión de que no tiene ninguna.
Ejemplo 5. a) x2-1=0 tiene dos soluciones, x =1 y x =-1
b) x2 + 1=0 es una ecuación sin soluciones en R.
c) 2x +3y = 0 tiene infinitas soluciones, (0,0), (-3,2), (3, -2)....
Ecuaciones equivalentes
Dos ecuaciones son equivalentes cuando admiten la mismas soluciones. Se cumple:
![]() Si se suma o resta un mismo número a los dos miembros de una
ecuación, se obtiene una ecuación equivalente a la primera.
Si se suma o resta un mismo número a los dos miembros de una
ecuación, se obtiene una ecuación equivalente a la primera.
![]() Si se multiplican o dividen los dos miembros de una ecuación por
un mismo número distinto de cero se obtiene una
ecuación equivalente a la primera.
Si se multiplican o dividen los dos miembros de una ecuación por
un mismo número distinto de cero se obtiene una
ecuación equivalente a la primera.
Trasposición de términos. Aplicando las reglas anteriores deducimos dos reglas prácticas:
![]() Si un número aparece en un miembro sumando, se le puede
pasar al otro miembro restando. Si esta restando pasará sumando.
Si un número aparece en un miembro sumando, se le puede
pasar al otro miembro restando. Si esta restando pasará sumando.
![]() De igual manera si está multiplicando pasa dividiendo
y al revés.
De igual manera si está multiplicando pasa dividiendo
y al revés.
Esto se llama trasponer términos.
Ejemplo 6: La ecuación 5x - 1 = 2x -3 se puede escribir 3x + 2 = 0, trasponiendo términos.
Nota : El segundo miembro de la ecuación se puede considerar siempre que es 0.
Ecuaciones de primer grado
La forma general de esta ecuación
es a x +b =0 con a![]() 0
0
Trasponiendo y dividiendo por a
se llega a ![]() .
.
Solución que siempre existe y es única.
Ejemplo 7. a) 3x +2 =0 Þ ![]()
b) 7x + 2 = 2x -3 , si trasponemos términos, nos queda 7x –2x = -2 –3
Luego 5x = -5 de donde x = -1
Ecuaciones de segundo grado
La forma general de una ecuación de 2º grado es: ![]() , donde a
, donde a![]()
La solución de esta ecuación general viene dada por la fórmula:
![]()
Ejemplo 8. ![]()
![]() =
=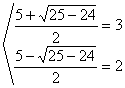
Observación. A D =![]() se llama discriminante de la ecuación de 2º y se
verifica:
se llama discriminante de la ecuación de 2º y se
verifica:
Si D>0 la ecuación tiene dos soluciones conjugadas
Si D =0 la ecuación tiene una única solución (doble)
Si D <0 la ecuación no tiene ninguna solución real.
Ecuaciones incompletas
![]() Si c =0 la ecuación se reduce a
Si c =0 la ecuación se reduce a ![]() y sacando factor común x
se tiene:
y sacando factor común x
se tiene:
x(ax +b) =0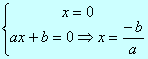
Este tipo de ecuación siempre tiene dos soluciones.
Ejemplo 9. 3x2-5x=0 x(3x-5)=0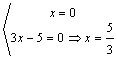
![]() Si b =0 la ecuación queda
Si b =0 la ecuación queda ![]() de donde
de donde ![]()
Puede tener dos soluciones opuestas o ninguna solución, dependiendo de que
El radicando sea o no positivo.
Ejemplo 10. 2 x2-![]() =0; 2 x2=
=0; 2 x2=![]() Þ
Þ ![]() (dos
soluciones)
(dos
soluciones)
Ejemplo 11. 3x2+1 =0 ![]() (no
tiene ninguna solución)
(no
tiene ninguna solución)
Resolución “práctica” de una ecuación
Lo estudiamos con un ejemplo
Ejemplo 12. ![]()
Para resolver la ecuación seguiremos el siguiente orden.
1º Quitar denominadores
Al multiplicar los dos miembros de una ecuación por el mínimo común múltiplo de sus denominadores, se obtiene otra ecuación equivalente a la primera, pero sin denominadores.
Multiplicamos los dos miembros de la igualdad por 6, que es el m.c.m. de los denominadores.
Nos queda 3(2x-3) -2(5x-1) =6
2º Quitar paréntesis
Se efectuarán las operaciones indicadas, utilizando la propiedad distributiva.
Quitando paréntesis 6x-9 –10x+2=6
3º Trasnposición de términos
Se disponen todos los términos que llevan x en un miembro y los demás en el otro.
Trasponiendo términos 6x –10x = 9 - 2 + 6
4º Reducción de términos semejantes
De este modo cada miembro de la ecuación queda con un solo término:
-4x = 13
5º. Despejar la incógnita
Se
dividirá ambos miembros por el coeficiente de la incógnita (se puede hacer
siempre que sea a![]() 0)
0)
![]()
Observación. Dependiendo de la ecuación a resolver puede ocurrir que alguno de los pasos sea innecesario, se omite y se pasa al siguiente.
![]() Ecuaciones de primer grado
Ecuaciones de primer grado
Resuelve
1) ![]()
2)![]()
3) ![]()
4) ![]()
5) ![]()
7) ![]()
8) ![]()
9) ![]()
Solución.
Multiplicamos los dos miembros por 8 (es el m.c.m. de los denominadores)
(2x-4)2 = 40 +4x(x +1)
4x2 –16x +16 = 40 + 4x2 +4x
4x2 –16x +16 =40 +4x2 +4x
Reduciendo términos semejantes:
... 16x-4x=
40- 16 -20x =24 ![]() = -1,2
= -1,2
10) ![]()
![]() Ecuaciones de segundo grado
Ecuaciones de segundo grado
Resuelve las siguiente ecuaciones indicando si son completas o no:
1) 3x2+ 2x=0
2) 5x2-3=0
3) x2-4x+2=0
4) 2x2+ x-1=0
5) 3 x2-![]() =0 Þ 3x2 =
=0 Þ 3x2 =![]() Þ x2=
Þ x2=![]() Þ x =
Þ x =![]()
6) –x2 + 4 =0
8) 4x2 –4x +1 =0
9) –x2 +6x-5=0
10) –6x2 +5x-1=0
11) (5x-4)(2x+3) =5
12) 30 + 9x – 3x2 =0
13)
![]()
Solución.
Multiplicamos por el M.C.M de los denominadores, que es 2(2 +x):
(2 +x)(2-x) +4.2 =2(2 +x)
4 –x2 +8 =4 + 2x,
agrupando términos y organizando la ecuación
0 = x2 +2x
–8 Þ 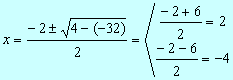
14) ![]()
15) ![]()
16) ![]()
***[C1]Aplicaciones de las ecuaciones de 2º grado
![]() Descomposición en factores del trinomio de 2º grado.
Descomposición en factores del trinomio de 2º grado.
Ejemplo 13.La ecuación x2 –5x +6= 0 tiene dos raíces r1=3 y r2= 2 (comprobarlo).
Entonces se puede descomponer en producto de (x-3) por (x-2). Es decir:
x2 –5x +6 = (x-3)(x-2).
Ejercicios
Determina los factores de los siguientes trinomios de 2º grado
1) x2-16
2) x2-13x+36
3) 4 -x2
4) 2x2+17+21
5) 2x2-5x+7
6) 3x2- 0,75
7) –x2 +5x-6
4) Solución
![]() =
=![]()
Luego 2x2+17+21= 2(x +1)(x +7)
![]() Resolución de ecuaciones irracionales.
Resolución de ecuaciones irracionales.
Ejemplo 14. ![]()
Se procede de la forma siguiente:
1) Se aísla la raíz:
![]()
2) Se elevan al cuadrado ambos miembros de la igualdad:
4(x-1)=(4-x)2 Þ 4x-4 = 16-8x +x2
3) Se resuelve a ecuación de 2º grado que resulta
x2-12x +20 =0 x =10 y x =2 (comprobarlo)
4) Se comprueban las soluciones
Si x =10
![]() 16 - 4= 0 Falso, no es
solución
16 - 4= 0 Falso, no es
solución
Si x =2
![]() 4 - 4=0 Cierto, si es solución.
4 - 4=0 Cierto, si es solución.
Ejercicios
Resuelve las siguientes ecuaciones y comprueba las soluciones:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
Solución.
Aislamos una de las raíces: ![]()
Elevamos al cuadrado (![]()
![]()
Volvemos a aislar la raíz que nos queda
![]()
Elevamos al cuadrado
144(2x-1)=x2 +62x+961
288x -144 = x2 +62x +961
Es decir:
x2 –226x +1105 =0
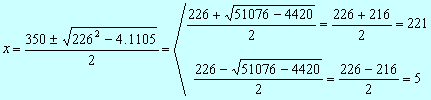
Comprobamos las soluciones:
x =221 no es solución pues
![]()
![]()
x =5 sí es solución
![]()
3=3
7) ![]()
![]() Ecuaciones bicuadradas
Ecuaciones bicuadradas
Ejemplo 15. La ecuación x4 – 5x2 +6=0 es bicuadrada (es de 4º grado sin potencias impares).
Para resolverla se procede así:
Se hace un cambio de incógnita
x2= y
con lo cual x4 = y2
Sustituyendo en la ecuación: y2-5y+6=0
que sí es de 2º grado y podemos aplicar la fórmula: 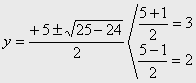
Sustituyendo los valores en la
expresión x2= y , x =![]() obtenemos:
obtenemos:
![]() y
y
![]()
En este caso la ecuación tiene 4 soluciones.
Ejercicios
Resuelve:
1) x4 –3x2+2
2) x4-13x2+36
3) x4-1
4) x4+ 4x2 =0
Solución.
Como es incompleta, .al igual que en las de segundo grado, sacamos factor común
x2(x2 +4) =0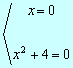 que tiene sólo la solución (doble) x =0
que tiene sólo la solución (doble) x =0
5) x4-9x2=0
6) 3x4 –5x2+2=0
7) x4+ x2+1=0
8) ![]()
Sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales.
Ejemplo 16: ![]() es un sistema de 2 ecuaciones con dos incógnitas
es un sistema de 2 ecuaciones con dos incógnitas
Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.
Hay tres métodos para resolverlos:
![]() Sustitución
Sustitución
Ejemplo 17.
![]()
En la 2ª ecuación despejamos la y y la sustituimos en 1ª ecuación
y =3x; 2x +3(3x) =1Þ 11x =1
Þ x =1/11
Una vez encontrado el valor de una de las incógnitas se sustituye (y =3x) para encontrar el valor de la otra incógnita: y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de, al menos, una de las incógnitas es 1.
![]() Igualación
Igualación
Ejemplo 18. ![]()
Despejamos la misma incógnita en
las dos ecuaciones![]() ; y =3x.
; y =3x.
Igualando ![]() Þ 1-2x =9x Þ 1= 11x Þ x =1/11
Þ 1-2x =9x Þ 1= 11x Þ x =1/11
Ahora para obtener el valor de la y se procede como en el caso anterior, es decir se sustituye el valor hallado en la ecuación que más convenga ( en este caso en y =3x). y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de una de las incógnitas es igual en las dos ecuaciones.
![]() Reducción
Reducción
Ejemplo 19. ![]()
Multiplicamos la 1ª ecuación por 2 y la 2ª por 3. (De esta forma el coeficiente de y en las dos ecuaciones es el mismo, el m.c.m.
Resulta: ![]() Þ
Þ ![]()
Sumando obtenemos 13 x =2 Þ![]()
Sustituyendo el valor encontrado de x en la segunda ecuación:
![]() y =3/13
y =3/13
Observación. Este método es muy adecuado en todos los casos.
Nota. A veces es más cómodo usar la reducción dos veces para encontrar el valor de la otra incógnita. (Ver ejercicio resuelto)
Ejercicios
Resuelve los siguientes sistemas por el método que creas más adecuado:
1) ![]()
2) ![]()
3) ![]()
4)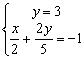
5) ![]()
6) 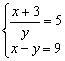
7)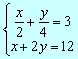
Solución
Para quitar los denominadores multiplicamos por 4 la
1ª ecuación Þ![]()
Le resolvemos por reducción doble.
Multiplicamos la 2ª ecuación por –2 Þ![]()
Sumando las dos ecuaciones obtenemos una equivalente: -3y = -12Þy =4
Para encontrar el valor de x, eliminamos la y, para ello multiplicando la 1ª por -2
![]() sumando –3x= -12Þ x
=4
sumando –3x= -12Þ x
=4
8) ![]()
Problemas de aplicación
1) Calcula dos número cuya suma sea 8 y su producto 12.
2) La suma de dos número es 65 y su diferencia 23. Halla los números
3) La diferencia de dos números es 1/6. El triple del mayor menos el doble del menor es 1. Halla dichos números.
Sistemas de ecuaciones de 2º grado
Son aquellos en que al menos una de las ecuaciones es de 2º grado. Veremos con un ejemplo como proceder para obtener las soluciones
Ejemplo 20. Sea el
sistema ![]()
En la 2ª ecuación despejamos la y, y la sustituimos en la 1ª
y = 2x-4Þ 2x2+(2x –4)2=22
2x2 +4x2 –16x +16=22; 6x2-16x-6=0,
Simplificando por 2 obtenemos:3x2-8x-3=0, que es una ecuación de 2º grado completa:
![]() =
=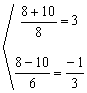
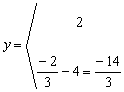
Ejercicios
Resuelve los siguientes sistemas:
1) ![]()
2) ![]()
3)![]()
Para resolver un problema es conveniente realizar cuatro fases[2]:
1ª. Comprender el problema.
Hay que leer el problema hasta familiarizarse con él y que podamos contestar, sin dudar, a las siguientes preguntas:
¿Cuáles son los datos? ¿cuál es la incógnita o incógnitas? ¿son las condiciones suficientes para determinar a las incógnitas? ¿son insuficientes?.. .
2ª Concebir un plan.
Determinar la relación entre los datos y la incógnitas.
De no encontrarse una relación inmediata puedes considerar problemas auxiliares.
¿Conoces problemas relacionados con éste?
¿Podrías plantear el problema de forma diferente?
¿Puedes cambiar la incógnita o los datos o ambos si fuera necesario, de tal forma que la nueva incógnita y datos estén en una relación más sencilla?...
¿Has considerado todas las nociones esenciales del problema?
.................
Obtener finalmente un plan de solución.
Para nuestro caso:
Escribir la ecuación o ecuaciones que relacionan datos e incógnitas y analizar el sistema que forman.
3ª. Ejecutar el plan.
Resuelve el sistema por los métodos estudiados.
4ª. Examinar la solución obtenida.
Comprobar si las soluciones obtenidas son válidas y proceder en consecuencia.
Ejemplo 21.. Alejandra tiene 27 años más que su hija Carmen. Dentro de 8 años, la edad de Alejandra doblará a la de Carmen. ¿Cuántos años tiene cada una?
Solución. Sólo en este problema indicaremos con detalle las 4 fases
1º. Comprender el problema.
Es un problema con dos incógnitas y dos condiciones, luego suficientes para poder determinarlas.
Llamamos x a la edad de Alejandra e y a la de su hija.
Ordenamos los elementos del problema:
|
|
Hoy |
dentro de 8 años |
|
La madre |
x |
x + 8 |
|
La hija |
y |
y + 8 |
2º. Concebir un plan.
Escribimos las ecuaciones que relacionan los datos con las incógnitas:
x = 27 + y
x + 8 = 2(y +8)
Es un sistema lineal de dos ecuaciones con dos incógnitas. Lo resolveremos por el método de sustitución.
3º Ejecutar el plan.
x = 27 + y
Entonces:
27 + y +8 = 2(y +8) de donde 35 -16 = y Þ y = 19, x = 46
4º Examinar la solución obtenida .
La solución obtenida es factible por ser entera.
El método empleado se puede usar en problemas “similares”.
Problemas resueltos
1. La edad de una madre es siete veces la de su hija. La diferencia entre sus edades es de 24 años. ¿qué edad tienen?.
Solución
Llamamos x a la edad de la hija, luego 7x será la edad de la madre.
7x –x =24Þ 6x =24 Þ x =4
Luego edad de la hija 4 años y edad de la madre 28 años
2. Halla un número tal que su mitad más su cuarta parte más 1, sea igual al número pedido.
Solución
Llamamos x al número que buscamos, la mitad del número es x/2 y su cuarta parte x/4
Entonces: ![]()
Multiplicamos por el m.c.m. que es 4. Nos queda:
2x +x + 4 = 4x
x =4
3. Se atribuye a Pitágoras la siguiente respuesta sobre el número de sus discípulos:
- Una mitad estudia matemáticas, una cuarta parte física, una quinta parte guarda silencio, y además hay tres mujeres.
¿Cuántos discípulos tenía?
Solución
Llamamos x al número de sus discípulos.
Traduciendo a lenguaje algebraico las condiciones, se tiene:
![]()
Multiplicando por 20, que es el m.c.m. , quitamos todos los denominadores
10x +5x +4x +60 =20x
Es decir, x = 60 discípulos
4. Dos poblaciones A y B distan 25km. Un peatón sale de A hacia B a una velocidad de 4km/h. Simultáneamente sale de B hacia A otro peatón a 6km/h. Calcula el tiempo que tardan en encontrarse.
Solución
![]() A ½ B
A ½ B
25km
El espacio que recorre el peatón que sale de A es: E = v A t =4.t
El espacio que recorre el peatón que sale de B es: E = v B t = 6t
Cuando se encuentran habrán recorrido entre ambos los 25km
Por lo tanto: 4t +6t =25
10 t = 25 Þ t = 2,5 horas
Tardan en encontrarse 2 horas y media
5. En una jaula hay conejos y palomas, pueden contarse 35 cabezas y 94 patas. ¿Cuántos animales hay de cada clase?.
Solución
Llamamos x al número de conejos, y al número de palomas habrá entonces
x +y =35
Lo conejos tienen 4 patas, hay 4x patas de conejos
Las palomas 2 patas, luego tendremos 2y patas de palomas
El número de patas en total es 94 4x + 2y= 94Þ
Es decir ![]() lo resolvemos por sustitución =
y = 35 -x
lo resolvemos por sustitución =
y = 35 -x
4x +2(35 –x) = 94
4x + 70 –2x =94
2x =24 Þ x =12 y =35 –12 =23
Hay 12 conejos y 23 palomas
6. Había doble de leche en un envase que en otro. Cuando se extrajeron 15 litros de leche de ambos envases, entonces había tres veces mas leche en el primer envase que en el segundo. ¿Cuánta leche había originariamente en cada envase.
Solución.
Llamamos x al nº de litros de un envase.
En el otro envase habrá 2x litros.
Al extraer 20 litros de cada envase nos quedan
x -15 2x –15
2x –15=3(x –15) =3x – 45
x =30
En un envase había 30 litros y en el otro 60 litros
7. El hermano mayor de una familia con tres hermanos tiene 4 años más que el segundo y éste 3 más que el menor. Si entre todos tienen la edad del padre que tiene 40 años ¿qué edad tiene cada hermano ?
Solución
Llamamos x = edad del hermano menor. Entonces según las condiciones del problema:
x + 3 es la edad del hermano mediano
x +3 + 4 = x + 7 es la edad del hermano mayor
Como la suma de las edades de los hermanos es 40:
x + x +3 + x +7 = 40 Þ 3x =40 –10 =30
x =10
Por lo tanto: edades de los tres hermanos: 10 , 13 y 17 años.
8. ¿ A qué hora forman por primera vez un ángulo rcto las agujas de un reloj, a partir del mediodía.
Solución
Es un caso particular de problemas de móviles.
La velocidad del minutero es doce veces mayor que la del horario. Podemos pues representar por 12 y 1 las velocidades respectivas de las dos saetas.
Si x es el nº de divisiones que ha recorrido la aguja horaria, la minutaría formará con ella ángulo recto cuando haya recorrido x +15 divisiones
 Al
igualar los tiempos empleados por ambas, se obtiene:
Al
igualar los tiempos empleados por ambas, se obtiene:
![]() Þ 12x =x +15Þx =15/11= 1minuto 21segundos
Þ 12x =x +15Þx =15/11= 1minuto 21segundos
Se encuentran a las 12 horas 16 minutos 21 segundos
9. La edad de un padre es el cuadrado de la de su hijo. Dentro de 24 años la edad del padre será el doble de la del hijo. ¿Cuántos años tiene ahora cada uno?
Solución
Llamamos x a la edad del hijo. La del padre será x2
Dentro de 24 años el hijo tendrá x +24
Dentro de 24 años el padre tendrá x2 +24
Por lo tanto x2 +24 = 2(x +24) = 2x +48
La ecuación que resulta es de 2º grado.
x2- 2x –24=0
Por ser completa aplicamos la fórmula general:
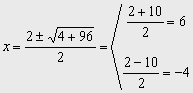
Aunque da dos soluciones, sólo la primera x =6 es válida, x =-4 no nos vale pues las edades no pueden ser negativas.
Por tanto el hijo tiene 6 años y el padre 36 años
10. Para vallar una finca rectangular de 750m2 se han utilizado 110m de cerca. Calcular las dimensiones de la cerca.
Solución
Llamamos x a la base del rectángulo, e y la altura.
Como la superficie es el producto de la base por la altura, entonces x .y =750
El perímetro es la suma de los 4 lados:
2x +2y =110
Es decir tenemos el sistema ![]() De la primera ecuación se tiene y =750/x
De la primera ecuación se tiene y =750/x
Sustituyendo en la segunda:
![]() Þ 2x2+1500
=110 x Þ 2x2-110x +1500=0
Þ 2x2+1500
=110 x Þ 2x2-110x +1500=0
De donde 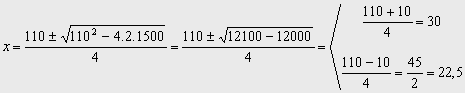
Nos da dos soluciones:
Si la base es x =30 Þ la altura es y = 750/30 =25
Si la base es x = 22,5 Þ la altura es y =750/22,5=100/3= 33,333..
Ambas válidas.
Problemas propuestos
1. Un gavilán se cruza en vuelo con lo que parece un centenar de palomas. Pero una de ellas lo saca de su error:
- No somos cien -le dice-. Si sumamos las que somos, más tantas como las que somos, más la mitad de las que somos, y la mitad de la mitad de las que somos, en es caso, contigo, gavilán, seríamos cien.
¿Cuántas palomas había en la bandada?
2. El perímetro de un jardín rectangular es de 68 m. Si el lado mayor mide 10 m. más que el lado menor. ¿Cuánto miden los lados del jardín?
3. Halla dos números positivos cuya suma es 20 y la suma de sus cuadrados 250.
4. Un ciclista sale por una carretera a 15km / h. Media hora después sale otro en su persecución a una velocidad de 20km/h. ¿Cuánto tardarán en alcanzarse?
5. Halla un número tal que su mitad más su cuarta parte más 1, sea igual al número pedido.
6. En la primera prueba de una oposición queda eliminado el 70% de los participantes. En la segunda queda eliminado el 40% de los restantes. Si el número de personas que aprobaron los dos exámenes fue 36 ¿cuántas personas se presentaron a la oposición?
7. Calcula tres números sabiendo que son consecutivos y que su suma es igual al cuádruplo del menor.
8. La base de un rectángulo es 10cm más larga que la altura. Su área mide 600m2. Calcular las dimensiones del rectángulo.
9. Un ciclista sale por una carretera a 15km / h. Media hora después sale otro en su persecución a una velocidad de 20km/h. ¿Cuánto tardarán en alcanzarse?
10. El área de una lámina de plata es 48cm2, y su longitud es 4/3 de su anchura. Halla su longitud y su anchura.
11. Halla dos números cuya suma sea 24 y su producto 135.
12. Hallar tres números impares consecutivos, tales que si al cuadrado del mayor se le restan los cuadrados de los otros dos se obtiene como resultado 7.
13. Dos números son tales que el mayor menos la raíz cuadrada del menor es 22 y la suma de los números es 34. ¿Cuáles son los números.
14. Una caja mide 5cm de altura y de ancho, cinco cm. más que de largo. Su volumen es 1500cm3. Calcular la longitud y la anchura.
15. La diagonal de un rectángulo mide 26cm y el perímetro 68cm. Hallar los lados del rectángulo.
Cuaderno
de actividades de 4º ESO![]()
