Actividades de Geometría para 4º de la ESO (opción A)
Figuras semejantes. Teorema de Tales
Razones trigonométricas. Resolución de Triángulos
Iniciación a la geometría analítica plana
1. Los lados de un triángulo A’B’C’ miden el doble que los de ABC. Si la superficie del primero es 18 dm2, ¿cuál será la superficie del segundo?
2. La razón de las áreas de dos polígonos semejantes es 25/49. ¿Cuál es la razón de sus lados?
Solución
La razón de las áreas es el cuadrado de la razón de semejanza de los lados, por tanto, le de los lados e 5/7.
3. Dos ciudades que en la realidad están a 900km, aparecen en el mapa separadas 6cm. ¿A qué escala se ha dibujado el mapa?
4. Calcula la distancia a que se encuentran 2 ciudades si en el plano están a 13 cm.
Datos: escala 1: 1800000.
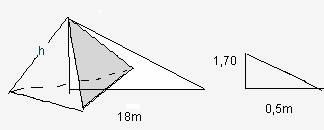
5. Calcula la altura de la pirámide sabiendo que la sombra que proyecta es de 18 m y que la sombra que proyecta Tales es de 0,5m. Nota. Tales mide 1,70 m.
Por
la semejanza de los triángulos
Þ h = 61,2m
6. La sombra de un lápiz de10cm en un determinado momento es de 25cm. ¿Cuál será en ese momento la sombra de una torre de 40m?
7. Calcula la profundidad de un pozo de diámetro 2 metros, sabiendo que alejándose 0,7m del borde, desde una altura de 1,70m vemos que la visual une el borde del pozo con la línea del fondo.
8. Cálculo de la altura del árbol de las figuras. Datos: a) longitud de la estaca (ab) 1,3 metros. b) Altura del hombre 1,80m.
a)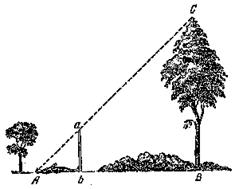 
1m 3m
b)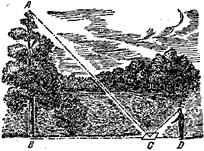 
5 1
9. Dibuja un ángulo de 40º y calcula sus razones trigonométricas.
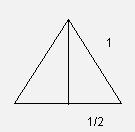10. Calcula las razones
trigonométricas del ángulo de 60º.
Solución
Dibujamos un triángulo equilátero, de lado 1,
La
altura, h, por el teorema de Pitágoras, vale 
Por
lo tanto: 
,
; 
11. Calcula, de dos formas
diferentes, el seno de 
B
12. Sabiendo que sen 30º =1/2 calcula, razonadamente, lo que vale el cos 60º.
13. Sabiendo que tg 60º =
calcula tg
30º.
14.
Sabiendo que 
,
y 
agudo
calcula las restantes razones trigonométricas.
Solución
Sustituyendo el valor del coseno en la fórmula fundamental de la Trigonometría:
, de donde 
=0,91Þ
15. Calcula
las razones trigonométricas del ángulo agudo conociendo:
a) 
; b) 
; c) 
;
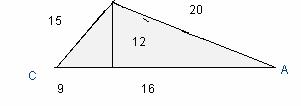
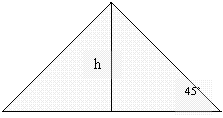16. Calcula la altura, el
lado desconocido y el área .
Solución
Se
tiene 10
=0,707Þ h =7,07 y
=1Þ
x 15-x
7,07= 15-x Þ x = 7,93 , Por T. Pitágoras: 15
y2 =x2+ h2= 62,88+49,98=112,86Þ y = 10,62 A =(15.7,07)/2=53,25 u.s.
17. Hallar el área y los ángulos del triángulo de lados 5, 7 y 10.
18[1].Calcula la altura del árbol sabiendo que el ángulo ADC es de 30º , el ACB 45º y la distancia CD =2m (problema de las tangentes)
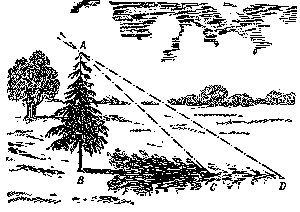
Llamamos AB =h
=0,57Þ h = 0,57.BD
=1Þ h = BC
Como BD = BC +2 se tiene
0,57(BC +2) = BC y despejando
BC = 2,65 m
19. Epi y Blas ven pasar un avión con ángulos respectivos de 30º y 45ª. Si la distancia que les separa es de 2km, calcula la altura a que vuela el avión en todos los casos posibles.
20. Calcula la altura de un semáforo, sabiendo que desde un cierto punto A, se ve bajo un ángulo de 60º y si nos alejamos 40 metros se ve bajo un ángulo de 30º.
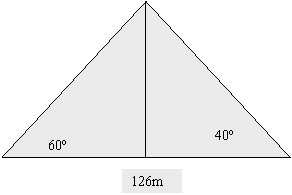21. Una
antena de radio está sujeta al suelo con dos cables de acero tirantes, como se
indica en la figura. Calcula:
a) La altura de la torre.
b) La longitud de los cables.
22. La distancia de un barco a un faro es de 137 m , y a la orilla 211m. El ángulo bajo el cual se ve desde el barco el segmento cuyos extremos son el faro y la orilla es de 43º. ¿Qué distancia hay entre el faro y la orilla?
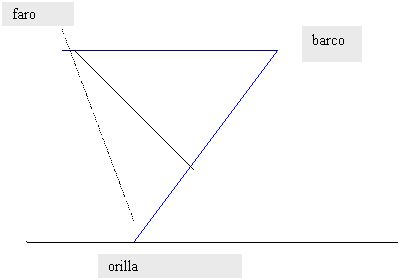137
m
sen 43º =h/137 43º
h = 137.sen 43º=93,43 m h
x
cos 43º = x/137 y 211 m
x = 137.cos 43º =100,20
211-100,20=110,80m
Aplicando el T. Pitágoras
y2= 93,432 +110,802 = 21005,18
y = 144,93m
23. Dos barcos salen de un puerto con rumbos distintos formando un ángulo de 54º, y con velocidades de 21 y 24 millas/h, respectivamente. ¿A qué distancia se encontrarán al cabo de una hora?
INICIACIÓN A LA GEOMETRÍA ANALÍTICA PLANA
Cuaderno de actividades 4º ESO
