INICIACIÓN A LA GEOMETRÍA ANALÍTICA PLANA

 

SISTEMAS DE REFERENCIA CARTESIANO

En el plano consideramos el sistema de referencia cartesiano, dos rectas perpendiculares que se cortan en el punto O(0, 0). OX es el  eje de abscisas, OY es el eje de ordenadas.

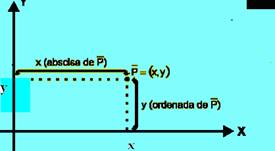
Con este sistema cada punto del plano, P, se puede representar por dos números que llamamos  coordenadas y representamos entre paréntesis, P(x, y)  (ver dibujo).  La primera “coordenada”, x,   se llama abscisa,  la segunda coordenada, y, se llama ordenada.

SIGNO DE  LAS COORDENADAS DE LOS PUNTOS EN LOS CUATRO CUADRANTES

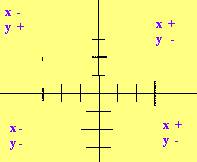
En el primer cuadrante las dos coordenadas son positivas, en el segundo la abscisa es negativa y la ordenada positiva, en el tercero las dos son negativas y en el cuarto la abscisa es positiva y la ordenada negativa.

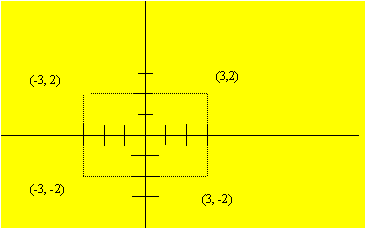
Ejemplo 1. Dibuja los puntos de coordenadas A( 3, 2), B(-3, 2), C(3, -2) y D(-3, -2)

DISTANCIAS ENTRE DOS PUNTOS

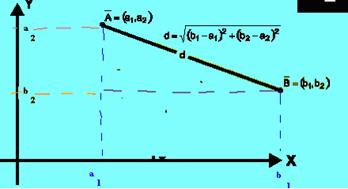
Si tenemos dos puntos A(a₁, a₂) y B(b₁, b₂) la distancia entre esos dos puntos es:

d(A, B)=, lo cual se puede demostrar aplicando el Teorema de Pitágoras (ver figura)

Ejemplo 2. La distancia entre los puntos A(2, -1) y B( 3, 3) es

SEGMENTOS. PUNTO MEDIO DE UN SEGMENTO

Si consideramos el segmento AB, , la longitud del segmento es la distancia de A a B, es decir :

Longitud =

El punto medio de un segmento dado por sus coordenadas se puede comprobar que es de la forma

P_M =

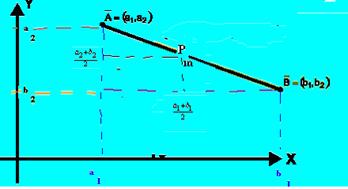
Ejemplo 3. El punto medio del segmento , donde A(2, -1) y B( 3, 3) es

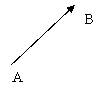VECTORES EN EL PLANO

Dados los puntos del plano A(a₁, a₂) y B(b₁, b₂)  llamamos vector fijo de origen A y extremo B, al segmento orientado :

 

 

La coordenadas del vector  se obtienen restando a las coordenadas del punto extremo las del origen. Es decir las coordenadas de  son (b₁ -a₁, b₂-a₂)

Ejemplo 4. Las coordenadas del vector , donde A(2, -1) y B( 3, 3) son (3 -2, 3+1)=(1, 4)

Se llama módulo del vector a la longitud del segmento . Dirección del segmento la de la línea que la contiene o de cualquier paralela. Sentido el que indica la flecha.

Ejemplo 5. El módulo del vector del ejemplo 4 es

VECTORES EQUIVALENTES

Dos vectores son equivalentes (a este nivel los consideramos iguales) si tienen el mismo módulo, dirección y sentido. Se suelen representar , , ..., o con negrita, u, v...

Se dice que un vector fijo tiene la misma dirección que otro si los segmentos que los definen pertenecen a rectas paralelas.

Ejemplo 6. Los vectores y , donde A, B, D y C son los vértices de un rectángulo, son equivalentes,

Se verifica que dos vectores equivalentes tienen las mismas coordenadas.

Dos vectores con igual módulo, dirección pero con distinto sentido son “opuestos”. Sus coordenadas son las opuestas.

Ejemplo 7 los vectores (3, 2) y (-3, -2) son opuestos.

PUNTOS ALINEADOS

Tres puntos A, B y C están alineados si los vectores y  tienen la misma dirección y sus coordenadas son proporcionales.

 Suma de vectores

Sean  ,  dos vectores, su suma + es:

 

                           

 

 

( regla del paralelogramo)

 

( La resta  -  daría la otra diagonal, haz un dibujo apropiado para comprobarlo)

Si los vectores vienen dados por sus coordenadas, se suman sus coordenadas.

Ejemplo 8: Dados los vectores u(3, -1) y v(2, 4), la suma es u +v =(5, 3)

Comprobarlo gráficamente.

VECTOR DE POSICIÓN

Dado un punto A(a₁, a₂) el vector  se llama de posición del punto A.

 

 

 

 

 

 

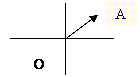ECUACIONES DE LA RECTA EN EL PLANO.

La “ecuación de la recta” expresa la condición que deben de cumplir sus puntos para pertenecer a ella.

Hay varias formas de determinar una recta.

POR UN PUNTO Y UNA DIRECCIÓN

- Una recta queda determinada por un punto A(a₁, a₂) y por un  vector de dirección )

                                                            Se verifica que  ecuación vectorial

                             X                           En coordenadas X(x₁, x₂)= (a₁, a₂)+ t(v₁, v₂) y:

          A                                              x₁ =a₁+ t v ₁

                                                           x₂ = a₂+ t v₂      ecuaciones paramétricas

                         

                                                           Ejemplo 9:  la ecuación vectorial de la recta que pasa por el punto (2, -1) y       tiene el vector de dirección (3, 4) es:

                       

                        O                                 (x, y) = (2, -1)+t(3,4)

Las ecuaciones paramétricas son:        

Ecuación continua

Si eliminamos el parámetro t, obtenemos:

                                   que se llama ecuación continua de la recta.

 

Ejemplo 10: la ecuación continua:       

Ecuación cartesiana o implícita

De la ecuación continua se tiene

v₂(x₁-a₁)=v₁(x₂-a₂)       

v₂x₁ –v₁x₂-v₂a₁ +v₁a₂=0, que se puede escribir A x + B y + C = 0

 

Ejemplo 11:  La ecuación cartesiana: 4(x-2)=3(y +1)

4x-8= 3y+3. de donde 4x – 3y -11=0

Si se despeja la y  se llega a la ecuación explícita de la recta:

y = mx +n

La m se llama pendiente o coeficiente angular. La n la ordenada en el origen.

Se puede comprobar que m =v₂/v₁

RECTA DETERMINADA POR DOS PUNTOS

Dos puntos del plano A(a₁, a₂) y B(b₁, b₂)   determinan una recta. Lo podemos reducir al caso anterior, en primer lugar se debe encontrar lo que hemos llamado vector de dirección. Lo conseguimos sin más que considerar el vector de origen A y extremo B, es decir v =, entonces la ecuación continua  de la recta que pasa por dos puntos es:

La pendiente es  m =

 

 

Ejemplo 12. Ecuación continua de la recta r que pasa por los puntos A(-1, 3) y B(2, 2).

El vector v tiene de coordenadas (3, -1), la ecuación de la recta que pasa por A y tiene como vector de dirección v es:  

                                     la pendiente es -1/3

Observación. La ecuación explícita de la recta y = mx +n se puede calcular planteando un sistema  

Ejemplo 13. Hallar la ecuación explícita de la recta r que pasa por los puntos A(-1, 3) y B(2, 2) y calcular su pendiente.

Se tienen que calcular m y n , y esto lo conseguimos imponiendo que la recta pase por los puntos A y B.

Por pasar por A(-1, 3)  se tiene 3 = -m +n

Por pasar por B(2, 2)  se tiene   2= 2m + n

Resolvemos el sistema por reducción:    1= -3m ,          

m = -1/3 y sustituyendo n =3+ m =3-1/3=8/3

La recta es

POSICIÓN RELATIVA DE RECTAS

Si dos rectas tienen la misma dirección se dice que son paralelas. Cuando no son paralelas se cortarán en un punto, se dicen secantes. Dos rectas pueden ser secantes o paralelas.

Si son paralelas tienen la misma pendiente.

Se puede determinar una recta conociendo uno de sus puntos y una paralela a ella. Hay varias formas de determinar este tipo de rectas, depende el método de cómo te den la paralela.

Ejemplo 14. Calcula la recta que pasa por el punto A(0, 3) y es paralela a la recta 2x-3y-4= 0.

En este caso consideramos el haz de rectas paralelas a 2x-3y-4=0  que es 2x-3y+ c = 0, donde c es una constante. Determinando c obtendremos la recta del haz que pasa por A.

Como pasa por A, este punto tiene que verificar la ecuación:  2.0-3.3+ c =0, c =9, y la recta 2x-3y+9=0

Ejercicios propuestos

1. a)Encuentra la ecuación de la recta r que pasa por los puntos A(-1, 2) y B(2, 3) en todas las formas que conozcas.

b) Halla la pendiente de r.

c) Encuentra la  paralela a la recta 2x +y =1 y que pase por A.

2. Dados los puntos del plano P(1, 2) y Q(-3, 1), se pide:

a) Encontrar de forma razonada la ecuación de la recta que pasa por ambos puntos,

b) deducir si dicha recta es paralela o si corta a la recta de ecuación x +4y =5 y,

c) en este último caso, calcular el punto de corte.

3. Dados los puntos A(2, -3), B(0, 1) y C(4, 0) hallar:

a) ecuación de la recta r que pasa por A y B en todas las formas que conozcas.

b) ecuación implícita de la recta s que pasa por B y C.

c) intersección de r y s.

d) ecuación de la recta paralela a r que pase por C.

 

PARA COMPLETAR EL TEMA VISITA: ACTIVIDADES