Teorema de Pitágoras
En un triángulo rectángulo se verifica que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos.
Demostración
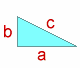 |
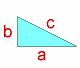
Consideremos el triángulo de la figura , a y b son los catetos y c la hipotenusas. Tenemos que probar que c2= b2+ a2
|
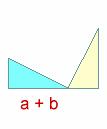
Vamos a construir un cuadrado de lado la suma de los catetos, a +b, el proceso se indica gráficamente.
El
triángulo del que partimos tiene por área
El cuadrado exterior así construido tiene por lado la suma de los catetos, es decir a +b , y por tanto su área es (a +b)2
Ahora
bien, el cuadrado así construido, está formado por cuatro triángulos de área Por lo tanto se verifica:
(a +b)2= 4.
y teniendo en cuenta la identidad notable:
(a +b)2= a2 + b2 + 2ab se deduce que
c2 = a2 + b2 que es lo que pretendíamos probar
|
(los triángulos son iguales) |
|
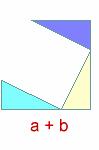
Y por fin con el triángulo rojo (igual que los otros), conseguimos un cuadrado de lado a +b
|
|
|
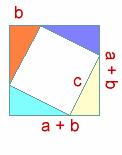
Observar por la construcción que esta
formado por 4 mas un
cuadrado de lado la hipotenusa c |