ESTA PÁGINA ESTÁ PENSADA PARA LA ESO,  SI NECESITAS FUNCIONES Y GRÁFICAS DE BACHILLERATO VISITA:  MATEMÁTICAS EN EL BACHILLERATO     Ó        CUADERNO 2º BACH

4ª Parte: Funciones y sus gráficas

Relaciones funcionales.

Estudio gráfico y algebraico de funciones.

Interpretación de gráficas

 

 1. Un médico dispone de 1hora diaria para consulta. El tiempo que podría, por término medio, dedicar a cada enfermo, depende del número de ellos que se acudan:

1 enfermo                                                  60 minutos

2 enfermos                                                30 minutos

3 enfermos                                                 20 minutos

.....  .......   ......... ......

Así hasta un máximo de 30 enfermos. Si llamamos x al número de enfermos e y al de minutos dedicados a cada enfermo escribe la expresión funcional que existe entre ellas ¿ Cómo es la variable independiente, continua o discreta? Dibuja la gráfica ¿ Tiene sentido unir los puntos de la gráfica con una línea?

 

2. En unos aparcamientos públicos figura la siguiente tarifa de precios:

                               Tarifa

1ª hora o fracción                                                                     1 €

Cada hora más o fracción                                                       0,8 €

Máximo 12 € por 24 horas

Haz una gráfica representativa de la función : tiempo de aparcamiento ....... coste

 

3. Si un coche va a 80km por hora, ¿ que espacio habrá recorrido al cabo de 2, 3, y 3,5 horas?

a) Dibuja la gráfica de la función espacio-tiempo.

b) ¿Qué tiempo empleará en recorrer 200km?,  y¿ 320km?                                          

Solución

                La función es e =v. t = 80.t  , al cabo de 2 horas ha recorrido 160km, al cabo de 3 horas,240km, al cabo de 3,5 horas , 280km-

a) es una recta

                              

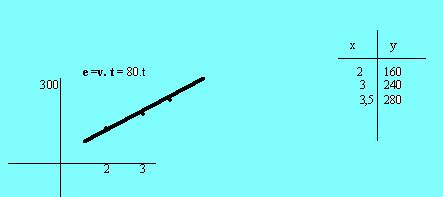
b) Despejando el tiempo tendremos t =e/v:

t = 200/80 = 5/2 = 2horas y media  y t = 320/80 =4 horas

4. Representa los siguientes pares (x, y) . Indica la relación entre las variables x e y:

 

x

1

3

4

5,5

7

....

y

0,75

2,25

3

4,125

5,525

....

5.  Dada la tabla

x

0

1

2

3

4

....

y

1

3

5

7

9

....

Representa estos puntos en un sistema de ejes coordenados y escribe la ecuación de la función que relaciona las variables x e y.

 

6. Halla el dominio de las siguientes funciones:

a) y = 3x                                                                                               b) y = x2-3

 

c) y =             D =R +                                                                   d) y =  1/x              D = R -{0}

 

e)                                                                                        f)

 

7.  Estudia la continuidad de las siguientes funciones:

a)

 

 

 

                                                                                              Continua excepto en el x =0.

 

 

 

 

 

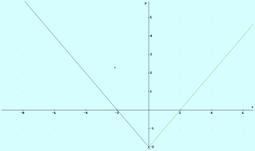
b)

 

                                                                                              Continua en todos los puntos.

 

 

 

 

 

8. Estudia la continuidad de las siguientes funciones:

a)

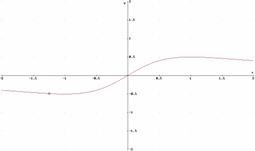
b)


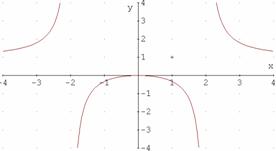
9.  Para las funciones del ejercicio anterior. Estudia la monotonía, simetría y los máximos y mínimos.

 

b) creciente en ]-4, -2[ È]-2, 0[ y decreciente en ]0, 2[È]2, 4 [

simétrica respecto el eje OY

mínimo no tiene, el máximo relativo se alcanza en el 0 y vale 0

 

10.  Estudia la monotonía, simetría y los máximos y mínimos de la función cuya gráfica es la de la figura.


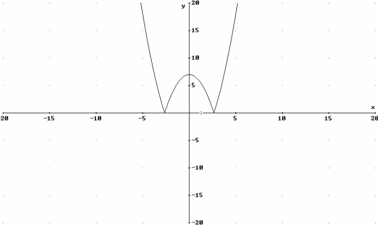11. Antonio ha comprado un coche que le ha costado 19500 €. El coche se deprecia un 20% cada año. Al cabo de un tiempo decide venderlo y le dan 5200 € . ¿Cuántos años han pasado?

Indicación: Haz la gráfica de la situación planteada y encuentra el punto de la gráfica cuya ordenada valga 5200.

12. Dibuja en el intervalo [0, 6] la función que a cada número positivo le hace corresponder su parte entera.

13. Halla la pendiente de las rectas que pasan por los puntos:

a) (2. 3) y (-1, 0)

b) (3, 1) y (4, -5) . Solución

14. Halla la pendiente de las rectas:

a) y = -3x +1

b) y = 2-x

c) 3x-2y-4=0

d)  

15. Representa las siguientes funciones lineales o afines:

a) y =2x  ; b) y =3; c) y = 3x-2; d); e)

16. Halla gráficamente la pendiente de la recta que pasa por los puntos A(-3, -6) y B((3, -2) y escribe su  ecuación.

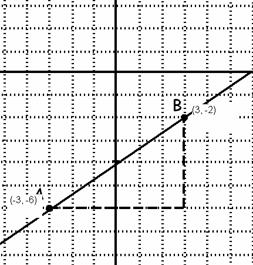Solución

La pendiente según se ve en la gráfica es

 

 

la ordenada en el origen es -4

y por tanto la ecuación es

                              

 

 

 

 

 

 

 

17. Dibuja y halla la ecuación de la recta que pasa por los puntos:

a)  (2. 3) y (-1, 0)

b) (3, 1) y (4, -5)

 

18. Hallar la ecuación de cada una de las siguientes rectas:

a) Pasa por el punto (0, 1) y tiene por pendiente 3

b) Pasa por el punto (0, 4) y tiene por pendiente 3/4

c) Pasa por el punto (-3, 3) y tiene por pendiente -4

 

19. Calcula la expresión de la función cuya gráfica se adjunta:

Solución

 

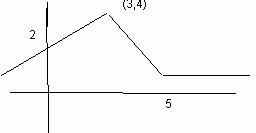                                                                                              Es una función definida a trozos.

                                                                                              El primer trozo pertenece a la recta que pasa por los

                                                                                              Puntos (0,2) y (3,4), Su ecuación es

                                                                                                              y = 2x +2

                                                                                              El otro trozo pertenece a la recta que pasa por (3, 4)                                                                                                  y  (5, 1).

                                                                                               La pendiente es:  

                                                                                                              y =

El último trozo pertenece a la recta constante y =1

 

La función es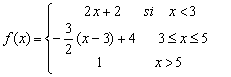

                                                                                                                                            

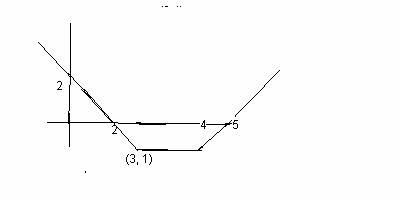
20.  Calcula la expresión algebraica de la función cuya gráfica es:

21. Representa en los mismos  ejes coordenados las siguientes rectas:

a) y = x    e   y = 2 – x

Solución

 

 

 

 


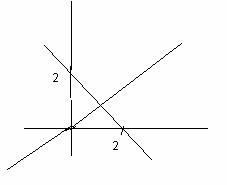                Las rectas se cortan en el punto (1, 1)

 

 

 

 

 

 

 

 

 

 

b) y = x-3   e    y = -x +2;

c)  e 

22. En la factura del gas de una ciudad se paga una cantidad fija de 120 € y 0,40 € por cada m3. Calcula:

a) ¿Cuánto hay que pagar por cada m3? ¿Y por 15 m3?

b) Representa la función que nos dice lo que tenemos que pagar según los m3 consumidos?

 

23. Un ciclista sale de un lugar, a las 9 de la mañana ,a una velocidad de 20km/h. A los 30 minutos un amigo suyo sale a su encuentro a 25km/h. Se pide:

a) Dibuja en unos ejes coordenados las gráficas que representan estas situaciones

b) ¿A qué hora le alcanza? ¿que espacio ha recorrido?

 

 

 

 


                   Para profundizar                                                                                                Cuaderno actividades 3º

 

 

Si observas algún error o errata en la página  te agradecería lo comunicaras a través del correo   o del foro (situado en la página principal) , para poder corregirlo en la próxima actualización.