Si quieres teoría de ecuaciones la puedes encontrar en el cuaderno de actividades de 4º (en Ecuaciones )
Ecuaciones de 1er grado
Resuelve las ecuaciones siguientes:
1) 
Para resolver la ecuación seguiremos el siguiente orden.
1º Quitar denominadores
Al multiplicar los dos miembros de una ecuación por el mínimo común múltiplo de sus denominadores, se obtiene otra ecuación equivalente a la primera, pero sin denominadores.
Multiplicamos los dos miembros de la igualdad por 6, que es el m.c.m. de los denominadores.
Nos queda 3(2x-3) -2(5x-1) =6
2º Quitar paréntesis
Se efectuarán las operaciones indicadas, utilizando la propiedad distributiva.
Quitando paréntesis 6x-9 –10x+2=6
3º Trasposición de términos
Se disponen todos los términos que llevan x en un miembro y los demás en el otro.
Trasponiendo términos 6x –10x = 9 - 2 + 6
4º Reducción de términos semejantes
De este modo cada miembro de la ecuación queda con un solo término:
-4x = 13
5º. Despejar la incógnita
Se
dividirá ambos miembros por el coeficiente de la incógnita (se puede hacer
siempre que sea a
0)
Observación. Dependiendo de la ecuación a resolver puede ocurrir que alguno de los pasos sea innecesario, se omite y se pasa al siguiente.
2)
3) 
4) 
5) 
8) 
Solución.
Multiplicamos los dos miembros por 8 (es el m .c. m. de los denominadores)
(2x-4)2 = 40 +4x(x +1)
4x2 –16x +16 = 40 + 4x2 +4x
4x2 –16x +16 =40 +4x2 +4x
Reduciendo términos semejantes:
16x-4x= 40- 16 -20x =24 
=
-1,2
7) 
8) 
Ecuaciones de segundo grado
Resuelve las siguiente ecuaciones indicando si son completas o no:
1) 3x2+ 2x=0
2) 5x2-3=0
3) x2-4x+2=0
4) 2x2+ x-1=0
5) 3 x2-
=0 Þ 3x2 = Þ x2=
Þ x =
6) –x2 + 4 =0
8) 4x2 –4x +1 =0
9) –x2 +6x-5=0
10) –6x2 +5x-1=0
11) (5x-4)(2x+3) =5
Sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales.
Ejemplo 16: 
es
un sistema de 2 ecuaciones con dos incógnitas
Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.
Hay tres métodos para resolverlos:
Sustitución
Ejemplo 17. 
En la 2ª ecuación despejamos la y y la sustituimos en 1ª ecuación
y =3x; 2x +3(3x) =1Þ 11x =1
Þ x =1/11
Una vez encontrado el valor de una de las incógnitas se sustituye (y =3x) para encontrar el valor de la otra incógnita: y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de, al menos, una de las incógnitas es 1.
Igualación
Ejemplo 18.
Despejamos la misma incógnita en las dos ecuaciones
;
y =3x.
Igualando 
Þ 1-2x =9x Þ 1=
11x Þ x =1/11
Ahora para obtener el valor de la y se procede como en el caso anterior, es decir se sustituye el valor hallado en la ecuación que más convenga ( en este caso en y =3x). y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de una de las incógnitas es igual en las dos ecuaciones.
Reducción
Ejemplo 19. 
Multiplicamos la 1ª ecuación por 2 y la 2ª por 3. (De esta forma el coeficiente de y en las dos ecuaciones es el mismo, el m.c.m.
Resulta: 
Þ 
Sumando obtenemos 13 x =2 Þ
Sustituyendo el valor encontrado de x en la segunda ecuación:
y
=3/13
Observación. Este método es muy adecuado en todos los casos.
Nota. A veces es más cómodo usar la reducción dos veces para encontrar el valor de la otra incógnita. (Ver ejercicio resuelto)
Ejercicios
Resuelve los siguientes sistemas por el método que creas más adecuado:
1) 
2) 
3) 
4)
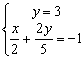
5) 
6) 
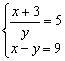
8) 
Problemas de aplicación
1) La suma de dos número es 65 y su diferencia 23. Halla los números
2) La diferencia de dos números es 1/6. El triple del mayor menos el doble del menor es 1. Halla dichos números.
Resolución de Problemas
1.. Alejandra tiene 27 años más que su hija Carmen. Dentro de 8 años, la edad de Alejandra doblará a la de Carmen. ¿Cuántos años tiene cada una?
Solución. Sólo en este problema indicaremos con detalle las 4 fases
1º. Comprender el problema.
Es un problema con dos incógnitas y dos condiciones, luego suficientes para poder determinarlas.
Llamamos x a la edad de Alejandra e y a la de su hija.
Ordenamos los elementos del problema:
|
|
Hoy |
dentro de 8 años |
|
La madre |
x |
x + 8 |
|
La hija |
y |
y + 8 |
2º. Concebir un plan.
Escribimos las ecuaciones que relacionan los datos con las incógnitas:
x = 27 + y
x + 8 = 2(y +8)
Es un sistema lineal de dos ecuaciones con dos incógnitas. Lo resolveremos por el método de sustitución.
3º Ejecutar el plan.
X = 27 + y
Entonces:
27 + y +8 = 2(y +8) de donde 35 -16 = y Þ y = 19, x = 46
4º Examinar la solución obtenida .
La solución obtenida es factible por ser entera.
El método empleado se puede usar en problemas “similares”.
2. La edad de una madre es siete veces la de su hija. La diferencia entre sus edades es de 24 años. ¿qué edad tienen?.
Solución
Llamamos x a la edad de la hija, luego 7x será la edad de la madre.
7x –x =24Þ 6x =24 Þ x =4
Luego edad de la hija 4 años y edad de la madre 28 años
3. El hermano mayor de una familia con tres hermanos tiene 4 años más que el segundo y éste 3 más que el menor. Si entre todos tienen la edad del padre que tiene 40 años ¿qué edad tiene cada hermano ?
4. Halla un número tal que su mitad más su cuarta parte más 1, sea igual al número pedido.
Solución
Llamamos x al número que buscamos, la mitad del número es x/2 y su cuarta parte x/4
Entonces: 
Multiplicamos por el m.c.m. que es 4. Nos queda:
2x +x + 4 = 4x
x =4
5. El perímetro de un jardín rectangular es de 68 m. Si el lado mayor mide 10 m. más que el lado menor. ¿Cuánto miden los lados del jardín?
6. Un gavilán se cruza en vuelo con lo que parece un centenar de palomas. Pero una de ellas lo saca de su error:
- No somos cien -le dice-. Si sumamos las que somos, más tantas como las que somos, más la mitad de las que somos, y la mitad de la mitad de las que somos, en es caso, contigo, gavilán, seríamos cien.
¿Cuántas palomas había en la bandada?
7. Un ciclista sale por una carretera a 15km / h. Media hora después sale otro en su persecución a una velocidad de 20km/h. ¿Cuánto tardarán en alcanzarse
8. Halla un número tal que su mitad más su cuarta parte más 1, sea igual al número pedido.
