En esta página se recogen actividades, ejercicios y problemas, resueltos y propuestos, para 1º de Matemáticas Aplicadas a Las Ciencias Sociales y enlaces al Cuaderno de 1º, así como a otros recursos de la Web a que pertenece
Observaciones:
-En esta primera parte de álgebra se repasan y amplían: las operaciones con números reales, la recta real, intervalos. Los polinomios, regla de Ruffini, Teorema del resto, ... Las fracciones algebraicas hasta la descomposición en fracciones simples
-La parte de ecuaciones, sistemas (de todos los tipos) e inecuaciones está en el siguiente enlace: Ecuaciones y sistemas
-El cuaderno de 1º está pensado, sobre todo, para las Matemáticas Aplicadas a la Ciencias Sociales y por eso se incluyen además bastantes ejercicios de repaso de la ESO. Dependerá del nivel del curso el hacerlos todos o no.
-Si buscabas álgebra para el 2º de bachillerato te recomiendo que visites Álgebra 2º (LOGSE) o Álgebra en el bachilleratol
S tienes alguna duda o sugerencia visita el FORO y déjanos tu mensaje
ÁLGEBRA 1º
Operaciones con reales
1. Representa en la recta real los números racionales
-3/4; 5/3; 7/2; 2,45
2. Calcula pasando a fracción:
a)
b)
c)
3. Calcula, sin usar la calculadora, las siguientes raíces exactas:
a)
; b)
;
c)
d)
e)
f) 
g)
h)
f) Solución. 
=
4. Calcula por tanteo, sin usar la calculadora, una aproximación decimal de los siguientes números irracionales:
a)
b) 
;
Solución: 62=36; 72=49, luego está entre 6 y 7 6,82=46,24
6,92=47,61 Con un decimal la aproximación seria 6,8
6,842=46,78;
6,852=46,92; ,6,862=47,05. Luego 
=6,85 con dos
decimales exactos
c) 
d)
5) Escribe tres aproximaciones decimales de los números irracionales
a)
b)
6) Calcula la cota del error que se comete al
sustituir el número por:
a) 3,14
b) 3,142
Solución. Tiene tres cifras decimales exactas, luego el error que se comete es menor que 10-3
c) 3,1415
7) Escribe las
aproximaciones por defecto del número 
, con
las mínimas cifras para que el error cometido sea menor que:
a) una décima.
b) una milésima
8) Calcular la altura de un triángulo equilátero cuyo lado mide20cm, con un error menor que una milésima.
9. Simplifica:
a) 
b 
c) 
Solución. Primero
reducimos las potencias a bases positivas 
=+=782-75-2
d) 
10. Escribe con notación científica::
a) 310000000000
b) 0,00000023=2,3.10-7
c) 1540,23
d) El número de moléculas que hay en un gramo de hidrógeno: 301000000000000000000000
e) La longitud de un paramecio: 0,000025 m
11. Realiza las siguientes operaciones:
a) 2,43.10-23.1,35.1021
b) (3,21.107): (2,51.10-4)
c) 
Solución. =
=9,79.1013
d)
12. Opera los siguientes radicales y/o simplifica cuando sea posible:
a)
b)
c) 
d)
c) Solución.
Se reducen a índice común y después se multiplican los radicandos.
m. c. m (2,3)=6 =
=
e)
f)
g) 
h)
i) 
Solución
180=2232.5 
80=24.5 
=3
5
j)
k)
13) Racionaliza:
a) 
=
|
b) |
|
c) |
14) Representa en la recta real los números reales:
Solución. Utilizamos el Teorema de Pitágoras. 5 = 12+22
Se dibuja un triángulo de catetos 2 (base) y 1(altura)
es la
diagonal del triángulo, con un compás de origen 0 se obtiene donde está
situado.
La recta real. Intervalos.
1) Escribe en forma de desigualdad y representa los siguientes intervalos:
a) [-3, 2]
b) (1, 3)
c) [-1, 0)
Solución. [-1, 0)=
-1é
ö0
2) Expresa como una desigualdad y como un intervalo: “ x es un número mayor o igual que -5 y menor que 2”. Represéntalo.
3) Escribe en forma de intervalo y representa los conjuntos:
a) 
b) 
c) 
4) Representa el conjunto de los números que cumplen:
a) 
b) 
c) 
d) 
-2
[2,
6]
e) 
f) 
<3
g) 
5) Expresa como un único intervalo
a) [3, 5)È(2, 7]
b) (-1, 4)È [3, 5)
c) [-1, 3) È[3, 5]
Polinomios
Efectúa las operaciones indicadas y simplifica la expresión resultante (en los casos posibles).
1) 3(x3 –5x +7) –(2x3 +6x2 +11x+4)
2) 2x(4x2 –6x +2) +3 (5x2 –3x-4)- 14 x2
3) (7x3 –5x+3) (2x2 +x-1)
4)
5) Multiplica por 20 y simplifica el resultado:
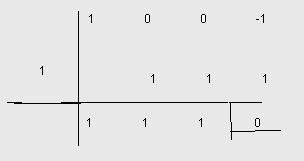
6) (x3 +6x2 +5x+4): (x2 –3x +1)
Solución
x3
+ 6x2 +5x +4 x2 –3x +1
-x3 +3x2 -x x +9
/ 9x2 + 4x +4
-9x2 + 27x-9
/ 31x –5
7) (x3 +6x2 +5x+4): (x2 –x +5)
9) (x4 -5x3 +3x2-2x+5): (x2 +x -3)
Regla de Ruffini
Se usa para divisiones en que el divisor es de la forma (x-a)
Se ordena el polinomio en potencias decrecientes y se cogen sólo los coeficientes, si falta alguna potencia de x, su coeficiente es cero, en su lugar se pone un cero.
(Ver ejemplo 6 y en ejercicio de raíces el 3.a))
6) (x3 –x2 -16x -3): (x -3)
el cociente es x2 +2x – 10 y el resto -33
7) (2x3 +6x2 +11x+4):(x +1)
8) (3x4 +6x2 +11x+4) : (x-2)
9) (x3 + 1) : (x +1)
10)( –x4 +2x3 +5x -3): (x +2)
Raíces de polinomios. Teorema del resto
El valor numérico de un polinomio en x = a es el que se obtiene al sustituir la indeterminada por a.
Las raíces o ceros de un polinomio son los valores que lo anulan.
1. Comprueba si los valores que se dan son raíces de los siguientes polinomios:
a) x2 +1 0, -1
Solución. Para 0 el valor numérico del polinomio es 1, luego no es raíz
Para -1 “ “ 2 “
b) x2 -5x +6 0, 2 y 3
c) x2 -4 2 y .-2
d) x3 -1 -1, 0, 1 y 2
3. Calcula las raíces de los siguientes polinomios.
a) (x3 -1): (x-1)
Aplicamos Ruffini
El cociente es x2 + x + 1, el resto 0.
La única raíz es x = 1, pues el cociente no tiene ninguna raíz más.
b) x3 -11x2 +34x -24
c) x4 -11x3 +33x2 -9x -54
d) x4 -81
e) x4 +x2 -20
f) 2x3 -8x2 +8x
Teorema del resto ( o teorema del residuo)
El resto de la división de un polinomio P(x) entre el binomio (x-a) es el valor numérico del polinomio en x =a, es decir el resto es el valor de P al sustituir la x por a, R =P(a).
Demostración:
Por el algoritmo de la división entera: Dividendo = Divisor x Cociente + Resto,
Se verifica P(x) = (x-a)C(x) + R, si sustituimos la x por a, nos queda,
P(a) =(a-a)C(x)+R = 0 +R, es decir, P(a) = R
Aplicación: Sirve para calcular el resto sin efectuar la división
4. Calcula el valor de k para que la división de P(x) entre Q(x) dé exacta:
a) P(x) = ) x3 -11x2 +k.x -24, Q(x) = (x-1)
Si la división es exacta, el resto debe dar cero, aplicando el teorema del resto: resto =P(1)=0
Sustituyendo el valor de x por 1, se tiene:
P(1)=1 -11 + k -24 = 0, de donde k = 34
b) P(x) = x4 -11x3 +33x2 –k x -54; Q(x) = (x +1)
5. Calcula el valor de k, para que el resto de la división de x4 –k x3 +33x2 –k x -54 entre x +2 nos de 25.
Factorización de polinomios
Factorizar un polinomio es ponerle como producto de sus factores (se llama también descomposición en factores del polinomio).
Por ejemplo, si el polinomio solo tiene raíces reales y simples (r1, r2, ....rn, quedará de la forma:
P(x)= A(x-r1)(x-r2)....(x-rn)
Para factorizar hay que tener en cuenta las identidades notables, el sacar factor común, la regla de Ruffini, y la resolución de ecuaciones (de 2º grado) para la búsqueda de raíces.
6.1 Descomponer en factores:
a) x2 -2x +1
b) x3-5x2+ 4x
Solución
En primer lugar se saca factor común x, x3-5x2+ 4x =x(x2-5x+4)
El segundo factor es un polinomio de 2º grado, y para encontrar los otros factores se puede obtener las raíces aplicando la fórmula de la ecuación de 2º grado.
x
=
por tanto
los factores son (x-4) y (x-1)
El polinomio factorizado es: x(x-4)(x-1).
Nota: También podría haberse usado Ruffini para el cálculo de las raíces, ya que son enteras
d) x3 -11x2 +34x -24
e) x4 -11x3 +33x2 -9x -54
6. 2. Descomponer en factores los polinomios P(x) y Q(x) y hallar su M .C .D y M . C . M
a) P(x) = x3 -1 y Q(x) = x2 -2x +1
Solución
P(x) = (x – 1) (x2 + x + 1)
Q(x) = (x -1)2
M. C. D. = x-1 M. C. M. = (x-1)2(x2 + x + 1)= x4 –x3-x+1
b) P(x) =3x3+ x2-8x+4 y Q(x) =3x3 +7x2-4
c) P(x) = x7 –x y Q(x) = x5 +x2
Fracciones Algebraicas
A) Hallar el valor numérico de las siguientes fracciones algebraicas en los puntos que se indican:
1)
en
x = 1, x =3.
2)
en
x = 2, x = 0.
3) 
en x
=1, x =2
Solución:
En x
= 1 
No existe este valor, pues no se
puede dividir por cero, luego no se puede calcular el valor numérico en x =1.
En x
=2 
4)
en x = -2, 0,
1 y 2
B) Estudia si las siguientes fracciones son equivalentes:
1)
y
2) 
y
Solución. Se tiene:
(x-2)(x2-4) = x3 -4x -2x2+8 = x3 -2x2 -4x +8
(x +2)(x2-4x+4) = x3 -4x2 +4x+ 2x2 -8x +8 = x3 -2x2 -4x +8
Son equivalentes.
C) Simplifica las siguientes fracciones algebraicas, en los casos posibles:
1) 
2) 
3) 
4)
5)
Solución.
Se tiene ==
6) 
D) Realiza las operaciones indicadas y simplifica el resultado en los casos que se pueda.
1)
.
2)
3) 
Solución. Primero reducimos a común denominador y después sumamos los numeradores:
m .c. m (x, x +1) = x(x +1) =x2+ x
=
4)
5) 
6) 
7)
D) Descomposición en fracciones simples:
Esta basado en el siguiente teorema:
Si x1, x2,......, xn son las raíces simples de Q(x) se verifica*:
donde A1, A2,....., An son números reales que hay que determinar
(*El grado de P tiene que ser menor que el grado de Q)
Veamos como se encuentran éstos coeficientes con un ejemplo:
Descomponer en fracciones 
Igualando a cero el denominador:
Las raíces son 0 y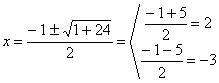 
Luego descomponiendo la fracción en fracciones simples, se tiene:
y se trata de calcular estas constantes.
Se tiene, efectuando la suma e igualando los numeradores,
x +1= A1(x-2)(x +3)+A2x (x +3)+ A3x(x-2)
Teniendo en cuenta que los dos polinomios son iguales, tomarán los mismos valores en todos los puntos, en particular:
Para x =0 0 +1= A1(-2)(3)
A1=-1/6
Para x =2 2+1= A2.2.5
A2
=3/10
Para x =-3 -3+ 1= A3(-3)(-5)
A3=-2/15
Ejercicios: Descomponer en fracciones simples
1) 
Solución
Se calculan las raíces del denominador (Comprobar que dan 2 y 3)
Entonces se verifica
y se
trata de encontrar A y B para que esto sea cierto
=
Como los denominadores son iguales, para que sean iguales las fracciones deben serlo también los numeradores:
Por lo tanto : 3= A(x-3)+B(x-2) y esto es cierto independientemente del valor de x.
Si x =2 entonces 3 =A(2-3)+B(2-2) de donde A = -3
Si x =3 nos quedaría 3= A(3-3)+B(3-2) de donde B = 3
Y la
descomposición pedida es 
Nota. También se podía usar el método de los coeficientes indeterminados, que es el que se usa de forma general pues vale también para el caso de raíces dobles o complejas
Para este ejercicio quedaría:
De 3=
A(x-3)+B(x-2) 
2) 
3) 
4) 
LA PARTE DE ÁLGEBRA DE 1º CONTINÚA EN EL SIGUIENTE ENLACE (PINCHA AQUÍ)
CUADERNO DE ACTIVIDADES 1º BACHILLERATO
Otras páginas:
