Ecuaciones y Sistemas[C1]
Resolver una ecuación es encontrar todas su soluciones o llegar a la conclusión de que no tiene ninguna.
Ejemplo 1. a) x2-1=0 tiene dos soluciones, x =1 y x =-1
b) x2 + 1=0 es una ecuación sin soluciones en R.
c) 2x +3y = 0 tiene infinitas soluciones, (0,0), (-3,2), (3, -2)....
Ecuaciones equivalentes
Dos ecuaciones son equivalentes cuando admiten la mismas soluciones. Se cumple:
v Si se suma o resta un mismo número a los dos miembros de una ecuación, se obtiene una ecuación equivalente a la primera.
v Si se multiplican o dividen los dos miembros de una ecuación por un mismo número distinto de cero se obtiene una ecuación equivalente a la primera.
Trasposición de términos. Aplicando las reglas anteriores deducimos dos reglas prácticas:
Ø Si un número aparece en un miembro sumando, se le puede pasar al otro miembro restando. Si esta restando pasará sumando.
Ø De igual manera si está multiplicando pasa dividiendo y al revés.
Esto se llama trasponer términos.
Ejemplo 2: La ecuación 5x - 1 = 2x -3 se puede escribir 3x + 2 = 0, trasponiendo términos.
Nota : El segundo miembro de la ecuación se puede considerar siempre que es 0.
Ecuaciones de primer grado
La
forma general de esta ecuación es a x +b =0
con a![]() 0
0
Trasponiendo
y dividiendo por a se llega a ![]() .
.
Solución que siempre existe y es única.
Ejemplo 3. a) 3x +2 =0 Þ ![]()
b) 7x + 2 = 2x -3 , si trasponemos términos, nos queda 7x –2x = -2 –3
Luego 5x = -5 de donde x = -1
Ecuaciones de segundo grado
La forma general
de una ecuación de 2º grado es: ![]() , donde a
, donde a![]()
La solución de esta ecuación general viene dada por la fórmula:
![]()
Ejemplo 8. ![]()
![]() =
=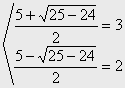
Observación. A D =![]() se llama discriminante de la
ecuación de 2º y se verifica:
se llama discriminante de la
ecuación de 2º y se verifica:
Si D>0 la ecuación tiene dos soluciones conjugadas
Si D =0 la ecuación tiene una única solución (doble)
Si D <0 la ecuación no tiene ninguna solución real.
Ecuaciones incompletas
- Si c =0 la ecuación se reduce a
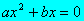 y sacando factor
común x se tiene:
y sacando factor
común x se tiene:
x(ax +b) =0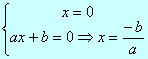
Este tipo de ecuación siempre tiene dos soluciones.
Ejemplo 4. 3x2-5x=0 x(3x-5)=0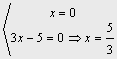
- Si
b =0 la ecuación queda
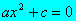 de donde
de donde
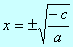
Puede tener dos soluciones opuestas o ninguna solución, dependiendo de que el radicando sea o no positivo.
Ejemplo 5. 2 x2-![]() =0; 2 x2=
=0; 2 x2=![]() Þ
Þ ![]() (dos soluciones)
(dos soluciones)
Ejemplo 6. 3x2+1 =0 ![]() (no tiene ninguna solución)
(no tiene ninguna solución)
Resolución “práctica” de una ecuación
Lo estudiamos con un ejemplo
Ejemplo 7. ![]()
Para resolver la ecuación seguiremos el siguiente orden.
1º Quitar denominadores
Al multiplicar los dos miembros de una ecuación por el mínimo común múltiplo de sus denominadores, se obtiene otra ecuación equivalente a la primera, pero sin denominadores.
Multiplicamos los dos miembros de la igualdad por 6, que es el m.c.m. de los denominadores.
Nos queda 3(2x-3) -2(5x-1) =6
2º Quitar paréntesis
Se efectuarán las operaciones indicadas, utilizando la propiedad distributiva.
Quitando paréntesis 6x-9 –10x+2=6
3º Trasposición de términos
Se disponen todos los términos que llevan x en un miembro y los demás en el otro.
Trasponiendo términos 6x –10x = 9 - 2 + 6
4º Reducción de términos semejantes
De este modo cada miembro de la ecuación queda con un solo término:
-4x = 13
5º. Despejar la incógnita
Se
dividirá ambos miembros por el coeficiente de la incógnita (se puede hacer
siempre que sea a![]() 0)
0)
![]()
Observación. Dependiendo de la ecuación a resolver puede ocurrir que alguno de los pasos sea innecesario, se omite y se pasa al siguiente.
Ecuaciones de primer grado
Resuelve
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Solución.
Multiplicamos los dos miembros por 8 (es el m .c. m. de los denominadores)
(2x-4)2 = 40 +4x(x +1)
4x2 –16x +16 = 40 + 4x2 +4x
4x2 –16x +16 =40 +4x2 +4x
Reduciendo términos semejantes:
16x-4x=
40- 16 -20x =24 ![]() = -1,2
= -1,2
6) ![]()
Ecuaciones de segundo grado
Resuelve las siguiente ecuaciones
1) –6x2 +5x-1=0
2) (5x-4)(2x+3) =5
3) 30 + 9x – 3x2 =0
4) ![]()
Solución.
Multiplicamos por el M. C. M de los denominadores, que es 2(2 +x):
(2 +x)(2-x) +4.2 =2(2 +x)
4 –x2 +8 =4 + 2x,
agrupando términos y organizando la ecuación
0 = x2 +2x –8 Þ 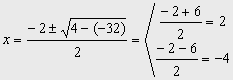
5) ![]()
6) ![]()
7) ![]()
Aplicaciones de las ecuaciones de 2º grado
Ø Ecuaciones bicuadradas
Ejemplo 8. La ecuación x4 – 5x2 +6=0 es bicuadrada (es de 4º grado sin potencias impares).
Para resolverla se procede así:
Se hace un cambio de incógnita
x2= y
con lo cual x4 = y2
Sustituyendo en la ecuación: y2-5y+6=0 que sí
es de 2º grado y podemos aplicar la fórmula: 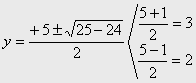
Sustituyendo los valores en la expresión x2= y , x
=![]() obtenemos:
obtenemos:
![]() y
y ![]()
En este caso la ecuación tiene 4 soluciones.
Ejercicios
Resuelve:
1) x4 –3x2+2=0
2) x4-13x2+36=0
3) x4-1=0
4) x4+ 4x2 =0
Solución.
Como es incompleta, .al igual que en las de segundo grado, sacamos factor común
x2(x2 +4) =0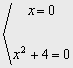 que tiene sólo la
solución (doble) x =0
que tiene sólo la
solución (doble) x =0
5) x4-9x2=0
6) 3x4 –5x2+2=0
7) x4+ x2+1=0
8)
![]()
Ø Resolución de ecuaciones irracionales.
Ejemplo
9. ![]()
Se procede de la forma siguiente:
1) Se aísla la raíz:
![]()
2) Se elevan al cuadrado ambos miembros de la igualdad:
4(x-1)=(4-x)2 Þ 4x-4 = 16-8x +x2
3) Se resuelve a ecuación de 2º grado que resulta
x2-12x +20 =0 x =10 y x =2 (comprobarlo)
4) Se comprueban las soluciones
Si x =10
![]() 16 - 4= 0 Falso, no es solución
16 - 4= 0 Falso, no es solución
Si x =2
![]() 4 - 4=0
Cierto, si es solución.
4 - 4=0
Cierto, si es solución.
Ejercicios
Resuelve las siguientes ecuaciones y comprueba las soluciones:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
Solución.
Aislamos una de las raíces: ![]()
Elevamos al cuadrado (![]()
![]()
Volvemos a aislar la raíz que nos queda
![]()
Elevamos al cuadrado
144(2x-1)=x2 +62x+961
288x -144 = x2 +62x +961
Es decir:
x2 –226x +1105 =0
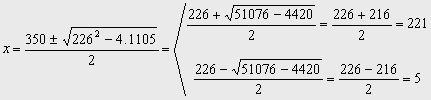
Comprobamos las soluciones:
x =221 no es solución pues
![]()
![]()
x =5 sí es solución
![]()
3=3
7) ![]()
Ecuaciones de grado superior a dos
Resolver las siguientes ecuaciones:
1) x3 –x2-x +1=0
Solución
Los divisores del término independiente son 1 y -1
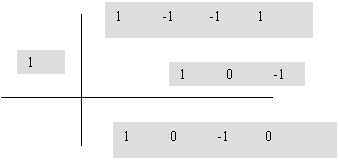 |
Luego :
x3 –x2-x +1 = (x-1)(x2-1)= (x-1)(x +1) (x-1) y las soluciones son: x =1 (doble) y x =-1
2) x4 –x3-16x2-20x = 0
3) x4-8x3+ 18x2-11x=0
4) x3-2x2-9x +18
5) x4-x3-11x2+ 9x+18=0
Sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de ecuaciones de primer grado.
Ejemplo 10: ![]() es un sistema de 2 ecuaciones con
dos incógnitas
es un sistema de 2 ecuaciones con
dos incógnitas
Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.
Hay tres métodos algebraicos para resolverlos:
ü Sustitución
Ejemplo
11. ![]()
En la 2ª ecuación despejamos la y y la sustituimos en 1ª ecuación
y =3x; 2x +3(3x) =1Þ 11x =1
Þ x =1/11
Una vez encontrado el valor de una de las incógnitas se sustituye (y =3x) para encontrar el valor de la otra incógnita: y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de, al menos, una de las incógnitas es 1.
ü Igualación
Ejemplo
12. ![]()
Despejamos la misma incógnita en las dos ecuaciones![]() ; y =3x.
; y =3x.
Igualando ![]() Þ 1-2x
=9x Þ 1= 11x Þ x =1/11
Þ 1-2x
=9x Þ 1= 11x Þ x =1/11
Ahora para obtener el valor de la y se procede como en el caso anterior, es decir se sustituye el valor hallado en la ecuación que más convenga ( en este caso en y =3x). y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de una de las incógnitas es igual en las dos ecuaciones.
ü Reducción
Ejemplo 13. ![]()
Multiplicamos la 1ª ecuación por 2 y la 2ª por 3. (De esta forma el coeficiente de y en las dos ecuaciones es el mismo, el m.c.m.
Resulta: ![]() Þ
Þ ![]()
Sumando obtenemos 13 x =2 Þ![]()
Sustituyendo el valor encontrado de x en la segunda ecuación:
![]() y =3/13
y =3/13
Nota. A veces es más cómodo usar la reducción dos veces para encontrar el valor de la otra incógnita. (Ver ejercicio resuelto).
Ø 4º Método: Resolución gráfica.
Se dibujan en los mismos ejes las dos rectas, el punto de corte es la solución del sistema.
Ejercicios
Resuelve los siguientes sistemas por el método que creas más adecuado:
1) ![]()
2) ![]()
3)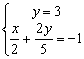
4) ![]()
5) 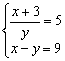
6)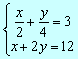
Solución
Para
quitar los denominadores multiplicamos por 4 la 1ª ecuación Þ![]()
Le resolvemos por reducción doble.
Multiplicamos
la 2ª ecuación por –2 Þ![]()
Sumando las dos ecuaciones obtenemos una equivalente: -3y = -12Þy =4
Para encontrar el valor de x, eliminamos la y, para ello multiplicando la 1ª por -2
![]() sumando –3x= -12Þ x =4
sumando –3x= -12Þ x =4
Resuélvelo gráficamente
Resolución gráfica
Resuelve gráficamente los siguientes sistemas. compruébalo analíticamente.
1) ![]()
2)![]()
Problemas de aplicación
1) Calcula dos número cuya suma sea 8 y su producto 12.
2) La suma de dos número es 65 y su diferencia 23. Halla los números
3) La diferencia de dos números es 1/6. El triple del mayor menos el doble del menor es 1. Halla dichos números.
Sistemas de ecuaciones de 2º grado
Son aquellos en que al menos una de las ecuaciones es de 2º grado. Veremos con un ejemplo como proceder para obtener las soluciones
Ejemplo 14. Sea el sistema ![]()
En la 2ª ecuación despejamos la y, y la sustituimos en la 1ª
y = 2x-4Þ 2x2+(2x –4)2=22
2x2 +4x2 –16x +16=22; 6x2-16x-6=0,
Simplificando por 2 obtenemos:3x2-8x-3=0, que es una ecuación de 2º grado completa:
![]() =
=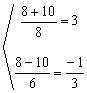
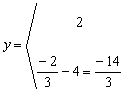
También se pueden resolver gráficamente algunos sistemas de 2º grado
Ejercicios
Resuelve los siguientes sistemas y si es posible también gráficamente:
1)
![]()
Solución
En este caso se puede resolver gráficamente. Lo haremos por tanto gráficamente como ejemplo.
La gráfica de la primera es una recta, de ecuación explícita; y =4-2x, que pasa por los puntos (0, 4) y (2, 0)
La gráfica de la segunda ecuación es una parábola.
El vértice está en el punto (0, 4) y dos puntos simétricos son los de corte con el eje de abscisas, (-2, 0) y (2, 0)
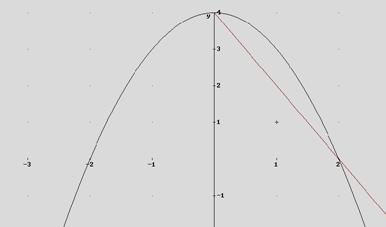
Las soluciones gráficas (0, 4) y (2, 0)
Comprobarlo resolviéndolo analíticamente.
2) ![]()
3) ![]()
3)![]()
Sistemas de tres ecuaciones con tres incógnitas,
Método de Gauss
Está basado en el de reducción. Consiste en, mediante transformaciones elementales, llegar a otro escalonado de más fácil resolución.
Ejemplo 15. Resuelve el
sistema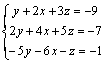
Multiplicamos la 1ª ecuación por 2 y se la restamos a la segunda:
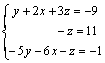
Permutamos las ecuaciones 2ª y 3ª:
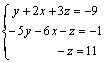
Multiplicamos la 1ª ecuación por 5 y se la sumamos a la 2ª:
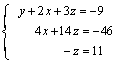
que es un sistema escalonado.
Hasta aquí es el método de Gauss, ya se ha conseguido un sistema escalonado ahora para resolverlo se procede:
z =-11, de donde
4x = -46-14(-11)Þ x=54/2, la y la obtenemos sustituyendo estos dos valores en la ecuación 1ª ;
y =-9-54+33, y=-30.
La solución es: (54/2,-30,-11)
Ejercicios
Resuelve los siguientes sistemas
1. 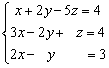
2. 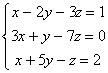
Estrategias para la resolución de Problemas.
Para resolver un problema es conveniente realizar cuatro fases[1]:
1ª. Comprender el problema.
Hay que leer el problema hasta familiarizarse con él y que podamos contestar, sin dudar, a las siguientes preguntas:
¿Cuáles son los datos? ¿cuál es la incógnita o incógnitas? ¿son las condiciones suficientes para determinar a las incógnitas? ¿son insuficientes?.. .
2ª Concebir un plan.
Determinar la relación entre los datos y la incógnitas.
De no encontrarse una relación inmediata puedes considerar problemas auxiliares.
¿Conoces problemas relacionados con éste?
¿Podrías plantear el problema de forma diferente?
¿Puedes cambiar la incógnita o los datos o ambos si fuera necesario, de tal forma que la nueva incógnita y datos estén en una relación más sencilla?...
¿Has considerado todas las nociones esenciales del problema?
.................
Obtener finalmente un plan de solución.
Para nuestro caso:
Escribir la ecuación o ecuaciones que relacionan datos e incógnitas y analizar el sistema que forman.
3ª. Ejecutar el plan.
Resuelve el sistema por los métodos estudiados.
4ª. Examinar la solución obtenida.
Comprobar si las soluciones obtenidas son válidas y proceder en consecuencia.
Problemas resueltos
1. Dos poblaciones A y B distan 25km. Un peatón sale de A hacia B a una velocidad de 4km/h. Simultáneamente sale de B hacia A otro peatón a 6km/h. Calcula el tiempo que tardan en encontrarse.
Solución
![]() A ½ B
A ½ B
![]()
![]()
25km
El espacio que recorre el peatón que sale de A es: E = v A t =4.t
El espacio que recorre el peatón que sale de B es: E = v B t = 6t
Cuando se encuentran habrán recorrido entre ambos los 25km
Por lo tanto: 4t +6t =25
10 t = 25 Þ t = 2,5 horas
Tardan en encontrarse 2 horas y media
Se encuentran a las 12 horas 16 minutos 21 segundos
2. Para vallar una finca rectangular de 750m2 se han utilizado 110m de cerca. Calcular las dimensiones de la cerca.
Solución
Llamamos x a la base del rectángulo, e y la altura.
Como la superficie es el producto de la base por la altura, entonces x .y =750
El perímetro es la suma de los 4 lados:
2x +2y =110
Es decir tenemos el sistema ![]() De la primera ecuación se
tiene y =750/x
De la primera ecuación se
tiene y =750/x
Sustituyendo en la segunda:
![]() Þ 2x2+1500
=110 x Þ 2x2-110x
+1500=0
Þ 2x2+1500
=110 x Þ 2x2-110x
+1500=0
De donde 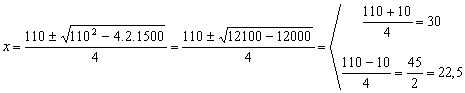
Nos da dos soluciones:
Si la base es x =30 Þ la altura es y = 750/30 =25
Si la base es x = 22,5 Þ la altura es y =750/22,5=100/3= 33,333..
Ambas válidas.
3. Un grupo de personas se reúne para ir de excursión, juntándose un total de 20 entre hombres, mujeres y niños. Contando hombres y mujeres juntos, su número resulta ser el triple del número de niños. Además, si hubiera acudido una mujer más, su número igualaría al de los hombres. ¿Cuántos hombres, mujeres y niños han ido de excursión.
Solución
Sean:
|
hombres |
x |
|
mujeres |
y |
|
niños |
z |
Luego:
x + y + z = 20
x + y = 3z Es un sistema de tres ecuaciones con tres incógnitas.
x = y + 1
Se resuelve por reducción:
Restamos a la 1º ecuación la 2ª
z =20-3z Þ 4z = 20 Þ z =5 , sustituyendo en la 2ª nos queda:
x +y =15 que junto con la 3ª forman un sistema de dos ecuaciones:
x –y =1
Sumando nos queda 2x = 16 Þ x =8 , y =7
Resuélvelo por el método de Gauss
Problemas propuestos
1. Un tendero invierte 125 € en la compra de una partida de manzanas. Desecha 20kg por defectuosas y vende el resto aumentando 0,40 € cada kilo sobre el precio de compra, por 147 €. ¿Cuántos kilos compró?
2. El perímetro de un jardín rectangular es de 68 m. Si el lado mayor mide 10 m. más que el lado menor. ¿Cuánto miden los lados del jardín?
3. Halla dos números positivos cuya suma es 20 y la suma de sus cuadrados 250.
4. Un ciclista sale por una carretera a 15km / h. Media hora después sale otro en su persecución a una velocidad de 20km/h. ¿Cuánto tardarán en alcanzarse?
5. Tres empresas aportan 2, 3 y 5 millones de euros para la comercialización de un nuevo avión. A los cinco años reparten beneficios correspondiendo a la tercera 189000 € más que a la segunda. ¿Cuál fue la cantidad repartida?
6. En la primera prueba de una oposición queda eliminado el 70% de los participantes. En la segunda queda eliminado el 40% de los restantes. Si el número de personas que aprobaron los dos exámenes fue 36 ¿cuántas personas se presentaron a la oposición?
7. Calcula tres números sabiendo que son consecutivos y que su suma es igual al cuádruple del menor.
8. La base de un rectángulo es 10cm más larga que la altura. Su área mide 600m2. Calcular las dimensiones del rectángulo.
9. Dos números son tales que el mayor menos la raíz cuadrada del menor es 22 y la suma de los números es 34. ¿Cuáles son los números.
10. Una caja mide 5cm de altura y de ancho, cinco cm. más que de largo. Su volumen es 1500cm3. Calcular la longitud y la anchura.
15. La diagonal de un rectángulo mide 26cm y el perímetro 68cm. Hallar los lados del rectángulo.
16. Los lados de un triángulo ABC miden 2, 3 y 4 m, respectivamente. Hállense lo lado de otro triángulo A’B’C’ que es semejante al anterior y tiene 36m de perímetro.
17. Calcula las edades de un padre y de sus dos hijos, sabiendo que entre los tres suman 99 años. Además se sabe que la edad del padre y la del hijo mayor difieren en 25 años, y que la suma de las edades de ambos hijos se diferencian en la edad el padre en 5 años.
Inecuaciones[2]
Para resolver las inecuaciones se utilizan las propiedades de las desigualdades:
1) si a ³ b y b ³ c Þ a ³ c
2) si a ³ b Þ a +c ³ b +c, para todo c
3) si a ³ b, y c > 0 Þ a. c ³ b. c
y c < 0 Þ a c £ b. c
A) Lineales con una incógnita
Son de la forma a. x + b £ 0 ( ³; <, ó > )
Ejemplo 1. 3x -6 <0
![]() Solución. 3x< 6 Þx<2
Solución. 3x< 6 Þx<2
|
Ejemplo 2. -2x +3> 5
![]() Solución.
-2x >5-3 =2 Þ -x>1 y x<-1
Solución.
-2x >5-3 =2 Þ -x>1 y x<-1
Haz una interpretación gráfica. -1
Ejercicios. Resuelve las siguientes inecuaciones:
1. 3x - 1![]()
2. 2x- 3 > 3x+1
B) Lineales con dos incógnitas
Una inecuación lineal con dos incógnitas es una desigualdad algebraica del tipo:
a x + by + c £ 0 ( ³; <, ó > )
Sus soluciones serán los pares de números (x, y) que hagan cierta la desigualdad.
Ejemplo 3: 2x-5y <0
(1,1) es una solución, (1,0) no lo es....
Ejemplo 1: La inecuación 2x-y > x-2y+4 es equivalente a x +y-4>0 , por tanto es lineal.
Representación gráfica del conjunto solución.
Proposición. Dada una inecuación equivalente a:
a. x + by + c > 0 ó a. x + by + c < 0
el conjunto solución es uno de los semiplanos cuya frontera es la recta:
a. x + by + c =0 (la llamaremos recta auxiliar)
La inecuación puede escribirse para b¹ 0
![]() (1)
(1)
![]() (2)
(2)
y los puntos de la recta auxiliar verifican:
![]()
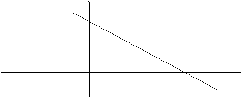 Los puntos del semiplano superior verifican (1) y los del inferior
verifican (2) (la demostración es inmediata).
Los puntos del semiplano superior verifican (1) y los del inferior
verifican (2) (la demostración es inmediata).
(1)
(2)
Ejemplo 4: Resolver gráficamente la inecuación: 2x-5y <0
Solución
 Consideramos la recta 2x-5y=0 y la representamos en el plano
Consideramos la recta 2x-5y=0 y la representamos en el plano
|
x |
y |
|
0 |
0 |
|
5 |
2 |
La recta divide al plano en dos semiplanos, en este caso, como la inecuación se puede escribir
y > ![]() , la solución es el semiplano
superior.
, la solución es el semiplano
superior.
Para señalar que no esta incluida la recta en el conjunto de las soluciones se ha dibujado ésta con trazo discontinuo. Si estuviera incluida se dibujaría con trazo continuo.
Ejercicios. Resuelve las siguientes inecuaciones lineales
1. 3x +y<2
2. x –y +1 ![]()
Sistemas de inecuaciones lineales.
*Un sistema de inecuaciones lineales es un conjunto de dos o más inecuacioness.
Resolver un sistema de inecuaciones es encontrar las soluciones comunes a todas ellas.
Con una incógnita
Ejemplo 5.
Resuelve el sistema ![]()
Solución.

![]() Þ
Þ![]()
No hay ninguna solución común, el sistema no tiene soluciones.
Ejercicios. Resuelve los siguientes sistemas de inecuaciones:
1. ![]()
2. ![]()
Con dos incógnitas
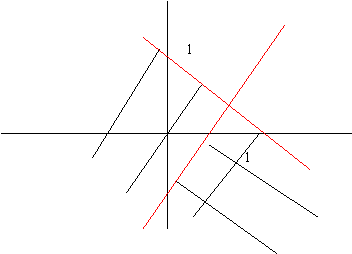 Se utilizará la representación gráfica para dar el conjunto
solución de un sistema de inecuaciones (con dos incógnitas), que será la
intersección de los semiplanos. La región del plano que determinan dichas
intersecciones se llama región factible.
Se utilizará la representación gráfica para dar el conjunto
solución de un sistema de inecuaciones (con dos incógnitas), que será la
intersección de los semiplanos. La región del plano que determinan dichas
intersecciones se llama región factible.
 Ejemplo 6. Resuelve el sistema
Ejemplo 6. Resuelve el sistema ![]()
 Solución.
Solución.
La solución es donde se cruzan
 |
|||
|
|||
Ejemplo 7
Representar gráficamente las soluciones del sistema:
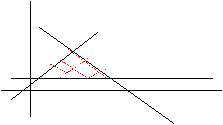 |
y £ x + 1000
x + y £3000
y ³1000
x ³0
Ejercicios. Resuelve los siguientes sistemas:
1. ![]()
2. 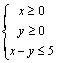
3. 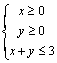
Ecuaciones exponenciales y logarítmicas
Resuelve las siguientes ecuaciones y sistemas:
1.32-x =9
Solución
32-x =32 , igualamos los exponentes 2-x =2 Þ x =0
2. 52x+1 = 1
3. ![]()
4. ![]()
5. 42x+1 = (0,5)3x+5
6. 2x +2x+2=20
Solución
2x + 4.2x=20Þ 5.2x =20Þ 2x=4 , x=2
7. 2x-1 + 2x + 2x+1 = 7.
8. 32x+2-28.3x+3=0
Solución
9.32x -28.3x+3=0, hacemos 3x =t y nos queda:
9t2-28t+3=0, ecuación de 2º grado completa
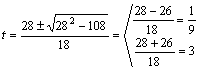
de donde 3x=1/9 Þ x =-2 ó 3x=1Þ x =1
9. 4x -3.2x+1+8=0. Indicación: 4x =22x
10. 4x-5.2x +4=0
11. 2x-1 +4x-3=5
12. 52x-30.5x+125=0
Logaritmos
Se dice que y es el logaritmo en base a de un número x (se escribe y = loga x ) , si al elevar la base a a y se obtiene dicho número x, es decir el logaritmo de un número es el exponente al que hay que elevar la base para obtenerlo:
![]()
Ejemplo: log2 8 =3 pues 23=8
Propiedades
1. loga(A.B) =logaA + logaB
2. loga(A/B)=logaA - logaB
3. logaAk =k logaA
Resuelve las siguientes ecuaciones logarítmicas:
1. log2 (2x-1)=3
Solución
(2x -1)=23Þ2x=9, x=9/2
2. ln (x2-5x+7)=0
3. log (6x-6)=log2 +log (2x+3)
Solución
log(6x-6) =log2 (2x+3)
6x-6 =4x +6Þ 2x =12, x =6
4.log (3x+1)-log (2x-3)=1-log5
5. logx(20x-4)-logx25=2
6. 2logx =1+ log (x-![]() )
)
SISTEMAS
1.![]()
Solución
Por
comodidad hacemos un cambio de variables 3x= t 3y= s, el
sistema queda ![]()
Lo
resolvemos por sustitución, s = 90 – t, de donde t(90-t)= 729 ![]() t2
-90t +729=0 sus soluciones son t =81 y t =9 (comprobarlo)
t2
-90t +729=0 sus soluciones son t =81 y t =9 (comprobarlo)
s = 90-81=9 y s = 90-9=81
Por lo
tanto para t =81, s =9 deshaciendo el cambio 3x=81![]() x = 4, 3y=9
x = 4, 3y=9 ![]() y =2
y =2
Para t
=9 , s =81 deshaciendo el cambio 3x =9 ![]() x =2, 3y =81
x =2, 3y =81 ![]() y =4
y =4
2. 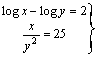
Solución
La primera ecuación se puede escribir: log (x/y) = 2, por las propiedades de los logaritmos.
Entonces: (x/y) =100 y por lo tanto x =100y
Si x/y2=25 entonces x =25y2
igualando 100y= 25y2, de donde 25y(y-4)=0, cuya única solución es y =4 (ya que y no puede ser 0) con lo cual x =400
3. ![]()
Solución
Si sumamos ambas ecuaciones obtenemos:
2log x =4 de donde log x = 2 y la x= 100 (ya que se trata de logaritmo decimal)
Sustituyendo en la segunda ecuación: 2 + log y = 3 de donde log y =-1 y por tanto y =10-1
Actividades propuestas
1. Encontrar x en cada una de las ecuaciones siguientes:
a) logx 729 = 6
b) ![]()
c) 81x = 92. 33x
d) 9x - 6. 3x+1 + 81 = 0
e) 51-x + 5x = 6
f) 2.71-x + 7x = 9
2. Calcula utilizando las propiedades de las funciones logarítmicas:
a) log 0’0001
b)![]()
c) log2 10 - log2 5
d) log2
![]()
e) log2
![]()
3. Resuelve:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Cuaderno de actividades de 1ºBach Cuaderno de 3º ESO Cuaderno 4º ESO