Observación: En esta página se hace un resumen del tema Ecuaciones y sistemas lineales para 2º Bach, Matemáticas Aplicadas a las Ciencias Sociales, también se incluye la Programación lineal. (Resolución de problemas lineales)
Si buscabas ecuaciones para la ESO te recomiendo que visites mejor esta página: Ecuaciones y Sistemas
Si buscabas el tema con más nivel, o más completo, pincha aquí: SISTEMAS LINEALES
Si tienes alguna duda, o sugerencia, visita el foro Matemáticas en el siglo XXI y deja tu mensaje
BREVE REPASO DE ECUACIONES Y SISTEMAS
Resolver una ecuación es encontrar todas sus soluciones o llegar a la conclusión de que no tiene ninguna.
Ejemplo 1. a) x2-1=0 es una ecuación de segundo grado con una incógnita, x, que tiene dos soluciones: x =1 y x =-1
b) x2 + 1=0 es una ecuación de 2º grado con una incógnita y sin soluciones en R.
c) 2x +3y = 0 es una ecuación lineal con dos incógnitas, x e y, que tiene infinitas soluciones: (0,0), (-3, 2), (3, -2)....
Ecuaciones equivalentes
Dos ecuaciones son equivalentes cuando admiten la mismas soluciones. Se cumple:
v Si se suma o resta un mismo número a los dos miembros de una ecuación, se obtiene una ecuación equivalente a la primera.
v Si se multiplican o dividen los dos miembros de una ecuación por un mismo número distinto de cero se obtiene una ecuación equivalente a la primera.
Transposición de términos. Aplicando las reglas anteriores deducimos dos reglas prácticas:
Ø Si un número aparece en un miembro sumando, se le puede pasar al otro miembro restando. Si esta restando pasará sumando.
Ø De igual manera si está multiplicando pasa dividiendo y al revés.
Esto se llama trasponer términos.
Ejemplo 2: La ecuación 5x - 1 = 2x -3 se puede escribir 3x + 2 = 0, trasponiendo términos.
Nota: El segundo miembro de la ecuación se puede considerar siempre que es 0.
Sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de ecuaciones de primer grado.
Ejemplo 1:
![]() es un sistema de 2 ecuaciones con dos
incógnitas
es un sistema de 2 ecuaciones con dos
incógnitas
Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.
Ejemplo 2. 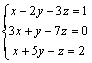 es un sistema de 3 ecuaciones con tres incógnitas
es un sistema de 3 ecuaciones con tres incógnitas
Clasificación de sistemas.
Si el sistema tiene solución se dice compatible. Si la solución es única se dice determinado y en otro caso indeterminado. Si no tiene solución se dirá incompatible.
Es decir se clasifican, según el número de soluciones en:
|
· Compatibles · Incompatibles (ninguna solución) |
Ejemplo 3. El sistema:
![]() es
incompatible.
es
incompatible.
Sistemas de dos ecuaciones con dos incógnitas (repaso)
Hay tres métodos algebraicos para resolverlos: sustitución, igualación y reducción
Ejemplo
2. ![]()
Multiplicamos la 1ª ecuación por 2 y la 2ª por 3. (De esta forma el coeficiente de y en las dos ecuaciones es el mismo, el m.c.m.
Resulta: ![]() Þ
Þ ![]()
Sumando obtenemos 13
x =2 Þ![]()
Sustituyendo el valor encontrado de x en la segunda ecuación:
![]() y =3/13
y =3/13
Nota. A veces es más cómodo usar la reducción dos veces para encontrar el valor de la otra incógnita.
Sistemas de ecuaciones con tres (o más) incógnitas
Definición 1. Dos sistemas de ecuaciones lineales son equivalentes si tienen el mismo conjunto de soluciones.
El método general de resolver sistemas de ecuaciones consiste en encontrar otro sistema equivalente de más fácil resolución.
Definición 2. Se llaman transformaciones elementales (o de equivalencia) a aquellas modificaciones de un sistema lineal que lo transforman en otro equivalente.
Proposición.
Las siguientes transformaciones son elementales.
1) Permutar dos ecuaciones.
2) Multiplicar una ecuación del sistema por un número distinto de 0.
3) Sumar a una ecuación del sistema otra multiplicada por un número.
4) Cambiar el orden de las incógnitas.
5) Despejar una incógnita en una ecuación y sustituirla en las demás ecuaciones.
6) Suprimir o añadir una ecuación que sea combinación lineal de las otras.
La demostración es inmediata en todos los casos.
Método de Gauss
El método de Gauss para la resolución de sistemas lineales se puede considerar como un generalización del de reducción (para los sistemas con dos o tres incógnitas). En esencia consiste en hacer, al sistema de ecuaciones lineales, determinadas transformaciones elementales a fin de obtener un sistema escalonado, más fácil de resolver.
.
Ejemplo 3. Resuelve el
sistema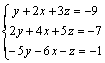
Multiplicamos la 1ª ecuación por 2 y se la restamos a la segunda:
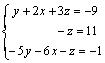
Permutamos las ecuaciones 2ª y 3ª:
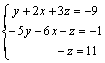
Multiplicamos la 1ª ecuación por 5 y se la sumamos a la 2ª:
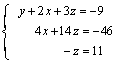
que es un sistema escalonado.
Hasta aquí es el método de Gauss[1], ya se ha conseguido un sistema escalonado ahora para resolverlo se procede (de abajo arriba):
z =-11, de donde
4x = -46-14(-11)Þ x =54/2, la y la obtenemos sustituyendo estos dos valores en la ecuación 1ª ;
y =-9-54+33, y =-30.
La solución es: (54/2,-30,-11)
Ejercicios
Resuelve los siguientes sistemas
1. 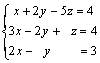 2.
2.
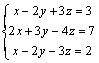
3.
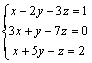 4.
4. 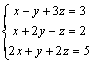
Forma matricial del método de Gauss (veremos un ejemplo)
Resuelve el sistema 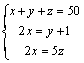
Se consideran solo los coeficientes colocándolos así 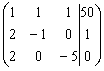 y
se trata de conseguir que todos los elementos por debajo de la diagonal
principal sean cero (ver enlace de abajo para la justificación teórica del
método)
y
se trata de conseguir que todos los elementos por debajo de la diagonal
principal sean cero (ver enlace de abajo para la justificación teórica del
método)
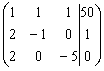
![]()
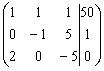
![]()
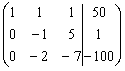
![]()
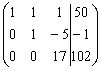 ....
....
El sistema que nos queda ahora es escalonado y de más fácil resolución:
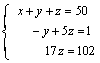
![]()
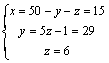
Comprueba los resultados
SI QUIERES MAS EJERCICIOS O MÁS NIVEL EN EL TEMA DE SISTEMAS LINEALES PINCHA AQUÍ
Significado geométrico de las ecuaciones y sistema lineales[2].
I) Significado geométrico de las ecuaciones lineales
Las soluciones de las ecuaciones lineales de 2 y 3 incógnitas pueden interpretarse de un modo geométrico en el plano y en espacio tridimensional, respectivamente.
1) La ecuación ax + by +c = 0, como se ha visto en cursos anteriores, representa una recta en el plano afín. Un vector de dirección es (b, -a) y la pendiente de la recta (el coeficiente de la x) es:
m =-a/b
Si
hacemos x = t, quedaría ![]() , que podemos escribir:
, que podemos escribir:
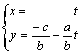
“Son las ecuaciones paramétricas de la recta que pasa por el punto (0,-c/b) y (1,-a/b) es un vector de dirección.”
Ejemplo 4. Las ecuaciones paramétricas de la recta 6x - 2y + 5 = 0, son:
![]() ,
pasa por el punto (0,5/2), y u n vector de dirección
es (1,3) .
,
pasa por el punto (0,5/2), y u n vector de dirección
es (1,3) .
2) En el espacio tridimensional real la ecuación :
ax + by + cz + d = 0, representa un plano.
En efecto, como, para determinar un plano hay que conocer:
1) un punto por el que pase
2) dos vectores de dirección (vectores l. independientes contenidos en el plano)
Si
hacemos x = t, y = s, nos quedaría: 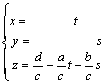 ,
,
Son las llamadas ecuaciones paramétricas del plano que pasa por (0, 0, d/c) y tiene por vectores de dirección a (-b/a,1 ,0) y a (-c/b, 0, 1).
Podemos pues concluir que toda ecuación lineal de tres incógnitas representa un plano.
Ejemplo 5. Vamos a encontrar las ecuaciones paramétricas del plano, solución de la ecuación lineal: 2x - 3y + z =1.
Solución:
Si hacemos x = t, e y = s, quedaría z = 1 - 2t + 3s.
esta
ecuación se puede escribir: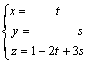 ,
,
que son las ecuaciones del plano que pasa por el punto P(0,0,1) y tiene como vectores de dirección a v(1,0,-2) y w(0,1,3).
Ejercicio. Hallar las ecuaciones paramétricas de los planos siguientes:
a) x = 2;
b) 2x + z = 0;
c) y =-3
d) 2x-4y +2z -1 =0
e) y-2z = 3
II) Significado geométrico de los sistemas.
Al igual que en las ecuaciones lineales, consideramos la interpretación geométrica en el plano (sistemas de ecuaciones con dos incógnitas) y en espacio (sistemas de ecuaciones con tres incógnitas).
♦ Sistemas de ecuaciones lineales con dos incógnitas.
Posiciones relativas de rectas en el plano.
a) Si el sistema es compatible determinado (es decir, solución única), las rectas se cortan. El punto de corte es la solución del sistema.
Ejemplo 6. Las rectas
3x +y =5 y 2x – y =3, son secantes , pues tienen distinta pendiente. El punto de corte lo encontramos al resolver
el sistema ![]() (hacerlo)
(hacerlo)
b) Si el sistema es incompatible las rectas no tienen ningún punto en común, son paralelas.
En tal caso los vectores de dirección son proporcionales.
c) Cuando el sistema es compatible indeterminado se trata de la misma recta.
Ejercicio[3]. Dados los puntos del plano (1, 1) y (3, -2), se pide: a) Encontrar de forma razonada la ecuación de la recta que pasa por ambos puntos, b) deducir si dicha recta es paralela o si corta a la recta de ecuación 3x +y =5 y, c) en este último caso, calcular el punto de corte.
♦ Sistemas de ecuaciones lineales con tres incógnitas.
A) Sistemas de 2 ecuaciones con 3 incógnitas.
La resolución del
sistema: ![]()
en términos geométricos es el estudio de las posiciones relativas de dos planos, casos que se presentan:
■ Planos paralelos. Sin puntos comunes, cuando el sistema sea incompatible.
● Planos que se cortan en una recta. Si el sistema es compatible pero indeterminado, con un grado de libertad.
■ Planos coincidentes. Ocurre este caso cuando las dos ecuaciones son equivalentes y el sistema es compatible indeterminado con dos grados de libertad
B) Sistemas de tres ecuaciones con tres incógnitas:
![]()
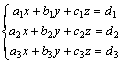
Cada ecuación representa un plano en el espacio tridimensional. Luego se trata de estudiar la posición relativa de tres planos en el espacio. Las soluciones del sistema son geométricamente los puntos de intersección de los tres planos, los casos son:
▲ Un punto único. Sistema compatible determinado.. Los tres planos se cortan en P.
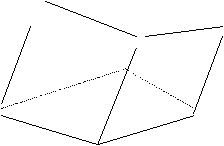 |
p
· Una recta. Son soluciones todos los puntos representativos de la recta común. Sistema compatible indeterminado con un grado de libertad.
Los planos se cortan en r.
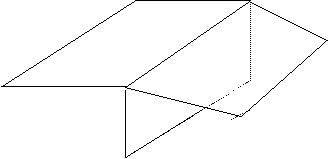
r
▼ Un plano. Los planos son coincidentes. El sistema es compatible indeterminado con dos grados de libertad.
◄ Ningún punto. El sistema es incompatible. Esta situación se presenta geométricamente de distintas maneras. Para estudiar las posiciones relativas de los planos hay que tomarlos de dos en dos.
Se pueden presentar varios casos: Que los planos sean paralelos:
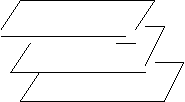 P1
P1
P2
P3
Ejercicio . Estudiar los demás casos (hay otros tres).
Ejercicios
1) Interpreta geométricamente las soluciones de los siguientes sistemas:
a) 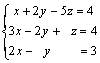 b)
b)
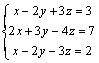
2) Calcula k para que los planos siguientes se corten en una recta.
x + y + z = 2
2x + 3y + z = 3
kx + 10y + 4z =11
3) Hállense todos los valore posibles de a, b, y c para que los planos siguientes sean paralelos o coincidentes:
x + by + 5cz =1
2x + (a-1)y + (3b-1)z =2
b) ¿Para qué valores específicos de a, b y c los dos planos anteriores son coincidentes y pasan por el punto (1,2,-1)
Solución: Por la condición de paralelismo:
1/2 = b/(a-1) = 5c/(3b - 1) = 1/2; serían coincidentes.
Se tiene: 1/2 = b/(a-1), de donde a -1 = 2b Þ a - 2b - 1 =0
1/2 = 5c/(3b - 1) Þ 3b -1 = 10c Þ 3b - 10c -1 =0
El
sistema es indeterminado, si hacemos b = t, nos queda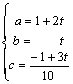 [1]
[1]
b) Si queremos que además pasen por (1, 2, -1) se tendrá:
1 + 2t - (-1 +3t)/2 = 1, de donde t = -1,
Sustituyendo en [1] se obtiene: a = -1, b = -1, c = -2/5.
Estrategias para la resolución de problemas lineales.(ver este enlace)
Problemas modelos
1. Alejandra tiene 27 años más que su hija Carmen. Dentro de 8 años, la edad de Alejandra doblará a la de Carmen. ¿Cuántos años tiene cada una?
Solución
1º. Comprender el problema.
Es un problema con dos incógnitas y dos condiciones, luego suficientes para poder determinarlas. Llamamos x a la edad de Alejandra e y a la de su hija.
Ordenamos los elementos del problema:
|
|
Hoy |
dentro de 8 años |
|
La madre |
x |
x + 8 |
|
La hija |
y |
y + 8 |
2º. Concebir un plan.
Escribimos las ecuaciones que relacionan los datos con las incógnitas:
x = 27 + y x + 8 = 2(y +8)
Es un sistema lineal de dos ecuaciones con dos incógnitas. Lo resolveremos por el método de sustitución.
3º Ejecutar el plan. x = 27 + y
Entonces: 27 + y +8 = 2(y +8) de donde 35 -16 = y Þ y = 19, x = 46
4º Examinar la solución obtenida .
La solución obtenida es factible por ser entera. El método empleado se puede usar en problemas “similares”.
Nota. En los demás problemas el alumno indicará las cuatro fases.
2. Un grupo de personas se reúne para ir de excursión, juntándose un total de 20 entre hombres, mujeres y niños. Contando hombres y mujeres juntos, su número resulta ser el triple del número de niños. Además, si hubiera acudido una mujer más, su número igualaría al de los hombres. ¿Cuántos hombres, mujeres y niños han ido de excursión.
Solución . Sean:
|
hombres |
x |
|
mujeres |
y |
|
niños |
z |
Luego:
x + y + z = 20
x + y = 3z Es un sistema de tres ecuaciones con tres incógnitas.
x = y + 1 Se resuelve por reducción:
Restamos a la 1º ecuación la 2ª
z =20-3z Þ 4z = 20 Þ z =5 , sustituyendo en la 2ª nos queda:
x +y =15 que junto con la 3ª forman un sistema de dos ecuaciones:
x –y =1
Sumando nos queda 2x = 16 Þ x =8 , y =7
Otra forma
![]()
![]() Utilizando el
método de Gauss .
Utilizando el
método de Gauss .
![]()
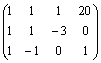 Þ
Þ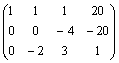 Þ
Þ Þ
Þ
El sistema que resulta es:
x + y + z = 20
-2 y + 3z = 1
z = 5
Sustituyendo en la 2º ecuación
2y = 3z-1 = 14 Þ y =7
Sustituyendo los valores hallados en la 1ª ecuación:
x = 20 –y –z = 20-7-5=8
3. Lewis Carroll, autor de Alicia en el país de las maravillas, propone un problema que puede enunciarse así: el consumo en una cafetería de un vaso de limonada, tres sandwiches y siete bizcochos ha costado 1 chelín y 2 peniques, mientras que un vaso de limonada, cuatro sandwiches y diez bizcochos vale 1 chelín y 5 peniques. Hallar cuál es el precio:
1º) De un vaso de limonada, un sandwich y un bizcocho.
2º) De dos vasos de limonada, tres sandwiches y cinco bizcochos.
Resolver el problema recordando que 1 chelín vale 12 peniques.
Solución
Es un problema con tres incógnitas y sólo dos condiciones, luego los valores de las incógnitas no se podrán determinar.
Llamamos : x al precio de un vaso de limonada, y al de un sándwich y z al de un bizcocho.
Entonces: x + 3y + 7z = 14 (peniques)
![]() x + 4y + 10z
= 17
x + 4y + 10z
= 17
![]() Lo resolvemos por Gauss:
Lo resolvemos por Gauss:![]() Þ
Þ![]()
el sistema escalonado es: x + 3y + 7z = 14 (peniques)
y + 3z = 3,
que tiene menos ecuaciones que incógnitas. Es por tanto un sistema compatible indeterminado, con un grado de libertad.
Haciendo z =t, nos queda x = 5 + 2t, y = 3 - 3t ,
Encontremos los precios de las combinaciones que nos piden.
1º) x + y + z = (5 + 2t) + (3 - 3t) + t =8 peniques. (no depende de t)
2º) 2x + 3y + 5z = 10 + 4t + 9 -9t +5t= 19 peniques. “
Si necesitas más problemas visita Ejercicios modelos, ó Selectividad LOGSE
ANEXO
Ecuaciones de la recta en el plano.
La “ecuación de la recta” expresa la condición que deben de cumplir sus puntos para pertenecer a ella. Hay distintas formas de dar la ecuación de una recta. Dependiendo de lo que conozcamos o para qué la necesitemos usamos una u otra forma de dar la recta. Veremos las mas usadas.
Ya en otros cursos se han trabajado con rectas y se han usado distintas nombres para sus ecuaciones:
- ecuación “explicita” y = mx +n.
-ecuación “implícita, general o cartesiana” que viene dada por la expresión: ax +by +c = 0.
-ecuación punto pendiente de la recta y-y0 =m(x-x0) (se usa sobre todo en derivadas, en estadística bidimensional, en interpolación lineal.).
En ellas se tiene determinada la pendiente de la recta m (en la implícita m = -a/b).
Ejercicios.
1. Hallar las ecuaciones de la recta que pasa por los puntos A(2, -1) y B(2, 3) en todas las formas que conozcas.
2. Encuentra la ecuación de la recta que pasa por el punto A(-1, 3) y es paralela a la recta
2x +y =1
Ecuaciones vectorial y paramétricas:
-
Recta que pasa por el punto A(a1, a2) y tiene de vector
dirección ![]() )
)
![]()
![]() ecuación
vectorial
ecuación
vectorial

![]() X En coordenadas
(x1, x2)= (a1, a2)+ t(v1,
v2) y:
X En coordenadas
(x1, x2)= (a1, a2)+ t(v1,
v2) y:
A x1 =a1+ t v 1
x2 = a2+ t v2 ecuaciones paramétricas
Ejemplo 1: la ecuación vectorial de la recta que pasa por el punto (2, -1) y tiene el vector de dirección (3, 4) es:
O (x, y) = (2, -1)+t(3,4)
Las ecuaciones paramétricas: ![]()
Ecuación continua
Si eliminamos el parámetro t, obtenemos:
![]() que se llama
ecuación continua de la recta.
que se llama
ecuación continua de la recta.
Ejemplo 2: la ecuación continua de la recta que pasa por (2, -1) y tiene como vector de dirección (3, 4) :
![]()
Ecuación cartesiana
v2(x1-a1)=v1(x2-a2) v2x1 –v1x2-v2a1 +v1a2=0, que se puede escribir A x + B y + C = 0 (....)
POSICIÓN RELATIVA DE RECTAS
Si dos rectas tienen la misma dirección se dice que son paralelas. Cuando no son paralelas se cortarán en un punto, se dicen secantes. Dos rectas pueden ser secantes o paralelas.
Si son paralelas tienen la misma pendiente.
Se puede determinar una recta conociendo uno de sus puntos y una paralela a ella. Hay varias formas de determinar este tipo de rectas, depende el método de cómo te den la paralela.
Ejemplo. Calcula la recta que pasa por el punto A(0, 3) y es paralela a la recta 2x-3y-4= 0.
En este caso consideramos el haz de rectas paralelas a 2x-3y-4=0 que es 2x-3y+ c = 0, donde c es una constante. Determinando c obtendremos la recta del haz que pasa por A.
Como pasa por A, este punto tiene que verificar la ecuación: 2.0-3.3+ c =0, c =9, y la recta 2x-3y+9=0
Ejercicios
1. a) Encuentra la ecuación de la recta r que pasa por los puntos A(-1, 3) y B(2, 2).
b) Halla la pendiente de r.
2. Encuentra la ecuación de la recta que pasa por el punto A(-1, 3) en todas las formas que conozcas.
Encuentra la paralela a la recta 2x +y =1 y que pase por A.
3. Dados los puntos del plano (1, 2) y (-3, 1), se pide: a) Encontrar de forma razonada la ecuación de la recta que pasa por ambos puntos, b) deducir si dicha recta es paralela o si corta a la recta de ecuación x +4y =5 y, c) en este último caso, calcular el punto de corte.
LOS TEMAS SIGUIENTES DEl ÁLGEBRA TE LOS PUEDES DESCARGAR EN LAS SIGUIENTES PÁGINAS
Programación lineal
INTRODUCCIÓN
La programación lineal como método de optimación
La complejidad de nuestra sociedad en cuanto a organización general y económica exige disponer de métodos para la planificación y organización de la industria, de los transportes y para la asignación de trabajos en forma óptima. La programación lineal (iniciada por Dantzig en 1947), que es una pequeña parte de todo un cuerpo matemático que se ha venido consolidando en el siglo XX con el nombre de optimización, abarca métodos de resolución de problemas en los que se buscan los valores máximos o mínimos de funciones del tipo:
f = a 1x 1 + a 2x 2+....+ a nx n (llamada función objetivo )
cuyas variables x 1,x2,...,xn están sujetas a unas condiciones restrictivas que se expresan por medio de desigualdades.
Estudiaremos en esta unidad sólo el caso de dos variables y para su resolución métodos gráficos.
Ejemplo de un problema tipo de programación lineal
Una empresa fabrica dos clases de lápices. De la clase A a 0,20 €. la unidad y de la clase B a 0,15 €.. unidad.
En la producción diaria se sabe que: el número de la clase B no supera en 1000 unidades a los de A; entre las dos clases no superan a 3000 unidades y los de la clase B no bajan de 1000 unidades. Hallar el costo máximo y mínimo de la producción diaria.
Vamos a traducir el enunciado al lenguaje algebraico:
Sea x el número de unidades fabricadas por día de la clase A
Sea y el número de unidades fabricadas por día de la clase B
el beneficio obtenido al vender x unidades de A e y envases de B será :
20x + 15y, entonces consideramos la función
f(x,y)= 20x + 15y ,
que llamaremos función objetivo, y queremos hallar x, y para que sea máximo o mínimo; x e y están sujetas a las siguientes condiciones (restricciones) :
y £ x + 1000
x + y £ 3000, y ³ 1000
Además debe ser:
x ³ 0
Por tanto el problema consiste en hallar x, y de forma que el valor
f = 0,20x + 0,15y ( función objetivo ) sea máximo con las condiciones:
y £ x + 1000
x + y £ 3000
y ³1000
x ³0
El conjunto de puntos que cumplen estas condiciones se llama conjunto de puntos factibles ( o región factible).
La solución factible que haga óptima la función objetivo se llama solución óptima.
Para resolver el problema aplicaremos lo que estudiamos en el tema de inecuaciones, en 1º Bach
Inecuaciones (repaso)
Para resolver las inecuaciones se utilizan las propiedades de las desigualdades:
1) si a ³ b y b ³ c Þ a ³ c
2) si a ³ b Þ a +c ³ b +c, para todo c
3) si a ³ b, y c > 0 Þ a. c ³ b. c
y c < 0 Þ a c £ b. c
A) Lineales con una incógnita
Son de la forma a. x + b £ 0 ( ³; <, ó > )
Ejemplo 1. 3x -6 <0
![]() Solución. 3x< 6 Þx<2
Solución. 3x< 6 Þx<2
|
Ejemplo 2. -2x +3> 5
![]() Solución. -2x >5-3 =2 Þ -x>1 y x<-1
Solución. -2x >5-3 =2 Þ -x>1 y x<-1
Haz una interpretación gráfica. -1
Ejercicios. Resuelve las siguientes inecuaciones:
1.
3x - 1![]()
2. 2x- 3 > 3x+1
B) Lineales con dos incógnitas
Una inecuación lineal con dos incógnitas es una desigualdad algebraica del tipo:
a x + by + c £ 0 ( ³; <, ó > )
Sus soluciones serán los pares de números (x, y) que hagan cierta la desigualdad.
Ejemplo 3: 2x-5y <0
(1,1) es una solución, (1,0) no lo es....
Ejemplo 1: La inecuación 2x-y > x-2y+4 es equivalente a x +y-4>0 , por tanto es lineal.
Representación gráfica del conjunto solución.
Proposición. Dada una inecuación equivalente a:
a. x + by + c > 0 ó a. x + by + c < 0
el conjunto solución es uno de los semiplanos cuya frontera es la recta:
a. x + by + c =0 (la llamaremos recta auxiliar)
La inecuación puede escribirse para b¹ 0
![]() (1)
(1) ![]() (2)
(2)
y los puntos de la recta auxiliar verifican:
![]()
 Los puntos del semiplano
superior verifican (1) y los del inferior verifican (2) (la demostración es
inmediata).
Los puntos del semiplano
superior verifican (1) y los del inferior verifican (2) (la demostración es
inmediata).
(1)
(2)
Ejemplo 4: Resolver gráficamente la inecuación: 2x-5y <0
Solución
 Consideramos la recta 2x-5y=0
y la representamos en el plano
Consideramos la recta 2x-5y=0
y la representamos en el plano
|
x |
y |
|
0 |
0 |
|
5 |
2 |
La recta divide al plano en dos semiplanos, en este caso, como la inecuación se puede escribir
y > ![]() , la
solución es el semiplano superior.
, la
solución es el semiplano superior.
Para señalar que no esta incluida la recta en el conjunto de las soluciones se ha dibujado ésta con trazo discontinuo. Si estuviera incluida se dibujaría con trazo continuo.
Ejercicios. Resuelve las siguientes inecuaciones lineales
1. 3x +y<2
2.
x –y +1 ![]()
Sistemas de inecuaciones lineales.
*Un sistema de inecuaciones lineales es un conjunto de dos o más inecuaciones.
Resolver un sistema de inecuaciones es encontrar las soluciones comunes a todas ellas.
Con dos incógnitas
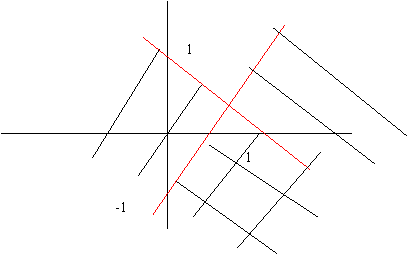 Se utilizará la representación
gráfica para dar el conjunto solución de un sistema de inecuaciones (con dos
incógnitas), que será la intersección de los semiplanos. La región del plano
que determinan dichas intersecciones se llama región factible.
Se utilizará la representación
gráfica para dar el conjunto solución de un sistema de inecuaciones (con dos
incógnitas), que será la intersección de los semiplanos. La región del plano
que determinan dichas intersecciones se llama región factible.
Ejemplo 6. Resuelve el sistema ![]()
Solución.
La solución es donde se cruzan
Ejemplo 7
Representar gráficamente las soluciones del sistema:
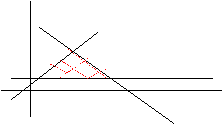 |
y £ x + 1000
x + y £3000
y ³1000
x ³0
Ejercicios. Resuelve los siguientes sistemas:
1.
![]() 2.
2. 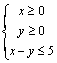 3.
3. 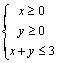
La función objetivo y la programación lineal.
Como ya hemos indicado en la introducción los problemas de programación lineal consisten en hallar los valores óptimos (máximo o mínimo) de una función del tipo
f(x, y)= ax + by + c, llamada función objetivo, cuando las variables están sujetas a unas condiciones que vienen expresadas por inecuaciones lineales y eventualmente también por ecuaciones lineales. Dichas condiciones se denominas las restricciones.
Resolución de problemas de programación lineal. Método gráfico.
Como ya se ha comentado para el nivel de este curso sólo se estudiará el método gráfico, que expongo a continuación:
Consideremos el problema de obtener el valor máximo y mínimo de una función lineal
f = ax + by sujeta a las restricciones:
R: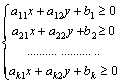
Una vez representada gráficamente la región factible R, es decir, la solución del sistema de restricciones, como queremos que f sea óptima en R representamos sobre los mismos ejes la recta:
ax + by = 0 (3),
Todas las rectas ax + by = k son paralelas a (3), y mas alejadas de ella cuanto mas aumenta k, por lo tanto elegiremos la paralela a ella, con las siguientes condiciones:
-Ha de pasar por alguno de los puntos factibles (ese punto tendrá las coordenadas buscadas)
-Debe estar lo más alejada posible a (3) si buscamos el máximo, o la más próxima si buscamos un mínimo.
Pondremos algunos ejemplos resueltos que ayudarán a entender el método.
Ejemplo 1.
![]() Hallar el máximo de la función
objetivo sujeta a las restricciones:
Hallar el máximo de la función
objetivo sujeta a las restricciones:
y³ 0
 y£x
y£x
y£ 2 - x
![]()
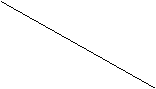 Solución
Solución
![]()
![]() Dibujamos las rectas auxiliares:
2x +3y=5
Dibujamos las rectas auxiliares:
2x +3y=5
![]()
![]()
![]()
![]()
![]()
![]()
![]() y =0, y =x, y =2-x
y =0, y =x, y =2-x
y la región factible que es la parte rayada.
Representamos la recta 2x +3y=0, y las paralelas a ella se observa que la mas alejada es la que toca a R en el punto (1,1), luego el valor máximo es 5 y se alcanza en el (1,1), que es un vértice de R.
Ejemplo 2. Averiguar si la función lineal f = x + 4y tiene máximo y mínimo sobre el conjunto solución de :
y - x ³ -3
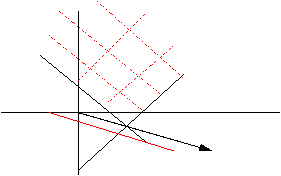
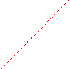 y + x ³ 1
y + x ³ 1
Solución
Dibujamos el conjunto solución:
-(-2,-1)
es el área rayada. Vemos que no está acotado.
En el gráfico está dibujada la recta x + 4y = 0 y el haz de rectas paralelas a la misma, observamos que k puede tomar el valor tan grande como se quiera, por lo que no existe el máximo de f en ese conjunto. El mínimo se alcanza en el único punto extremo (2,-1) en que f vale -2.
Pasos para resolver un problema de programación lineal en el plano.
Los siguientes "pasos" resumen como resolver un problema de p.l. en el plano
Paso 1. Identificar las variables del problema.
Paso 2. Confeccionar una tabla que resuma la información facilitada.
Expresar las restricciones o limitaciones dadas en el problema mediante
un sistema de desigualdades relativo a las variables.
Paso 3. Representación gráfica del sistema de desigualdades, determinando el llama-
do conjunto factible.
Paso 4. Establecer la función objetivo lineal, que deberá ser maximizada o minimizada.
Paso 5. Resolver el problema planteado.
Paso 6. Interpretar los resultados.
Ejemplo 3. Una fábrica de tejidos tiene almacenados 3600 m de tela blanca, 2340 m de tela roja y 1500 m de tela azul. Para distribuirlas a las sastrerías las empaquetan de dos formas A y B:
paquete A: 30m de tela blanca, 18 de tela roja y 10 de tela azul
paquete B: 20m de tela blanca, 15 roja y 10 azul.
El paquete A cuesta 13500 pta. y el B cuesta 11000 pta. ¿Cuántos paquetes debe hacer de cada tipo para maximizar los ingresos?.
Solución
Paso 1.
Llamamos x al número de paquetes de tipo a e y al número de paquetes de tipo B.
Paso 2.
|
nº blanca roja azul |
|
paquete A x 30x 18x 10x |
|
paquete B y 20y 15y 10y |
|
totales 3600 2340 1500 |
Restricciones
30x + 20y < 3600 R1
18x + 15y < 2340 R2
10x + 10y < 1500 R3
Además cómo el número de paquetes no puede ser negativo se tiene:
x > 0
y > 0
Paso 3. Dibujamos las rectas auxiliares, r1, r2, r3
![]()
![]()
![]()
![]()
![]()
![]() x
y x y x y
x
y x y x y
0 180 0 156 0 150
120 0 130 0 150 0
puntos de corte de r1 puntos de corte de r2 puntos de corte de r3
(para no tener que repetir la región factible la pongo sólo en el paso 5)
Paso 4. La función objetivo es:
f(x, y) = 13500x + 11000y
que debe ser maximizada.
Paso 5. Utilizando regla y cartabón se localiza el vértice de la región factible más alejado; es el (60,80).
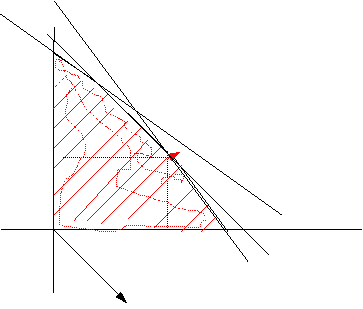
(0,150)
(30,120)
(80,60)
(0.0) (120,0)
Paso 6.
La solución es 80 paquetes de A y 60 paquetes de B.
Teorema fundamental y cálculo analítico de soluciones.
Sólo se dejará usar este método como comprobación de la solución, en los caso de que debido a las condiciones del problema (por ejemplo vértices muy próximos) puedan surgir dudas.
Teorema. Si R es un conjunto acotado de soluciones de un sistema de inecuaciones lineales (conjunto poligonal convexo) con dos incógnitas los valores máximo y mínimo de f, función objetivo, se alcanzan en puntos extremos.
Teniendo en cuenta el teorema anterior para resolver un problema de programación lineal, por el método analítico, haremos lo siguiente:
1) Dibujar la región factible R y ver si está acotada.
2) Hallar los vértices de R.
3) Calcular los valores de f en estos puntos extremos.
El valor máximo de f en estos puntos es el máximo de f en R. el mínimo de f en estos puntos es el mínimo de f en R.
Ejemplo 4. Resolveremos el ejercicio planteado en la introducción al tema.
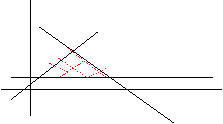 La función objetivo es en este
caso
La función objetivo es en este
caso
f = 20x +15y
La región factible es
y £ x + 1000
x + y £3000
y ³1000
x ³0
Los extremos de R son A(0,1000), B(1000,2000), y C(2000,1000).
El valor de f en esos puntos es:
f(0,1000)=15000 , f(1000,2000)=50000, f(2000,1000)=55000, luego el valor máximo de f es 55000 y el mínimo 15000.
Ejemplo 5. Una persona para recuperarse de una cierta enfermedad tiene que tomar en su alimentación dos clases de componentes que llamaremos A y B. Necesita tomar 70 unidades de A y 120 unidades de B. El médico le da dos tipos de dietas en las que la concentración de dichos componentes es:
dieta D1: 2 unidades de A y 3 unidades de B
dieta D2: 1 unidad de A y 2 unidades de B.
Sabiendo que el precio de la dieta D1 es 2,5 €. y el de la dieta D2 es 1,45 €. ¿cuál es la distribución óptima para el menor coste?
Solución:
 Lo resolveremos gráficamente.
Lo resolveremos gráficamente.
Sean x e y el número de dietas D1 y D2 respectivamente.
La función objetivo es:
C(x,y) = 2,5 x + 1,45 y
Las restricciones son :
2x + y ³ 70
3x + 2y ³ 120 ·(20,30)
x ³ 0 , y³ 0
![]()
![]() x y
x y
![]() 0 0
0 0
29 -50
Los vértices de la región factible son: (0,0),(0,60), (20,30) y (40,0)
Se observa en el gráfico que la solución óptima es 20 D1 y 30 dietas D2.
Comprobarlo analíticamente.
Si necesitas más problemas resueltos visita estas páginas:
Ejercicios Programación lineal
Problemas propuestos
1. El INSERSO debe organizar un viaje para 800 personas con cierta empresa que dispone de 16 autobuses de 40 plazas cada uno y 20 autobuses de 50 plazas cada uno. El alquiler de un autobús pequeño cuesta 3000 ptas y el alquiler de un autobús grande cuesta 4000ptas.
Averiguar razonadamente cuántos autobuses de cada clase hay que contratar para minimizar el coste y cuál sería el mínimo coste, sabiendo que la empresa solo dispone de 18 conductores.
2. La función f(x ,y)= 2x +3y está definida en el polígono de vértices (0,0), (6,0), (6,8), (4,12) y (0.15). Determinar de forma razonada todos los puntos en los que la función f alcanza un máximo. Justificar de forma razonada si dicho máximo se alcanza en un solo punto o no. ¿En qué punto o puntos se alcanza el máximo? ¿Cuál es el valor máximo?
3.Una industria fabrica bolígrafos que vende .a 400ptas cada uno y plumas estilográficas que vende a 1200ptas. cada una. Las máquinas limitan la producción de manera que cada día no se pueden producir mas de 200 bolígrafos ni más de 150 plumas estilográficas, y el total de la producción (bolígrafos mas plumas) no puede superar las 250 unidades. La industria vende siempre toda la producción. Deduzca razonadamente cuántos bolígrafos y plumas estilográficas ha de producir al día para maximizar el beneficio y cuál sería aquel.
4. Una fábrica produce lámparas normales a 9 € cada una y focos halógenos a 12 € cada uno. La capacidad máxima diaria de fabricación es de 1000, entre lámparas normales y focos halógenos, si bien, no se pueden fabricar más de 800 lámparas normales ni más de 600 focos halógenos.
Se sabe que la fábrica vende toda la producción. Averiguar de forma razonada cuánta lámparas y cuántos focos ha de producir para obtener la máxima facturación posible y cuál seria ésta.
5. Se considera la región factible dada por el siguiente conjunto de restricciones:
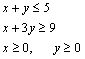
Representar la región factible que determina el sistema de inecuaciones anterior y hallar de forma razonada el punto o puntos de la región factible donde las siguientes funciones alcanzan su máximo y mínimo: a) f(x, y)=2x +3y,
b) f(x, y)=y – x
6. Se dispone de 120 refrescos de cola con cafeína y de 180 refrescos de cola sin cafeína. Los refrescos se venden en paquetes de dos tipos. Los paquetes de tipo A contienen tres refrescos con cafeína y tres sin cafeína, y los de tipo B contienen dos con cafeína y cuatro sin cafeína. El vendedor gana 6 euros por cada paquete que venda de tipo A y 5 euros por cada uno que vende de tipo B. Calcular de forma razonada cuántos paquetes de cada tipo debe vender para maximizar los beneficios y calcular éste.
7. Se pretende invertir en dos productos financieros A y B. La inversión en B ha de ser al menos de 3000 € y no se quiere invertir en A más del doble de B. Se supone que A proporcionará un beneficio del 10% y B del 5%. Si se dispone de 12000 €, calcular de forma razonada cuánto se debe invertir en cada producto para maximizar el beneficio y determinar éste.
8. Una empresa dispone de un máximo de 16000 unidades de un producto que puede vender en unidades sueltas o en lotes de cuatro unidades. Para empaquetar un lote de cuatro unidades se necesita el triple de material que para empaquetar una unidad suelta. Si se dispone de material para empaquetar 15000 unidades sueltas, y si el beneficio que se obtiene por la venta de cada unidad suelta es de 2 € y de cada lote de cuatro unidades es de 7 €, calcular de forma razonada el número de unidades sueltas y de lotes de cuatro unidades que hay que preparar para maximizar el beneficio y calcular éste.
9. Si el conjunto factible (de un problema de p. l.) viene dado por las inecuaciones:
2x + y < 6
x + 2y < 4
x > 0
y > 0
y la función objetivo es f(x, y) = 2x + 4y ¿ Puede tener el problema solución única ?. Razona la respuesta. Comprueba tu afirmación resolviendo el problema por el método gráfico.
*10. Una empresa recibe el encargo de distribuir dos productos diferentes, A y B. La empresa cobra150ptas. por cada unidad del producto A que llega a su destino y 100ptas. por cada una del, el número de unidades repartidas del producto A no debe superar a la mitad del número de unidades repartidas del producto B y el total no puede ser superior a 250 unidades.
a) Hallar la función lineal que debe ser optimizada para obtener un beneficio máximo.
b) Hallar las restricciones y representar gráficamente el conjunto factible.
producto B, pero debe distribuir, al menos, 50 unidades del producto A y, al menos 100 del producto B. Además c) ¿Qué cantidades serán repartidas para maximizar el beneficio?.
d) Teniendo en cuenta que las soluciones deben ser enteras, elige un punto del conjunto factible representado por un par de números enteros y de forma que el beneficio no sea inferior a 29000ptas.
EJERCICIOS REPASO DE ÁLGEBRA
1. Dados los puntos A(2, -3), B(0, 1) y C(4, 0) hallar:
a) ecuación de la recta r que pasa por A y B en todas las formas que conozcas.
b) ecuación implícita de la recta s que pasa por B y C.
c) intersección de r y s
d) ecuación de la recta paralela a r que pase por C
2. Discute y resuelve el sistema, en los casos posibles:
a)
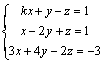
b)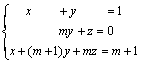
3. Un comerciante desea comprar dos tipos de frigoríficos, F1 y F2. Los del tipo F1 cuestan 300 € euros y los del tipo F2, 500 €. Sólo dispones de sitio para 20 frigoríficos y de 7000 € para hacer las compras. ¿Cuántos frigoríficos de cada tipo debe comprar para obtener beneficios máximos con su venta posterior, sabiendo que en cada frigorífico gana el 30% del precio de compra?
4. En la fabricación de piensos se utilizan tres ingredientes, P, Q y R. Se dispone de 90 toneladas de P, 90 de Q y 70 de R, y se desea fabricar dos piensos M1 y M2. Una tonelada de pienso M1 requiere 2 toneladas de P, 1 de Q y 1 de R y se vende a 12 €; y una tonelada de M2 requiere 1 tonelada de P , 2 de Q y 1 de R, y se vende a 10 €. ¿Cuántas toneladas de cada pienso deben facturarse para obtener el mayor beneficio?
Otras páginas:
Cuaderno para 2º Bach Matemáticas en el Bachillerato
 (según tengan una ó infinitas soluciones)
(según tengan una ó infinitas soluciones)