S I S T E M A S   L I N E A L E S

 

SI QUIERES PUEDES DESCARGARTE EL ARCHIVO ZIP, TAMBIÉN ESTÁ EN FORMATO pdf (la mejor forma de verlo)

 

INTRODUCCIÓN

Muchos problemas que se nos plantean pueden reducirse a encontrar uno o varios números desconocidos, que llamamos incógnitas, sujetos a una serie de condiciones que nos permiten plantear una o varias ecuaciones (sistemas). El objetivo de este tema es el  estudio de los sistemas lineales y de métodos para su resolución^[1]. Terminaremos el tema dando algunas estrategias para el planteamiento de los llamados problemas lineales y algunos “modelos” resueltos.

1. Igualdades, identidades, ecuaciones (repaso^[2]).

Una igualdad, (=), es una relación de equivalencia^[3] entre dos expresiones, numéricas o literales, que se cumple para algún, alguno o todos los valores. Cada una de las expresiones recibe el nombre de miembro.

 

 

 

 

 

 

 

· Si la igualdad se cumple entre números se denomina identidad numérica.

Ejemplo 1: 2 +4  +5 = 1 +10

· Una identidad literal es una igualdad que se cumple para todos los valores.

Ejemplo 2: 

· Cuando la igualdad se convierte en identidad numérica sólo para determinados valores se la llama ecuación. A las letras se les llama indeterminadas o incógnitas.

Nota : El segundo miembro de la ecuación se puede considerar siempre que es 0.

Ejemplo 3:  5x - 1 = 2x -3  es una ecuación con una incógnita.;  se puede escribir 3x + 2 = 0, trasponiendo términos.

Al valor, o valores, que convierten la ecuación en identidad numérica se les llama solución (o raíz) de la misma.

Ejemplo 4. Una solución de la ecuación del ejemplo 3 es x=-2/3 .

Ejercicio 1. Encuentra 2 soluciones de la ecuación 3x-2y-1=0

Resolver una ecuación es encontrar todas sus soluciones o llegar a la conclusión de que no tiene ninguna.

Ejemplo 5.

a) x² + 1=0 es una ecuación sin soluciones en R.

 b) 2x +3y = 0 tiene infinitas soluciones, (0,0), (-3,2), (3, -2)....

2. Ecuaciones lineales.

Si las expresiones de los miembros de las igualdades son polinomios se las llama ecuaciones polinómicas.

Cuando son polinomios de grado uno se trata de las ecuaciones lineales.

Ejemplo 6.   5x - 6y - 1 = 0, es una ecuación lineal con dos incógnitas.

En general una ecuación lineal con n incógnitas será de la forma:

A los a_i se les llama coeficientes de las incógnitas y a b término independiente

Para encontrar una solución particular de una ecuación lineal con n incógnitas, se les da valores arbitrarios a n - 1 cualesquiera de ellas, con lo que se reduce la ecuación a otra de una sola incógnita y se resuelve.

Ejemplo 7. Vamos a encontrar dos soluciones particulares de la ecuación 3x +2y -z = 1.

Si damos a x el valor 0 y a y el valor 1, se obtiene  z= 1Þ la solución es ( 0, 1, 1).

Análogamente,  x = 1, y = 0 , nos da z = 2 y la solución es la terna (1,0,2). Comprobarlas.

Para encontrar la solución general, de la ecuación lineal, se consideran a n - 1 incógnitas como parámetros y se resuelve en función de éstos.

Al número de parámetros de una ecuación lineal se le denomina grado de libertad o de indeterminación de la misma.

Ejemplo 8.

Consideremos la ecuación  2x - 3y + z = 1; es una ecuación lineal con tres incógnitas;  3 -1 = 2, es decir depende  2 parámetros. La ecuación tiene por lo tanto dos grados de libertad.

Si hacemos  x = t, e y = s, quedaría z = 1 - 2t + 3s.

La solución sería ( t,  s, 1 -2t + 3s).

3. Sistemas de ecuaciones lineales. Clasificación.

Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales.

Ejemplo 9:  es un sistema de 2 ecuaciones con dos incógnitas.

Un sistema de m con n incógnitas se puede escribir, en general:

(1)

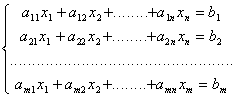
En este sistema x₁, x₂, ....x_n  son la incógnitas; los números a_ij son los coeficientes del sistema y b₁, b₂,......b_m los términos independientes.

El sistema se dirá homogéneo si todos los b_j son cero.

Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.

Nota. Los sistemas homogéneos tienen siempre, al menos, una solución la (0,0,..0) que se llama solución trivial.

Clasificación de sistemas.

Si el sistema tiene solución se dice compatible. Si la solución es única se dice determinado y en otro caso indeterminado. Si no tiene solución se dirá incompatible.

Es decir se clasifican, según el número de soluciones en:

 

 

Ejemplo 10. El sistema:

 es incompatible.

 

4. Método de Gauss para la resolución de sistemas lineales. Tratamiento matricial.

Definición 1. Dos sistemas de ecuaciones lineales son equivalentes si tienen el mismo conjunto de soluciones.

El método general de resolver sistemas de ecuaciones es encontrar otro sistema equivalente de más fácil resolución^[4].

Definición 2.  Se llaman transformaciones elementales (o de equivalencia) a aquellas modificaciones de un sistema lineal que lo transforman en otro equivalente.

Proposición. Las siguientes transformaciones son elementales.

1) Permutar dos ecuaciones.

2) Multiplicar una ecuación del sistema por un número distinto de 0.

3) Sumar a una ecuación del sistema otra multiplicada por un número.

4) Cambiar el orden de las incógnitas.

5) Despejar una incógnita en una ecuación y sustituirla en las demás ecuaciones.

6) Suprimir o añadir una ecuación que sea combinación lineal de las otras.

La demostración es inmediata en todos los casos.

Método de Gauss

El método de Gauss para la resolución de sistemas lineales se puede considerar como un generalización del de reducción (para los sistemas con dos o tres incógnitas). En esencia consiste  en hacer, al sistema de ecuaciones lineales, determinadas transformaciones elementales a fin de obtener un sistema escalonado, más fácil de resolver.

Lo explicaremos utilizando un ejemplo:

Ejemplo 11. Consideremos el sistema :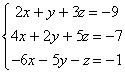

En primer lugar cambiamos el orden de las incógnitas x e y  (pues el coeficiente de y es 1, y nos servirá de “pivote”), el sistema queda: 

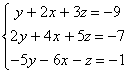
Multiplicamos la 1ª ecuación por 2 y se la restamos a la segunda:

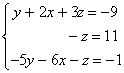
Permutamos las ecuaciones 2ª y 3ª:

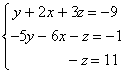
Multiplicamos la 1ª ecuación por 5 y se la sumamos a la 2ª:

 

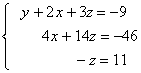
que es un sistema escalonado.

Hasta aquí es el método de Gauss, ya se ha conseguido un sistema escalonado ahora para resolverlo se procede:

z=-11, de donde 

4x = -46-14(-11)Þ x=54/2, la y la obtenemos sustituyendo estos dos valores en la ecuación 1ª ;

 y =-9-54+33, y=-30.

La solución es:        (54/2,-30,-11)

El método se puede generalizar al caso de m ecuaciones con n incógnita, y se puede llegar a enunciar el siguiente:

Teorema . Todo sistema de m ecuaciones con n incógnitas, puede reducirse a un sistema equivalente del tipo:

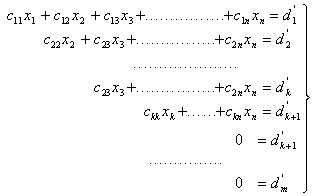
 (Se harían cero los coeficientes necesarios hasta dejarlo escalonado usando el método de Gauss que se ha indicado en el ejemplo)

Consecuencias:

 1) Si alguno de los d_k+1, .....,d_m, es distinto de 0 el sistema es incompatible.

2) Si todos los d_k+1, .....,d_m son 0 es compatible, y a su vez se pueden presentar dos casos:

\ Si k = n el sistema queda reducido a uno equivalente con el mismo número de ecuaciones que de incógnitas. Luego la solución es única: compatible determinado^[5].

 

\ Si k<n, es decir, hay más incógnitas que ecuaciones, entonces, asignando valores arbitrarios a las incógnitas x_k+1, .....,x_n,  existirá una solución única de las x_1,, x₂,....,x_k, y  por lo tanto el sistema tiene infinitas soluciones; es indeterminado con n - k grados de libertad.

 

(El teorema nos da una forma de clasificar el sistema).

Ejemplo 12.  Resolver el sistema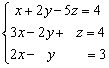

Solución:  Multiplicamos a la 1ª ecuación por 3 y se la restamos a la 2ª, queda:

   

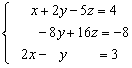
Multiplicamos la 1ª por 2 y se la restamos a la 3ª é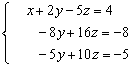

Dividimos por -8 la 2ª ecuación: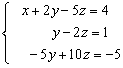

Multiplicamos la 2ª ecuación por 5 y se la sumamos a la 3ª, nos queda:

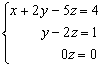                                    ,  la 3ª ecuación puede eliminarse,

El sistema nos queda de dos ecuaciones con tres incógnitas, (compatible indeterminado con un grado de libertad)

Pasando la z al otro miembro y haciendo z = t, ,

De donde: x = 4 - 2(1 + 2t) + 5t = 2 + t;   la solución sería:

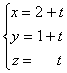
Observación: En todo el proceso lo que se manejan son los coeficientes de las incógnita y los términos independientes.

Teniendo en cuenta la observación anterior abreviaremos el proceso escribiendo sólo los coeficientes de las incógnitas y los términos independientes, entre paréntesis y separados por una barra, esto se denomina tratamiento matricial^[6] del sistema.

 

En el ejemplo siguiente se muestra el esquema de trabajo que se sigue.

Ejemplo 13. Resuelve el sistema :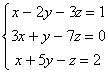

Solución.

Considerando la disposición indicada^[7]: 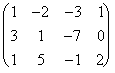 ^{F2 -3F1  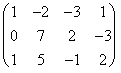    F3 - F1}

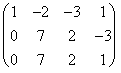F₃ -F₂  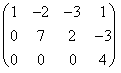           , luego el sistema es incompatible.

(Observar que se ahorra bastante tiempo con la forma matricial del método de Gauss.)

Nota: Cuando permutemos las incógnitas se debe indicar. Se suelen escribir las incógnitas encima de la  matriz ampliada del sistema.

Ejercicio 2. Resuelve el ejemplo  11 usando la forma matricial.

Aplicación del método de Gauss a la discusión de sistemas

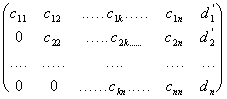
Las consecuencias del teorema anterior se pueden expresar  con la nueva  notación así:

1)  Si la disposición final de los coeficientes al aplicar el método de Gauss es:

, el sistema es incompatible.

2)   Se pueden presentar dos casos:

 , el sistema es compatible determinado

, compatible indeterminado

Ejercicio  3. Clasificar los siguientes sistemas y si fuese posible resolverlos:

a) 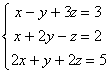;  b);  c)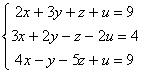

Ejercicio 4.  Calcula el valor de m para que el sistema sea compatible determinado.

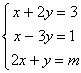
5. Eliminación de parámetros.

Hemos visto que las soluciones de un sistema en algunos casos dependen de uno ó  varios parámetros. El método de Gauss, además de resolver sistemas de ecuaciones lineales, permite apoyándose en la compatibilidad de éstos, eliminar los parámetros y obtener el sistema que genera dicha solución.

Ejemplo 14.  Eliminar t y s en el sistema:

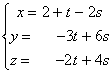
Solución

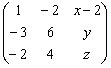^F2+3F1  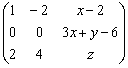      F₃ - 2F₁     .

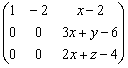Como el sistema es compatible se deduce que:

   ,  que es el  sistema buscado.

Ejercicio 5. Eliminar los parámetros t y s en el siguiente sistema:

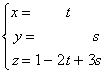
6. Resolución de sistemas dependientes de un parámetro.

Un sistema lineal es dependiente de un parámetro cuando uno (o varios) de sus coeficientes (o términos independientes) es variable. Para su resolución^[8] aplicamos de nuevo el método de Gauss, discutiendo las soluciones según los valores del parámetro (coeficiente variable).

 

Ejemplo 15. Discutir el sistema según los distintos valores del parámetro k:

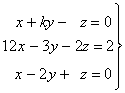
Cambiamos, en primer lugar, el orden de las ecuaciones y de las incógnitas y nos queda el sistema equivalente:                                                                                                         x       z       y        

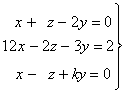, la matriz ampliada del sistema es: 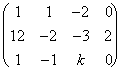^{F2 - 12F1}

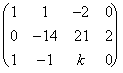^{F3 - F1  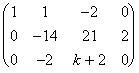         F2 / (-7)  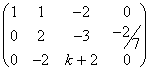F3+F2}

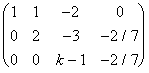              ^{Luego nos queda:}

 

Discusión 

a)  Si k =1,  nos quedaría  0.y =-2/7, con lo que el sistema sería incompatible

b)  Si k ¹1 , y se puede despejar con lo que el sistema es compatible determinado.

Ejercicio 6.  Discute y resuelve el sistema anterior en el caso de que fuese homogéneo.

Ejercicio 7. Clasifica  y resuelve, según los distintos valores del parámetro  k , el sistema:

  

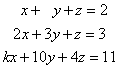
Ejercicio 8. Hallar los valores de m para los cuales el sistema :

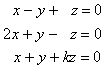
tenga soluciones distintas de la trivial. Hallar en ese caso la solución general.

7. Significado geométrico de las ecuaciones y sistema lineales^[9].

 

I) Significado geométrico de las ecuaciones lineales

Las soluciones de las ecuaciones lineales de 2 y 3 incógnitas pueden interpretarse de un modo geométrico en el plano y en espacio tridimensional, respectivamente.

1) La ecuación ax + by +c = 0, como se ha visto en cursos anteriores, representa una recta en el plano afín.

 En efecto:  si hacemos x = t, quedaría , que podemos escribir:

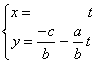
“Son las ecuaciones paramétricas  de la recta que pasa por el punto (0,-c/b) y  (1,-a/b) es un vector de dirección.”

Ejemplo 16.  Las ecuaciones paramétricas de la recta  6x - 2y + 5 = 0, son:

, pasa por el punto (0,5/2), y  u n vector de dirección es  (1,3) .

2) En el espacio tridimensional real la ecuación :

 ax + by + cz + d = 0, representa un plano.

En efecto, como, para determinar un plano hay que conocer:

1) un punto por el que pase

2) dos vectores de dirección (vectores l.d. contenidos en el plano)

Si hacemos x = t, y = s, nos quedaría: ,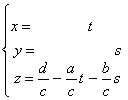

 

Son las llamadas ecuaciones paramétricas del plano que pasa por (0,0,d/c) y tiene por vectores de dirección a (-b/a,1,0) y a  (-c/b,0,1).

Podemos pues concluir que toda ecuación lineal de tres incógnitas representa un plano.

 

Ejemplo 17. Vamos a encontrar las ecuaciones paramétricas del plano, solución de la ecuación lineal,

2x - 3y + z =1. Solución:

Como ya hemos visto^[10] esta ecuación se puede escribir:,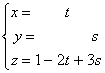

que son las ecuaciones del plano que pasa por el punto  P(0,0,1) y tiene como vectores de dirección a v(1,0,-2) y w(0,1,3).

Ejercicio 9. Hallar las ecuaciones paramétricas de los planos siguientes:

a) x = 2; b) 2x + z = 0; c) 2x-4y +2z -1 = 0

II) Significado geométrico de los sistemas.

Al igual que en las ecuaciones lineales, consideramos la interpretación geométrica en el plano (sistemas de ecuaciones con dos incógnitas) y en espacio (sistemas de ecuaciones con tres incógnitas)

♦ Sistemas de ecuaciones lineales con dos incógnitas.

Posiciones relativas de rectas en el plano.

Se propone como ejercicio 10. para el alumno.

♦ Sistemas de ecuaciones lineales con tres incógnitas.

A) Sistemas de 2 ecuaciones con 3 incógnitas.

La resolución del sistema:   

en términos geométricos es el estudio de las posiciones relativas de dos planos, casos que se presentan:

■ Planos paralelos.  Sin puntos comunes, cuando el sistema sea incompatible.

●  Planos que se cortan en una recta. Si el  sistema es compatible pero indeterminado, con un grado de libertad.

■  Planos coincidentes. Ocurre este caso cuando las dos ecuaciones son equivalentes y el sistema es compatible indeterminado con dos grados de libertad

B) Sistemas de tres ecuaciones con tres incógnitas:

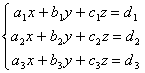
Cada ecuación representa un plano en el espacio tridimensional. Luego se trata de estudiar la posición relativa de tres planos en el espacio. Las soluciones del sistema son geométricamente los puntos de intersección de los tres planos, los casos son:

▲ Un punto único.  Sistema  compatible determinado.. Los tres planos se cortan en P.

 

 

 

 

 

 

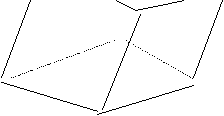 P         

· Una recta. Son soluciones todos los puntos representativos de la recta común. Sistema compatible indeterminado con un grado de libertad.

 

Los planos se cortan en r.

 

 

                                                         r

 

 

 

 

 

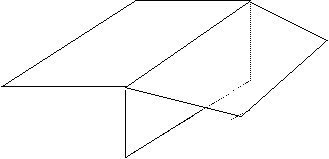
▼ Un plano. Los planos son coincidentes. El sistema es compatible indeterminado con dos grados de libertad.

◄ Ningún punto. El sistema es incompatible. Esta situación se presenta geométricamente de distintas maneras. Para estudiar las posiciones relativas de los planos hay que tomarlos de dos en dos.

Se pueden presentar varios casos: Que los planos sean paralelos:

 

 

 

 

 

 

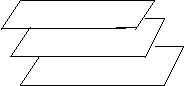Ejercicio 11 . Estudiar los demás casos (hay otros tres).

Ejercicio 12. Interpreta geométricamente las soluciones del ejercicio 3. apartados a) y b).

 

8. Estrategias para la resolución de problemas lineales.

 

Para resolver un problema se necesita realizar cuatro fases^[11]:

 

1ª. Comprender el problema.

Hay que leer el problema hasta familiarizarse con él y que podamos contestar, sin dudar, a las siguientes preguntas:

¿Cuáles son los datos? ¿cuáles son las incógnitas? ¿son las condiciones suficientes para determinar a las incógnitas? ¿son  insuficientes? ¿son redundantes?....

 

2ª Concebir un plan.

Determinar la relación entre los datos y las incógnitas.

De no encontrarse una relación inmediata puedes considerar problemas auxiliares.

¿Conoces problemas relacionados con éste?

¿Podrías plantear el problema de forma diferente?

¿Puedes cambiar la incógnita o los datos o ambos si fuera necesario, de tal forma que la nueva incógnita y datos estén en una relación más sencilla?...

¿Has considerado todas las nociones esenciales del problema?

.................

Obtener finalmente un plan de solución.

Para nuestro caso:

Escribir las ecuaciones que relacionan datos e incógnitas y analizar el sistema que forman.

 

3ª. Ejecutar el plan.

Resuelve el sistema por los métodos estudiados.

 

4ª. Examinar la solución obtenida.

Comprobar si las soluciones obtenidas son válidas y proceder en consecuencia.

 

Problemas resueltos

1. Alejandra tiene 27 años más que su hija Carmen. Dentro de 8 años, la edad de Alejandra doblará a la de Carmen. ¿Cuántos años tiene cada una?

Solución

1º. Comprender el problema.

Es un problema con dos incógnitas y dos condiciones, luego suficientes para poder determinarlas. Llamamos x a la edad de Alejandra e y a la de su hija.

Ordenamos los elementos del problema:

 

	Hoy	dentro de 8 años
La madre	x	x + 8
La hija	y	y + 8

 

2º. Concebir un plan.

Escribimos las ecuaciones que relacionan los datos con las incógnitas:

     x = 27 + y       

x + 8 = 2(y+8)

Es un sistema lineal de dos ecuaciones con dos incógnitas.  Lo resolveremos por el método de sustitución.

3º Ejecutar el plan.

            x = 27 + y       

Entonces:

           27 + y +8 = 2(y+8) de donde  35 -16 = y Þ y = 19, x = 46

4º Examinar la solución obtenida .

La solución obtenida es factible por ser entera. El método empleado se puede usar en problemas “similares”.

Nota. En los demás problemas  el alumno indicará las cuatro fases.

2. Un grupo de personas se reúne para ir de excursión, juntándose un total de 20 entre hombres, mujeres y niños. Contando hombres y mujeres juntos, su número resulta ser el triple del número de niños. Además, si hubiera acudido una mujer más, su número igualaría al de los hombres. ¿Cuántos hombres, mujeres y niños han ido de excursión.

Solución

Sean:

hombres	x
mujeres	y
niños	z

Luego:

x + y + z = 20 

x + y  = 3z                     Es un sistema de tres ecuaciones con tres incógnitas.

x  = y + 1

Se resuelve por el método de Gauss.

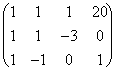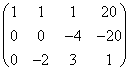Þ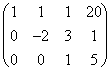ÞÞ

El sistema que resulta es:

x +   y +   z = 20 

    -2 y + 3z =  1                   

                z =  5

 Es un sistema de tres ecuaciones con tres incógnitas y por tanto c.d

Comprobar que la solución es:   z = 5, y = 7 y x= 8.

3. Lewis Carroll, autor de Alicia en el país de las maravillas propone un problema que puede enunciarse así: el consumo en una cafetería de un vaso de limonada, tres sandwiches y siete bizcochos ha costado 1 chelín y 2 peniques, mientras que un vaso de limonada, cuatro sandwiches y diez bizcochos vale 1 chelín y 5 peniques. Hallar cuál es el precio:

1º) De un vaso de limonada, un sandwich y un bizcocho.

2º) De dos vasos de limonada, tres sandwiches y cinco bizcochos.

Resolver el problema recordando que 1 chelín vale 12 peniques.

Solución

Es un problema con tres incógnitas y sólo dos condiciones, luego los valores de las incógnitas no se podrán determinar.

Llamamos : x al precio de un vaso de limonada

y al precio de un sandwich

z  al precio de un bizcocho

Entonces:  x + 3y +   7z = 14  (peniques)

x + 4y + 10z = 17

Lo resolvemos por Gauss:

Þ

el sistema escalonado es:

                x + 3y + 7z = 14  (peniques)   

                        y + 3z =  3,    que tiene menos ecuaciones que incógnitas.  Es por tanto un sistema compatible indeterminado, con  un grado de libertad

Haciendo z=t, nos queda

x = 5 + 2t

y =  3 - 3t

z =         t

Encontremos los precios de las combinaciones que nos piden.

1º) x + y + z = (5 + 2t) + (3 - 3t) + t =8 peniques. (no depende de t)

2º) 2x + 3y + 5z = 10 + 4t + 9 -9t +5t= 19 peniques.     “

 

4. Cierto día me dijo un amigo. Mi edad es el doble de la que tú tenías cuando yo tenía la edad que tú tienes; además cuando tú tengas la edad que yo tengo, nuestras edades sumarán 63. ¿Se pueden hallar las edades con esos datos?. Hállalas.

Solución

Sean x, y  las edades de mi amigo y la mía; t el nº de años que hace que tenía  yo su edad y s el nº de años que falta para que él tenga la mía.

 

	Hoy	Tenía tu edad	Tengas mi edad
Amigo	x	x - t	x + s
Yo	y	y-t	y + s

 

Las ecuaciones que relacionan los datos con las incógnitas son:

x = 2(y - t);   x - t = y;  y + s = x;     x + s + y +s =63

Forman un sistema de 4 ecuaciones con cuatro incógnitas:

x - 2y + 2t     = 0

x -  y  -   t      = 0  

x -   y        - s = 0

x +  y + t + s = 63

Resolviendo por Gauss:

 ÞÞÞ

Þ s = 7, t = 7, y = 21, x = 28. (Comprobarlo)

 

Nota. El problema también se podría haber resuelto usando sólo dos incógnitas. Comprobarlo.

 

5. Compré 100 tornillos de distintas medidas por un total de 500 ptas. Los precios por unidad fueron: 50 ptas. los de medida A, 10 ptas. los de medida B y 1 ptas.  los de medida C. ¿Cuántos tornillos compré de cada clase? .Sol 1 de A, 39 de B y 60 de C.

Solución

 Sean: x , y,  z el nº de tornillos de medidas A, B y C respectivamente. Se verifica:

    x +   y + z = 100   

50x +10y +z = 500

Se resuelve por Gauss ÞÞ Luego queda :

z     +    y +     x = 100

           9y + 49x = 400  que tiene menos ecuaciones que incógnitas y por lo tanto es indeterminado con un grado de libertad.  Haciendo x= t, nos queda

x =      t

y =

z= 100 - - 9t = 100 -40t

Como las soluciones tienen que ser enteros positivos se sigue que t tiene que ser menor que 3 (para que z de positivo),  luego debe de valer 1 ó 2.

La solución válida es t=1, pues,  para t=2 y  da decimal.

Por lo tanto : x =1, y== 39, z= 60.

Y la solución es 1 de A, 39 de B y 60 de C.

 

Actividades

 

1. Resuelve e interpreta geométricamente.

a)   x +  y +  z =   0           b) 2x + 5y       = 16      c)  x + 2y =3

    7x  - 4y  -  z = -11               x + 3y -2z =-2           3x +  y = 4

    4x + 6y + 8z =   2                x +         z = 4           2x -  y = 1

d)    x +  y +  z = 6           e) 2x -  y + z = 3      f)  x -   y +  z = 0

               y  -  z = 1                x - 2y -z = 3          3x + 2y - 2z = 1

       x + 2y        = 0              4x - 5y -z = 9           5x               = 1

 

2. Calcula k para que los planos siguientes se corten en una recta.

  x +    y  +   z = 2

2x +  3y  +   z = 3

k x + 10y + 4z =11

 

3.  Discutir el siguiente sistema según los valores del parámetro.

  x +        y + k z = 1

k x + (k-1)y +   z = k

  x +        y +   z = k + 1

 

4.  a)Hállense todos los valore posibles de a, b, y c para que los planos siguientes sean paralelos o coincidentes:

            x + by + 5cz =1       

2x + (a-1)y + (3b-1)z =2

b) ¿Para qué valores específicos de a, b y c los dos planos anteriores son coincidentes y pasan por el punto (1,2,-1)

 

5. Un problema de grifos te conduce a un sistema del tipo:

a/x +  a/y  = m

b/x  - b/y  = m²    ;       donde a, b y m son constantes no nulas y  2ab = b +a m

Si intentas resolver dicho sistema, ¿qué valores de a te conducen a un sistema incompatible?

Sol. a =1.

 

6. Entre tú y yo tenemos 12 600ptas. Si lo que yo tengo aumentara en un 14%, entonces tendría el 75% de lo que tienes tú. ¿Cuánto tenemos cada uno?

 Sol. Yo tengo 5 000 y tú 7 600.

 

7. Un grifo A tarda en llenar un depósito el doble de tiempo que otro grifo B. Abiertos simultáneamente, llenan el depósito en dos horas?. ¿Cuánto tarda cada uno por separado?

 Sol. A tarda 6 horas y B tarda 3.

 

8. Queremos averiguar las edades de una familia formada por los padres y los dos hijos. Si sumamos sus edades de tres en tres obtenemos 100, 73, 74 y 98 años respectivamente. ¿Cuál es la edad de cada uno de ellos?.

 Sol. Padre 42, madre 41, hijos 17 y 15.

 

9. Nos hemos gastado 4260ptas. por una botella de ginebra, una de ron y dos de licor de manzana, pero, por tres de ginebra, cuatro de ron y una de licor de manzana hubiésemos pagado 7380ptas. y por dos de ginebra y tres de ron pagaríamos 4350. ¿Cuánto vale una botella de licor de manzana?.

Sol 1230ptas.

 

10. Los lados de un triángulo ABC miden 2, 3 y 4 m, respectivamente. Hállense lo lado de otro triángulo A’B’C’ que es semejante al anterior y tiene 36m de perímetro. Sol. 8, 12 y 16.

 

11. La suma de las tres cifras de un nº es 12, la diferencia entre este número y el que resulta al invertir el orden de sus cifras es 198 y la cifra de las decenas es la media aritmética de las otras dos cifras. Halla el número pedido.

 Sol. El nº es el 543.

 

12. En un garaje hay 100 vehículos entre motos, triciclos y coches. Para combatir el insomnio, el vigilante ha decidido entretenerse contando las ruedas y pensando luego cuántos vehículos de cada clase podría haber. Si ha contado un total de 328 ruedas,:

a) Entre qué valores puede estar el nº de coches?.

b) ¿Es posible que haya sólo un triciclo? ¿Por qué?

c) Si hubiera 2 triciclos por cada 5 motos, ¿Cuántos vehículos habría de cada clase?

Sol.  a) entre 29 y 63;

        b) No, porque saldría decimal el nº de motos;

        c) 58 coches, 12 triciclos y 30 motos.

 

13. Tres máquinas limpiadoras A, B y C trabajando juntas realizan la limpieza de unos grandes almacenes en 4 horas. Si se estropea la máquina B, entonces a y C realizan el trabajo en 6 horas,  pero si se estropea la máquina C entonces A y B lo realizan en 8 horas. ¿Cuánto tardaría cada máquina por separado en realizar el trabajo?.

 Sol. A, 24 horas; B, 12 horas y C  8 horas.

 

14. Un tren transporta 500 viajeros y la recaudación del importe de sus billetes asciende a 352500ptas. Calcular cuántos viajeros han pagado el importe total del billete, que vale 1500ptas., cuántos han pagado el 20% del billete y cuántos el 50%, sabiendo que el número de viajeros que han pagado el 20% es el doble del número de viajeros que pagan el billete entero.

 Sol. 150, 300 y 50.

 

15. Tres amigos acuerdan jugar tres partidas de dados de forma que, cuando uno pierda una partida, entregará a cada uno de los otros dos una cantidad igual a la que cada uno de ellos posea en ese momento. Cada uno perdió una partida y al final cada uno tenía 24euros. ¿Cuánto tenia cada jugador al comenzar el juego?.

Sol. 39, 21, 12.

 

 

Soluciones de los problemas propuestos en las actividades.

4.  a)  Por la condición de paralelismo:

1/2 = b/(a-1) = 5c/(3b - 1) = 1/2; serán coincidentes.

Se tiene:

         1/2 = b/(a-1), de donde a - 1 = 2b Þ a - 2b   - 1 =0

         1/2 = 5c/(3b - 1) Þ 3b - 1 = 10c  Þ   3b - 10c -1 =0

El sistema es indeterminado, si hacemos b = t, nos queda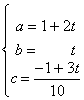      [1]

b)  Si  queremos que además pasen por (1, 2, -1) se tendrá:

                   1 + 2t -  (-1 +3t)/2 = 1, de donde t = -1,

Sustituyendo en [1] se obtiene: a = -1, b = -1, c = -2/5.

5. 1/x + 1/y  = m/a   (a¹0)

    1/x  - 1/y  = m²/b   (b¹0)               Sumando:    

 2/x = m/a + m²/b= (mb + am²)/ab,  como por hipótesis 2ab = b + am, entonces 1/x = mÞx = 1/m;  sustituyendo en la 1ª ecuación:

1/y = m/a - m =m(1 - a)/aÞ y = a/m(1 - a), luego si a =1 el sistema sería incompatible.

(comprobar que si a¹1, entonces b ¹ m)

6. Sea x el dinero que tengo yo e y el que tienes tú.

Lo mío aumenta un 14%, luego tendré: x + 0,14x = 1,14x

Entonces:

x +y = 12 600

1,14x = 0,75y   de donde x = 5 000ptas. e y = 7 600ptas. (comprobarlo)

7.  Los problemas de llenado y vaciado se resuelven operando con las fracciones de depósito que llena cada grifo en una hora.

Si el grifo A tarda x horas en llenar el depósito, en 1 hora llena 1/x de depósito.

          “     B      “  y       “                   “                   1 hora      “     1/y       “

A  + B      tardan   2h            “                 “              1 hora      “      1/2      “

Las condiciones nos permiten plantear dos ecuaciones:

1/x  +   1/y  = 1/2

                x = 2y,      sustituyendo en la 1ª ecuación obtenemos y =3, x =6

 

8.  Llamando x, y, z y u a las edades del padre, la madres y los dos hijos respectivamente. Se tiene:

x + y + z       = 100

      y + z + u = 73

x +       z + u = 74

x + y        + u = 98

 es la matriz ampliada del sistema.

Comprobar que aplicando el método de Gauss se llega al sistema:

 

 

x + y + z       = 100

      y + z + u = 73

           z + 2u = 47

                  3u = 45

 de donde u =15, z =17, y = 41, x =42.

9. Si llamamos x, y, z a los precios de las botellas de ginebra, ron y licor de manzana respectivamente se tiene:

  x +   y + 2z = 4260

3x + 4y +   z = 7380

2x  + 3y         = 4350

Resolviendo el sistema se obtiene z =1230.

10.  Sean x, y , z los lados, entonces 

(1)        x + y + z =36

al  ser  los triángulos semejantes los lados son proporcionales, por lo tanto:

==  =  = 4     por (1),

de donde x =8,   y =12,   z =16.

Nota.  Se ha usado para resolver este problema una propiedad de la proporcionalidad directa, pero también podría haberse resulto planteando el sistema de tres ecuaciones que proporcionan las condiciones. Hacerlo.

11.  Sea    x y z el número que buscamos, las condiciones nos permiten plantear 3 ecuaciones:

                               

 

                                     x + y + z =12

100x + 10y +z - (100z + 10y + x ) =198

                                                  y =

de donde:              x + y + z =12

                 x       - z  =2

                 x - 2y +z =0 ,

 que resuelto da  z = 3, y = 4 ,x = 5 y el nº pedido el 543.

12.

	Vehículos	Ruedas
Motos	x	2x
Triciclos	y	3y
Coches	z	4z
Total	100	328

Utilizando las condiciones podemos encontrar:

    x +   y +  z = 100

   2x + 3y + 4z = 328 ,  resolvemos por Gauss:

ÞÞ

x + y +  z  = 100

      y + 2z = 128       

sistema que tiene menos ecuaciones que incógnitas, luego es indeterminado y con un grado de libertad.

Haciendo z = t, nos quedaría:

y = 128 - 2t,  x = 100 - (128 - 2t) -t = -28 + t, es decir las solución es:

a) Para determinar  qué valores puede tomar z, número de coches , imponemos que los de y, x sean enteros positivos, Þ,  t>28   y  t<64. Luego z está entre 29 y 63.

b) Si y =1, obtendríamos t = 27/2 =z que no es válida como solución  por ser decimal.

c)Al sistema anterior añadimos la ecuación que nos da la condición de 2 triciclos por cada 5 motos, es decir  2x - 5y = 0, con lo que tendremos tres ecuaciones con tres incógnitas:

x +    y  +  z = 100

2x + 3y + 4z = 328

2x  - 5y         =   0

Utilizamos el método de Gauss:

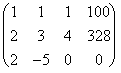ÞÞ

Es sistema que resulta es:  x + y +   z = 100

                                               y + 2z = 128 

                                                   12z = 696

de donde 12z = 696Þ z = 58, sustituyendo este valor en la 2ª ecuación da y =12, y llevando esos dos valores a la 1ª x =30..

13.  Es un problema tipo “grifos”

 

	Tiempo limpieza	Limpieza en 1 hora
A, B y C juntas	4	1/4
A y C	6	1/6
A y B	8	1/8

 

Llamamos x, y, z   al nº de horas que tarda cada máquina por separado en hacer todo el trabajo.

Entonces en 1 hora A limpiará 1/x del total

                   1 hora B    “          1/y      “

                   1 hora C     “          1/z      “

Por comodidad hacemos un cambio de variables,  X = 1/x, Y = 1/y , Z =1/z.

Entonces : X + Y + Z =1/4

                 X +        Z = 1/6

                 X +  Z        = 1/8

Resolviendo por Gauss se llega a que :

X =1/24, Þ x =24; Y =1/12 Þ y =12; Z =1/8 Þ z =8.

 

14.. Sean x, y, z el nº de pasajeros que pagan el 100 %, el 20% y el 50% del billete respectivamente.

nº de viajeros	precio pagado
x	1500
y	300
z	750

 

Entonces:                 x  +  y + z = 500

                1500x + 300y + 750y = 352.500 ,  30x +6y +15z = 7050

                                               y = 2x

De donde:    3x + z = 500  

                42x +15z = 7040   

Por reducción  3x= 450, luego : x =150,  y =300, z =50.

Comprobar el resultado utilizando Gauss.

15. Sean A, B y C los tres amigos, x, y,  z el dinero que poseen al empezar la 1ª partida, respectivamente.

 

	A	B	C
D. al empezar	x	y	z
pierde A	x -y-z	2y	2z
pierde B	2(x-y-z)	2y-(x-y-z)-2z	4z
pierde C	4(x-y-z)	2(2y-(x-y-z)-2z)	4z-2(x-y-z)-(2y-(x-y-z)-2z)
D. al terminar	24	24	24

 

 

Luego  4(x-y-z) = 24; 2(2y-(x-y-z)-2z) =24; 4z-2(x-y-z)-(2y-(x-y-z)-2z=24, de donde:

  x  -   y - z =  6

 -x + 3y - z = 12

              4z = 48 Þ z =12            ( se ha utilizado que x-y-z =6),

de donde se obtiene x =39, y =21. 

 

Problemas  propuestos en Selectividad LOGSE^[12]

 

1.  En una reunión hay 40 personas. La suma del número de hombres y mujeres triplica el número de niños. El número de mujeres excede en 6 a la suma del número de hombres mas el número de niños. Averiguar razonadamente cuántos hombres, mujeres y niños hay.

2. Hemos invertido 4000000 de pesetas en acciones de las empresas A, B y C. Después de un año, la empresa A va a repartir. un beneficio del 6%, la B del 8% y la C del 10%. En total recibimos 324826ptas.

a) Deduzca razonadamente si se puede averiguar  o no que invertimos en cada empresa.

b) Deduzca razonadamente que invertimos en cada empresa sabiendo que en la empresa C invertimos el doble que en la empresa A.

3. Un estudiante obtuvo un 6 en un examen de Matemáticas que constaba de tres preguntas. En la primera pregunta obtuvo una calificación igual al doble de la calificación que obtuvo en la segunda pregunta y en la tercera pregunta obtuvo una calificación igual a la suma de las calificaciones de las otras dos preguntas. Averiguar razonadamente la calificación de cada pregunta.

4. Un tren transporta 500 viajeros y la recaudación del importe de sus billetes asciende a 2115 euros. Calcular de forma razonada cuántos viajeros han pagado el importe total del billete, que vale 9 euros, cuántos han pagado el 20% del billete y cuántos el 50%, sabiendo que el número de viajeros que han pagado el 20% es el doble del número de viajeros que han pagado el billete entero.

 

 

Si quieres mas ejercicios visita este enlace EJERCICIOS MODELOS

 

Matemáticas en el Bachillerato                                                     Selectividad