INICIACIÓN A LA GEOMETRÍA ANALÍTICA PLANA
SI NECESITAS TEORÍA DE ESTE TEMA VISITA EL “RESÚMEN TEÓRICO”
1. a) Si dos vectores tiene la misma longitud, ¿podemos asegurar que son iguales? Razona la respuesta . Pon ejemplos
2. a)¿Cuántos sentidos pueden existir en una dirección dada?
b) ¿Es posible que dos vectores tengan la misma dirección, punto de aplicación e intensidad y que sean distintos? Razona la respuesta. Pon ejemplos
3. a) Si las direcciones de dos vectores convergen ¿podrán ser iguales los vectores?
b) Dos vectores son paralelos y tienen la misma intensidad. ¿Han de ser iguales?
Razona las respuestas. Pon ejemplos.
4. Dibuja en tu cuaderno tres vectores iguales y tres vectores distintos
5. a)Las componentes de un vector son 5 en el eje x y -4 en el eje y. ¿cuánto vale su intensidad (módulo)?
b) ¿Cuál de los siguientes vectores tiene mayor intensidad? (3,0); (2,1); (2,2); (3,2).
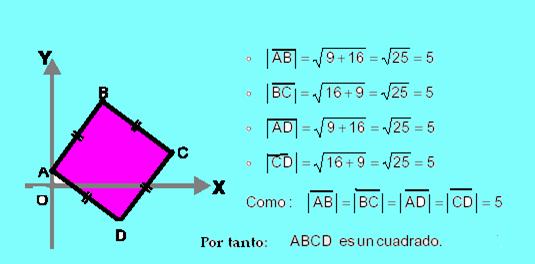
c) Demostrar que los puntos A (0, 1), B(3, 5), C(7, 2) y D(4, -2) son los vértices de un cuadrado
Solución
a)La intensidad o módulo del vector es: 
c) Se verifica :
6. a) Dados los vectores (1,2) y (0,-3) ¿cuál es el resultado de su adición?
b) Con los vectores v(1,2);w(2,-1) y u(-1,1) realiza las sumas: u + v + w , v + u + w . ¿Qué observas?
Solución
b) u + v + w = ( 2, 2); v + u + w = (2, 2). Son iguales, la suma es conmutativa.
Comprueba el resultado gráficamente
7. a) ¿Cuál será el vector opuesto del vector (1, 2)?
Con los vectores del segundo ejercicio anterior , realiza las sustracciones
u - v , v – u, u - w.
8. Suma en tu cuaderno, de forma gráfica (2,1)+(-1,1)+(-2,0).
Realiza la suma anterior de forma analítica.
9. Dados los vectores v(1,2) y w(-2,1), ¿qué vector deberé sumar a v + w para obtener el vector (0,0)?
Solución
El (1, -3), pues tendrá que ser el opuesto de la suma v + w = (-1, 3). Comprueba la afirmación haciendo la suma gráficamente
10 Dados el punto P(1,-2) y el vector v =(-1,3)
obtener:
a) Las ecuaciones vectorial, continua, general y explícita de la recta r que
pasa por P y tiene como dirección v.
b) Obtener tres puntos de la recta distintos de P.
c) Comprobar si los puntos A(6,7), B(2,-5) y C(4,-1) son puntos de la recta r o
no.
d) Representar la recta r.
Solución
a) x = (x, y) = (-1, 2) + t (-1, 3) ecuación vectorial
Eliminando el parámetro se llega a la
ecuación continua: 
De donde obtenemos la ecuación cartesiana:
3(x +1)=-(y-2) 
3x +y = -1
Despejando obtenemos la ecuación explícita: y = -3x -1
11. Halla gráficamente la pendiente de la recta que pasa por los puntos A(-3, -6) y B((3, -2) y escribe su ecuación.
Solución
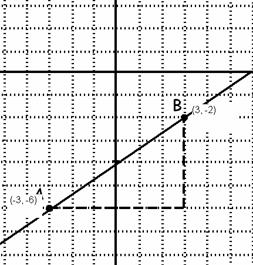La
pendiente según se ve en la gráfica es
la ordenada en el origen es -4
y por tanto la ecuación es
12. Halla la pendiente de las rectas que pasan por los puntos:
a) (2. 3) y (-1, 0)
b) (3, 1) y (4, -5) . Solución 
13. Dibuja y halla la ecuación de la recta que pasa por los puntos:
a) (2. 3) y (-1, 0); b) (3, 1) y (4, -5)
14. Hallar la ecuación de cada una de las siguientes rectas:
a) Pasa por el punto (0, 1) y tiene por pendiente 3
b) Pasa por el punto (0, 4) y tiene por pendiente 3/4
c) Pasa por el punto (-3, 3) y tiene por pendiente -4
15. Halla la pendiente de las rectas:
a) y =
-3x +1; b) y = 2-x; c) 3x-2y-4=0; d) 
16. a) Obtener la pendiente, la ordenada en el origen y la representación gráfica de la recta que pasa por los puntos P(1,2) y Q(5,-1).
b) Obtener la ecuación explícita y la general de la recta paralela a r que pasa por (0,-1).
Solución (Puede abordarse el problema de varias formas)
a) La ecuación de la recta que pasa por
los puntos P y Q es y = mx +n, como pasa por P y Q se verifica 
que
por reducción nos da pendiente m =-3/4, ordenada en el origen n=11/4
La recta tiene por ecuación explícita 
,
y por cartesiana 3x +4y=11
b) La ecuación explícita de la recta paralela que pasa por (0, -1) es y =(-3/4)x-1 y la cartesiana
3x+ 4y=-4, Comprobarlo y hacer la gráfica
17. a) Obtener la pendiente, la ordenada en el origen y la representación gráfica de la recta que pasa por los puntos P(3,4) y Q(2,1).
b) Obtener la ecuación punto-pendiente de la recta paralela a r que pasa por (0,-2).
18.. Dados los puntos A(1, -3), B(2, 0) y C(-4, 1) se pide:
a) Ecuación de la recta r que pasa por A y B.
b) Ecuación de la recta paralela a r que pasa por C.
Solución (se puede hacer de varias formas)
a) el vector AB tiene de coordenadas (2, 0)-(1, -3)= (1, 3), luego la ecuación de r es:
b) la paralela que pasa por C tiene por ecuación 
19. Encontrar la ecuación de la recta r paralela a 2x-3y =4 que pasa por el punto de intersección de las rectas s y t de ecuaciones y =3x-1 , x +2y=-3
20. Encuentra la ecuación de la recta que tiene por dirección el vector v(-1, 3) y pasa por el punto de corte de las rectas de ecuaciones x + y =1 y 2x-3y=0
21. a) Calcular las coordenada del punto B
de un segmento 
, sabiendo que las
coordenadas de A son (2, 6), y las del punto medio M son (4, 5)
b) Calcular la recta paralela a 2x +y-1=0 que pasa por el punto A(1, 1)
Solución
a) El punto medio del segmento tiene por
coordenadas: (m1, m2) =
, luego se
tendrá (4, 5)= 
, es decir tendremos que
8=2 +b1 , de donde b1= 6. Análogamente b2=4
(comprobarlo)
b) El haz de rectas paralelas es de la forma: 2x +y
+c = 0 y como queremos la que pasa por el punto A(1, 1) 2.1+1
+ c = 0, c =-3
SI NECESITAS TEORÍA DE ESTE TEMA VISITA EL “RESÚMEN TEÓRICO”
Cuaderno de actividades 4º ESO
