Cuaderno de actividades 4º ESO

Álgebra

 Expresiones Algebraicas.

 Traduce a lenguaje algebraico:

1. El triple de un número.

2. La mitad del resultado de sumarles al triple de un número 4 unidades.

3. La diferencia de los cuadrados de dos números de dos números consecutivos.

 

4. Cinco veces el resultado de restarle al doble de un número 5 unidades

Solución:      5(2x-5)

5. Expresa algebraicamente el área y el perímetro de un cuadrado de lado x.

 

 

 


         x

 Asocia cada una de los enunciados con la expresión algebraica que le corresponde:

 

1) La suma de los cuadrados de dos números

 

2) El espacio recorrido por  un móvil es igual a su velocidad por el tiempo que está en movimiento

 

3) El área del circulo de radio x

 

(x +y)2= x2+ y2+ 2xy

 

4) Los lados de un triángulo son proporcionales a 2, 3 y 5

 

E = v .t

5) El cuadrado de la suma de dos números es igual a la suma de sus cuadrados más el doble de su producto

 

x2+ y2       (1)

 

6) Media aritmética de tres números

 

Px2    

 

C) Calcula el valor numérico de las siguientes expresiones para los valores que se indican:

1. (1-2x)(1+ 2x)  para x = 2

 

2.       para x =3, y =2, z =4

Solución ==3

3. x2+ y2+ 2xy             para x =1, y =2

 

D) Identidades notables.

Cuadrado de una suma                        

Cuadrado de una diferencia                

Diferencia de cuadrados                     

 

1) Desarrolla las siguientes expresiones:

a) (2x +3)2

b) (x +2)(x –2)

c) (2x –1)(2x +1)

d) (3x – y)2

e) (2x –3y)(2x +3y) = 4x2 –9y2

h) (x -1)3

i) (x +5)2-(x-3)2

2) Factoriza las siguientes expresiones algebraicas:

a) 3x4 -2x2

b) x2 –1

c) x2 +6x +9 

Solución. No tiene ningún factor común , es una identidad notable: (x +3)2= x2 +6x +9

d) x2 + 4 +4x

e) 4x2-y2

f) 9 –6x +x2

g) 2x –4x2y

h) x2 +x y +x z +y z

Solución: x(x +y) +z(x +y) =(x +z) (x + y)

i) a x –ay –b x +by

3) Completa las siguientes expresiones para que sean cuadrados perfectos

a) x2+ 2x+.....

b) 4x2 + 8x+......

Solución:      4x2 + 8x +4 = (2x +2)2

c) 9x2 -....+ 16

 Polinomios

Indica el grado de los siguientes polinomios:

1. –2x2y3                                            2. . x2+ y2+ 2xy

 

3.    Solución:      2+4+2 =8

4.  (x +5)2-(x-3)2

5. 7x5-3x2-6x4+ 2+ x

Efectúa las operaciones indicadas y simplifica la expresión resultante.

1) 3(x3 –5x +7) –(2x3 +6x2 +11x+4)

2) 2x(4x2 –6x +2) +3 (5x2 –3x-4)- 14 x2

3) (x3y3 + 2) (x3y3 - 2)

4) (7x3 –5x+3) (2x2 +x-1)

 

5)

Solución:  = 4x-12 +21x-9-24 = 25x -45

6)

 

7) Multiplica por 12 y simplifica el resultado

8) Multiplica por 20 y simplifica el resultado:

2

 División de polinomios.  Ruffini

Divide los siguientes polinomios:

1) 15 a3b2c : 6 a2c ==

2) 5 x3y2z4 : 3 x2z2

 

3) (x4 -6x3 +5x2-4x+1): (x2 –3x +1)

Solución

x3 + 6x2  +5x +4      x2 –3x +1

-x3 +3x2 -x         x +9

/       9x2 + 4x +4

       -9x2 + 27x-9

           /    31x –5

 

4) (x3 +6x2 +5x+4): (x2 –x +5)

5) (x4 -5x3 +3x2-2x+5): (x2 +x -3)

Nota. Cuando el divisor es un binomio de la forma (x-a) se puede aplicar la regla de Ruffini, que utiliza sólo los coeficientes[C1] 

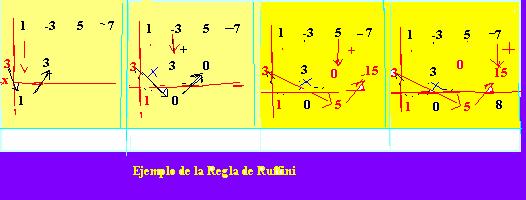
Ejemplo. Divide  x3-3x2+ 5x-7 entre (x-3)

Se hace la siguiente disposición de la figura. El cociente es x2+5 y el resto 8

6) (x3 –x2 -16x -3): (x -3)

Solución: Utilizando Ruffini quedaría

Nos queda que el cociente es x2 +2x – 10        y el resto -33

7) (2x3 +6x2 +11x+4):(x +1)

8) (3x4 +6x2 +11x+4) : (x-2)

9) (x3 + 1) : (x +1)

10) (–x4 +2x3 +5x -3):(x+3)

Raíces de polinomios

El valor numérico de un polinomio en x = a es el que se obtiene al sustituir la indeterminada por a.

Las raíces o ceros de un  polinomio son  los valores que lo anulan.

1. Calcula el valor numérico de los siguientes polinomios en los números que se indican.

a) x2 -5x +6   en x =0, 2 y 3

 

b) 2x4 -6 x2 +3x-2  en x = 1 y  3

2. Comprueba si  de los valores que se dan son raíces de los siguientes polinomios:

a) x2 +1         0, -1

Solución.      Para 0 el valor numérico del polinomio es 1, luego no es raíz

                   Para -1 “                         “               2          “

b) x2 -5x +6   0, 2 y 3

 

c) x2  -4        2 y .-2

 

d) x3 -1        -1, 0, 1 y 2

3. Calcula las raíces de los siguientes polinomios.

a) x2 -5x +6

Solución. El valor numérico del polinomio en 2 y 3 nos dio 0, luego las raíces son 2 y 3

Comprueba usando Ruffini

b) x2 -2x +1

 

c) (x3 -1) : (x-1)

Aplicamos Ruffini

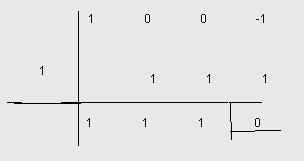
El cociente es        x2 + x + 1,     el resto 0.

La única raíz es x = 1, pues el cociente no tiene ninguna raíz

d) x3 -11x2 +34x -24

e) x4 -11x3 +33x2 -9x -54

Teorema del resto ( o teorema del residuo)

El resto de la división de un polinomio P(x) entre el binomio (x-a) es el valor numérico del polinomio en x =a, es decir el resto es el valor de P al sustituir la x por a, R =P(a).

Demostración:

Por el algoritmo de la división entera: Dividendo = Divisor x Cociente + Resto,

Se verifica P(x) = (x-a)C(x) + R, si sustituimos la x por a, nos queda,

P(a) =(a-a)C(x)+R = 0 +R, es decir,  P(a) = R

Aplicación: Sirve para calcular el resto sin efectuar la división

4. Calcula el valor de k para que la división de P(x) entre Q(x) dé exacta:

a) P(x) = ) x3 -11x2 +k.x -24, Q(x) = (x-1)

El resto debe dar cero, aplicando el teorema del resto:

P(1)= 13 -11.12 + k.1 -24 = 0, luego        k = 34

b) P(x) = x4 -11x3 +33x2 –k x -54; Q(x) = (x +1)

5. Calcula el valor de k, para que el resto de la división de x4 –k x3 +33x2 –k x -54 entre x +2 nos de 25.

Factorización

Factorizar un polinomio es ponerle como  producto de sus factores (se llama también descomposición en factores del polinomio).

Por ejemplo, si el polinomio solo tiene raíces reales y simples (r1, r2, ....rn,  quedará de la forma:

P(x)= A(x-r1)(x-r2)....(x-rn)

Para factorizar hay que tener en cuenta las identidades notables, el sacar factor común,  la regla de Ruffini,  y la resolución de ecuaciones (de 2º grado) para la búsqueda de raíces.

6.1 Descomponer en factores:

a) x2 -2x +1

b) x3-5x2+ 4x

Solución

En primer lugar se saca factor común x, x3-5x2+ 4x =x(x2-5x+4)

El segundo factor es un polinomio de 2º grado, y para encontrar los otros factores se puede obtener las raíces aplicando la fórmula de la ecuación de 2º grado.

 x =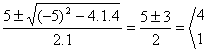          por tanto los factores son (x-4) y (x-1)

El polinomio factorizado es: x(x-4)(x-1).

Nota: También podría haberse usado Ruffini para el cálculo de las raíces, ya que son enteras

d) x3 -11x2 +34x -24

e) x4 -11x3 +33x2 -9x -54

 

6.2 Descomponer en factores los polinomios P(x) y Q(x) y hallar su M .C .D  y  M . C . M

a) P(x) = x3 -1 y Q(x) = x2 -2x +1

Solución

P(x) = (x – 1) (x2 + x + 1)

Q(x) = (x -1)2

M. C. D.  = x-1                 M. C. M. = (x-1)2(x2 + x + 1)= x4 –x3-x+1

b) P(x) =3x3+ x2-8x+4 y Q(x) =3x3 +7x2-4

7. P(x) = x7 –x            y    Q(x) = x5 +x2

 Fracciones Algebraicas

A) Hallar el valor numérico de las siguientes fracciones algebraicas en los puntos que se indican:

1)       en x = 1, x =3.

2)      en x = 2, x = 0.

 3)     en x =1, x =2

Solución:

En      x = 0  No existe este valor, se puede dividir por cero,  no se puede calcular el valor numérico en 0.

En      x =2  

4) en x =-2,  0, 1 y 2

B) Estudia si las siguientes fracciones son equivalentes:

1)  y

2)   y

Solución. Se tiene:

(x-2)(x2-4) = x3 -4x -2x2+8 = x3 -2x2 -4x +8

(x +2)(x2-4x+4) = x3 -4x2 +4x+ 2x2 -8x +8 = x3 -2x2 -4x +8

Son equivalentes.

C) Simplifica las siguientes fracciones algebraicas, en los casos posibles:

1)

2)

3)

4)

5)

Solución.

Se tiene =

6)

D) Realiza las operaciones indicadas y simplifica el resultado en los casos que se pueda.

1) .

2)

3)

 

4)

Solución. Primero reducimos a común denominador y después sumamos los numeradores:

m .c. m (x, x +1) = x(x +1) =x2+ x

=

 

5)

 

 

6)

7)

8)

 

Si quieres ampliar el tema te aconsejo que visites Álgebra

       

VOLVER

Cuaderno de actividades de 4º ESO

 

 [C1]Ver ejemplo 6