ARITMÉTICA[1]
OPERACIONES CON NÚMEROS :
A) ENTEROS
Realiza las siguientes operaciones:
1) 
2) 
3) 
4) 
5) 
6) (16) : (-2)+4(3-1)+9 = -8 + 4.2+9 = - 8 +8 +9 =9
7) (-12): (3)+3.5-6(8-3)
8) 15: [(-12): 4]+5
9) –3+(5-3.7)+(3)2
10) (-2)3+(5.6-8)-2
11) 
12) 4-3(-2)3-5{(-3)2(-1)5+7.2-3(7-2)+1}
11. Solución Seguimos las reglas de las operaciones
Efectuamos los paréntesis 2(-1)4+(-2)3+82-3(2)
“ las potencias 2.1+(-8)+64-3(8)
“ los productos 2-8+64-24
por último las sumas y restas 66-32=34
B) RACIONALES: FRACCIONES Y DECIMALES
a) Calcula:
1) 
de 120
2) 
de 3600
3) La mitad de 
4) La tercera parte de 
. Solución 
5) La mitad de la quinta parte de –15
6) Cuánto dinero tengo si los 
de éste
son 34 euros.
7) Tres fracciones equivalentes a: 
, 
.
8) Calcula x, en cada caso, para que las igualdades sean ciertas:
;
; 
9) Calcula el 20% de 375 euros.
8). Solución. Como son fracciones equivalentes, x =3.7=21; x =7.5=35; x = 5.3=15
b) Reduce a común denominador[2] las siguientes fracciones
1) 
2) 
3) 
4) 
y
5)
3. Solución. El m.c.m. (3, 5, 2)=30.
Es decir: 10/30; 12/30 y 45/30
c) Ordena de menor a mayor las siguientes fracciones
1) 
2) ,
3) 
4) 
1) Una vez que hemos
encontrado fracciones con igual denominador equivalentes, ordenamos los
numeradotes: 10/30;
12/30 y 45/30 es decir: 
d) Simplifica las siguientes fracciones
1) 
2) 
3) 
4) 
5) 
6) 
5) Solución. 
e) Calcula:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
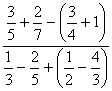
9. Solución.
=
f) Encuentra la fracción generatriz de los siguientes números:
1) 0,03 2)
3) 
4) 
3) Solución. Si hacemos
N=
10N=
100N=
Restando los dos números que tienen el mismo periodo, éste se “va”:
100N-10N=
-
90N =112ÞN =
g) Calcula pasando a fracción:
1) 
2) 
3)
h) Representa los siguientes números racionales:
2/3; -3; 7/5; -3/4, 12/8
1/3 2/3
i) Escribe en forma decimal o fraccionaria las siguientes expresiones:
1) Dos quintos.
2) Tres de cada cinco.
3) Mitad de cuarto.
4) Dos partes por mil.
5) Tres partes de agua y dos de alcohol.
6) Escala 1 a
200000. Solución1:200000
se expresa 
7) 13 décimas.
8) 234 centésimas.
9) Una millonésima.
C) NÚMEROS REALES. APROXIMACIÓN. INTERVALOS.
a) Di cuáles de los siguientes números son racionales y cuales son irracionales:
1) 
2) 
;
3) 
; 4) 
;
5) 
6) 
7) 3,56565656...... 8) 3,141592.....
9) 0,30300300030000.... es irracional las cifras decimales no se repiten, es decir no es periódico
10) –3,45454545.....
b) Calcula, sin usar la calculadora, las siguientes raíces exactas:
1) 
; 2) 
;
3) 
4) 
5) 
6) 
7) 
8) 
6)
Solución. 
=
c) Calcula por tanteo, sin usar la calculadora, una aproximación decimal de los siguientes números irracionales:
1)
2) 
;
3) 
4) 
2) 62=36; 72=49, luego está entre 6 y 7 6,82=46,24
6,92=47,61 Con un decimal la aproximación seria 6,8
6,842=46,78;
6,852=46,92; ,6,862=47,05. Luego 
=6,85 con dos decimales exactos
d) Halla las raíces posibles y di cuáles son imposibles y por qué:
1) 
2) 
3) 
4)
5) 
no existe pues el índice es par y el
radicando negativo
e) Escribe tres aproximaciones decimales de los números irracionales
1) 2)
f) Calcula
la cota del error que se comete al sustituir el número por:
1) 3,14
2) 3,142
Solución. Tiene tres cifras decimales exactas, luego el error que se comete es menor que 10-3
3) 3,1415
g) Escribe las aproximaciones por defecto del número 
, con la
mínimas cifras para que el error cometido sea menor que:
1) una décima.
2) una milésima
h) Calcula el lado de un cuadrado, cuya área es 1500 m2 , con un error menor que una centésima.
i) Escribe en forma de desigualdad y representa los siguientes intervalos:
1) [-3, 2]
2) (1, 3)
3) [-1, 0)
Solución. [-1,
0)=
-1é ö0
k) Escribe en forma de intervalo y representa los conjuntos:
1) 
2) 
3) 
D) POTENCIAS
a) Hallar el valor de las siguientes potencias:
1) (-3)3 2) 5-2
3) 
4) 
5) (-3)2.3-3 6) 52.5-3.57.5-4
7) 
8) 
8) Solución. 
=
=3-8.2-1
b) Escribe en forma de potencia de una sola base:
1) 625 2) 128
3) 
4) 
5) 
6)
5) 
=
c) Expresa como potencia única:
1) (5-3.52)-6 2)
3) 
4) 
*5) 
4) Solución. 
d) Simplifica:
1) 
2) 
3) 
4) 
3) Solución. Primero reducimos las potencias a bases positivas
=+
=782-75-2
e) Escribe como potencia de 10
1) 0,00001= 10-5
2) una millonésima
3) 1000000000
f) Indica el orden de magnitud [3]de las siguientes medidas:
1) El volumen de la Tierra: 1,0807.1021m3
2) La masa del Sol: 1,98.1030kg
3) La masa de un electrón: 1,67.10-27kg
g) Escribe con notación científica::
1) 310000000000
2) 0,00000023=2,3.10-7
3) 1540,23
4) El número de moléculas que hay en un gramo de hidrógeno: 301000000000000000000000
5) La longitud de un paramecio: 0,000025 m
h) Expresa en forma decimal:
1) 3,23.10-7
2) 1,75.108
3) La masa de un electrón: 1,67.10-27kg
4) El precio de una casa: 3,24.107 =32400000
5) El volumen de la Tierra: 1,0807.1021m3
6) La masa del Sol: 1,98.1030kg
i) Realiza las siguientes operaciones:
1) 2,43.10-23.1,35.1021
2) (3,21.107): (2,51.10-4)
3) 
4) 
3) Solución. 
=
=9,79.1013
j) Escribe en forma científica con tres cifras significativas los siguientes números:
1) 0,0000000000000002567432
2) 1234567891234
k) Empleando diversas técnicas de conteo, se han obtenido los siguientes datos:
- Visitantes anuales a un cierto museo: 1 345 589 personas.
- Número de gotas de agua que hay en una piscina: 8 249 327 141 gotas.
- Bacterias en 1 dm3 de cierto preparado: 203 305 123 bacterias.
¿Es razonable dar tantas cifras? ¿Cómo transmitirías tú cada una de estas informaciones?
E) RADICALES
a) Completa siguiendo el modelo:
1) 
2) 
=
3) 
=
b) Extrae factores del radical siguiendo el modelo:
1) 
2) 
3) 
4) 
c) Suma las expresiones con radicales (que puedas):
= 
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
Ayuda. Recuerda que los radicales solo se pueden sumar cuando son semejantes[4].
d) Opera los siguientes radicales y/o simplifica cuando sea posible:
1) 
2)
3) 
4)
5) 
6)
7) 
8)
9) 
10)
3) Solución.
Se reducen a índice común y después se multiplican los radicandos.
m.c.m(2,3)=6 
=
=
e) Calcula los valores de las siguientes potencias (de exponente fraccionario) o radicales:
1) 
2)
3) 
4)
23.33
5) 40,5 6)
7) 
8)
6250,25
9) 
Recuerda que 
f) Racionaliza[5] siguiendo el modelo:
=
|
1) |
5) |
|
2) |
6) |
|
3)
|
7) |
|
4)
|
8) |
g) Representa en la recta real los números irracionales
1)
2) 
3) 4)
2) Solución . Utilizamos el Teorema de Pitágoras. 5 = 12+22
1 
es la diagonal del triángulo, con un compás de origen 0 se obtiene
donde está situado
2
.
h) Simplifica los siguientes radicales:
|
1 )
|
2) |
|
3) |
4) |
|
5) |
4) |
4) Solución: 
=
=
i) Expresa en forma de una sola potencia de exponente fraccionario:
|
1) |
2) |
|
3) |
4) |
|
5) x3 |
6) |
3). Solución
= 
; 5) Solución. x3
= 
=
=
Problemas[6]
1. Tengo tantas hermanas como hermanos, pero mis hermanas tienen la mitad de hermanas que de hermanos. ¿Cuántos somos?
2. Nos gastamos 1/3 de nuestra paga en el cine; 1/8 de lo que nos queda en palomitas y por último 1/4 de la parte restante en bebidas.¿Cuánto tenemos de paga?
3.Los 4/7 de un segmento superan en 3cm la mitad del segmento. ¿Cuánto mide ese segmento?
4.La diferencia de edades entre un padre y su hijo es de 30 años, la edad del hijo es 2/5 de la del padre. Que edad tiene cada uno?
5. Una pista de carreras de atletismo se divide en tres tramos desiguales. La longitud total de la pista es 450 m. La longitud de los tramos primero y segundo juntos es 350 m. La longitud de los tramos segundo y tercero juntos es 250 m. ¿Cuál es la longitud de cada tramo?
6. Anteayer tenía 17 años y el año que vienen cumpliré 20 años. ¿Cómo es posible?
7. Una sierra en un aserradero corta largos troncos, de 16 m de longitud, en troncos cortos, de 2 m. de longitud. Si cada corte se hace en dos minutos, Cuánto tiempo se necesitará para que la sierra produzca los ocho troncos cortos a partir de un tronco largo.
8. Un bidón lleno de queroseno pesa 8 Kg. Se derrama la mitad del queroseno, después de lo cual bidón y contenido pesan 4 Kg. y medio. Determinar el peso del bidón vacío.
9. Un pasajero al llegar a la mitad de su viaje cae dormido. Cuando despierta, aún tiene que recorrer la mitad de la distancia que ha hecho mientras dormía ¿Qué parte del total del camino ha estado durmiendo?.
10. El ser vivo más pequeño es un virus que pesa del orden de 10-18 g y el más grande es la ballena azul, que pesa aproximadamente 138 toneladas. ¿Cuátos virus serian necesario para conseguir el peso de una ballena?
11. . Con 2 km3 de arcilla se construyen dados de un cm3. ¿Cuántos se pueden construir?. Si colocamos todos estos dados en fila india, es decir, uno a continuación de otro, ¿qué longitud alcanzarían?
12. Al principio, el precio de un Kg. de azúcar era tres veces el precio de un Kg. de sal. Después, el precio de un Kg. de sal aumentó en la mitad de su anterior precio, sin que cambiara el precio del azúcar. Si el precio de la sal es ahora 30pts. por Kg., ¿cuál es ahora el precio del azúcar por Kg.
13. La masa de un virus es de 10-21kg, la de un hombre, 70kg, y la de la Tierra 5,9 x 1024kg. Calcula la relación entre la masa de un hombre y un virus, y la de la Tierra y un hombre. ¿Cómo son estas relaciones?
14. Tres amigos coinciden en un restaurante. Comentan que todos van habitualmente. Uno de ellos va cada 5 días, otro cada 6 y el otro cada 9. ¿al cabo de cuántos días volverán a encontrarse?.
15. En una cooperativa tienen 360 litros de un cierto tipo de aceite y 225 litros de otro tipo. Quieren envasar el aceite con el menor número posible de garrafas iguales ¿Qué capacidad tendrá cada garrafa?
16. Diez ciruelas pesan tanto como tres albaricoques y un mango. Seis ciruelas y un albaricoque pesan lo mismo que un mango. ¿Cuántas ciruelas equilibrarían una balanza que tiene en un lado un mango.
17. Un ciclista sale de un lugar a 20km/h. Dos horas más tarde sale un coche del mismo lugar a 80km/h. ¿Cuánto tiempo tardará el coche en alcanzarle?
18. El precio de un artículo sin IVA es de 750 euros. Si he pagado 840euros. ¿Qué porcentaje de IVA me han cobrado?
19. Un cobrador se queda con el 0,5% de la cantidad recaudada. Si le ha correspondido 6250 euros, ¿cuánto ha cobrado?
20. a) ¿Qué índice de variación corresponde a un aumento porcentual del 15%? ¿ Y a una disminución porcentual del 17%?
b) El número de parados, 356 230, que había en una determinada comunidad autónoma ha disminuido el 17 %. ¿Cuántos parados hay ahora?
c) Después de distribuir el 27% de las cajas que había en un almacén han quedado 27250. ¿Cuántas cajas había?.
21. Se mezclan 20litros de aceite de oliva de 2,2 euros el litro, con 13litros de aceite de semillas a 1,3 euros el litro. ¿A cuánto sale el litro de la mezcla?
22. Para la fabricación de queso se mezcla un 60% de leche de vaca con un 40% de leche de oveja. El precio de la leche de vaca es de 0,85 euros el litro y el de la leche de oveja es de 1,2 euros el litro. Para fabricar un queso se necesitan 8 litros de leche. ¿A qué precio saldrá la mezcla?
23. Reparte 6000 euros en partes proporcionales a 2, 3 y 5.
24 Tres socios pusieron 20 millones, 30 millones y 60 millones, respectivamente, para crear una empresa. A) ¿Qué parte de las ganancias corresponderá a cada uno?. Si las ganancias del primer año fueron 7590000. ¿Cuánto corresponderá a cada uno?
25. Un grifo llena un depósito en 2 horas, y otro grifo lo llena en tres horas. ¿Cuánto tardará en llenarse el depósito si se abren ambos grifos a la vez?
26. Tres grifos aportan caudales de 2 l/s, 3 l/s y 5 l/s, respectivamente. Se abren los tres a la vez para llenar un balsa.
a) ¿Qué fracción de la misma habrá aportado cada uno?
b) Si la balsa tiene una capacidad de 6000 litros qué volumen de agua ha manado de cada grifo?
27. Un grifo arroja 70l de agua por minuto y otro arroja 50l por minuto. ¿Cuánto tiempo tardarán en llenar entre los dos un depósito de 360l?
28. Tres personas trabajando 8 horas diarias hacen un trabajo en 15 días. ¿Cuántos días tardarán en hacer el mismo trabajo cinco personas en jornadas de 9 horas?
29. . Construye un cuadrado mágico 3x3. ( Sobre un cuadrado de nueve casillas deben colocarse nueve números distintos, del 1 al 9, de tal modo que la suma de las columnas, de las filas y las diagonales deben dar lo mismo).
30. Calcula la diagonal de un cuadrado de lado 5
TECNICAS DE CONTEO. COMBINATORIA
Resuelve:
31 Ignacio tiene 3 pantalones y 5 camisas. ¿cuántas indumentarias puede elegir?
32 De cuántas formas distintas se pueden colocar 4 personas en un banco de 4 asientos.
33 En un coche viajan 5 personas. ¿De cuántas formas distintas pueden ir sentadas?¿Y si solo dos de ellas saben conducir?
34 Se lanzan dos dados ¿cuántos resultados distintos pueden dar?
35 ¿De cuántas formas se pueden repartir tres medallas entre 12 participantes de una carrera?
36 Se lanzan 5 monedas sobre la mesa ¿de cuántas formas pueden salir dos caras?
37 ¿Cuántos números de tres cifras se pueden formar con las cifras pares?
38 ¿De cuántas formas se pueden repartir tres camisetas (iguales) entre 6 amigos sin que ninguno pueda llevarse más de una?
39 ¿De cuántas formas pueden sentarse 3 personas en un banco de 5 asientos?
40. ¿De cuántas formas se pueden elegir dos cartas de una baraja de 40 cartas?
Soluciones de los problemas seleccionados
1. Solución.
4 hermanos y 3 hermanas
3. Solución
Dividimos el segmento en 7 partes iguales
1/14
½ ½ ½ ½ ½ ½ ½ ½ ½
Por tanto 1/14 del segmento es igual a 3cm Þ el segmento medirá 3.14= 42cm
6. Solución.
Estamos a 1 de enero y nací el 31 de diciembre
8. Solución.
.
8kg 4,5kg
El líquido derramado pesará 8 - 4,5 = 3,5
El líquido en total pesará 7kg, luego el bidón vacío pesa 1kg.
12. Solución
30 = precio anterior + 1/2 del precio anterior
30= 3/2 del precio anterior Þ
precio anterior de la sal = 30.2/3 = 20
precio del azúcar 3.20 = 60pts
14. Solución.
Se encontrarán en un múltiplo común a todos.
m.c.m.(5,6, 9, )=90
Se encuentran a los 90 días
18. Solución.
Aplicamos en concepto de índice de variación.
Se tiene CF = CI. IV, luego el índice de variación en esta operación es:
IV =
=1,12
Como 1,12=1+0,12 Þ que se ha aplicado un 12% de IVA
21. Solución.
Se mezclan en total: 20 +13 = 33 litros
20.2,2 +13.1,3 = 44 + 16,9 = 60,9 es lo q se paga por los 33 litros.
El litro de la mezcla sale a 60,9:33 =1,85 euros
23. Solución.
Consideramos el capital dividido en 2 +3 +5=10: partes.
De las cuales dos partes le corresponderían al primero,. tres partes al segundo y cinco partes al tercero.
Al primero le tocan los 2/10 de 6000 euros.
Al segundo, los 3/10 de 6000 euro.s
Al tercero, los 5/10 de 6000 euros.
Luego les tocará 1200, 1800 y 3000 euros respectivamente
25. Solución
Si en 2 horas llena un grifo el depósito, en una hora llenará 1/2 del depósito
El otro grifo en una hora llenará 1/3 del depósito.
Los dos juntos en una hora llenarán:
1/2 + 1/3 = 5/6 del depósito
Luego para llenar el depósito se necesitaran 
=1,2 horas es decir una hora y doce
minutos.
28. Solución.
En hacer el trabajo se tardan:
3x8x15=360 horas
Entonces se necesitarán 360:(9x5) =8 días
30. 5
Por el teorema de Pitágoras:
d2
=52 +52=50Þ d=
38) Solución
Como son iguales el orden no importa, además no pueden repetirse, son combinaciones, C6, 3 = 20 Þ hay 20 formas de repartirlas
