EJERCICIOS PROPUESTOS DEL TEMA: POSICIONES RELATIVAS Y PROBLEMAS MÉTRICOS EN EL ESPACIO
1.
Determinar la posición relativa de la recta r:
y el plano 
x+2y+4z=13
2.
Determinar el parámetro k para que la recta r: 
sea
paralela al plano 4x+ky+z-2=0
3.
Hallar la ecuación del plano que contiene a la recta r: x-2 =y-3= z y es
paralelo a la recta s:
4.
Hallar el ángulo que forma la recta 
con el plano 3x+2y-4z+6=0.
5.
Hallar el ángulo que forman las rectas r: 
y s: 
6. Hallar el
ángulo determinado por los planos 
y 
0
7. Hallar la
ecuación de la recta r que pasa por el punto P(1, 1, -3) y es perpendicular al
plano x-2y
+z +2=0
8. Hallar la
distancia del punto P(5-1, 6) a la recta r: 
9.
Hallar la distancia del punto P(2, 1, -5) al plano : x+2y-5z+4=0
10.
Calcula la distancia entre las rectas r: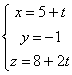 
y s:
11.
Probar que las rectas r:
y s: 
se
cruzan y calcula la distancia mínima entre ellas.
12. Dados el punto O = (0,0,0) y el plano 
: x+y+z = 6, se pide
calcular razonadamente:
a) La ecuación de la recta r que pasa por O y es
perpendicular al plano
b) Las coordenadas del punto simétrico de O
respecto del plano
c) La ecuación del plano que contiene al eje X y a la recta r
13. Considera los planos p1 : 2x + ay + 4z - 1 = 0 y p2: ax + 2y + 4z - 3 = 0.
a) Calcula el ángulo que forman p 1 y p2 cuando a =1.
b) Halla a para que p1 y p2 sean paralelos.
c) Determina el valor de a para que p1 y p2 sean perpendiculares.
14. Dados las rectas r: 
y
s: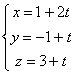 
se pide:
a) Explicar de un modo razonado cuál es la posición
relativa de las rectas r y s y la posición relativa de la recta
s con el plano
b) Calcular la distancia entre las rectas r y s
y el ángulo entre la recta s y el plano
15. a) Calcula el valor de m para que las rectas r y s sean coplanarias:
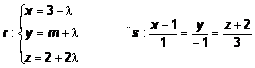
b) ¿Cuál será la posición relativa de r y s para ese valor de m?
16. Dada la
recta r :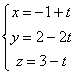 
y el plano :
2x+y=4 se pide:
a) Posición
relativa de r y
b) Hallar la
distancia de r a .
