Esta página está en construcción, volver

 

 

Si necesitas teoría visita GEOMETRÍA DEL ESPACIO

 

 

SI PREFIERES VERLO EN DOCUMENTO DE WORD

 

 

 

SOLUCIONES A LOS PROBLEMAS PROPUESTOS

 

 

1. Determinar la posición relativa de la recta  r: y el plano x + 2y+4 z =13

Solución

El vector de dirección de r es u (2, -5, 2)  y el vector normal al plano es n (1, 2, 4).

u. n = 2-10+8= 0 luego las rectas son paralelas o coincidentes (ver teoría).

Como A(1, -5, -3) no pertenece al plano, pues 1-10-12-13 =-34 0 concluimos que son paralelas .

 

2. Determinar el parámetro k para que la recta  r: sea paralela al plano

4x+ky+z-2=0

Solución

Para que la recta sea paralela al plano se tiene que verificar que u. n= 0

(2, 4, 2).(4, k, 1)= 8 +4k+2=0 , es decir 4k= -10 de donde k= -5/2

 

3. Hallar la ecuación del plano que contiene a la recta r: x-2 =y-3= z    y   es paralelo a la recta s:

Solución

 Dicho plano tendrá como vector director n a u x v donde u y v son los vectores de dirección de las rectas r y s

u=( 1, 1, 1) , v((2, 1, 4)

n = u x v = 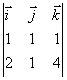=(-3, -2, -1) 

El plano tendrá de ecuación   3x-2y –z +d =0. Como contiene a r pasa por el punto  P(2, 3, 0), lo que nos permite determinar d.  6- 6 +d =0  de donde d = 0 y el plano pedido  es 3x-2y –z  =0

 

4. Hallar el ángulo que forma la recta  con el plano 3x+2y-4z+6=0.

Solución

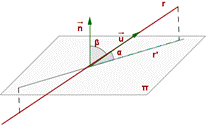
El ángulo entre una recta y un plano es el que forma la recta con su proyección sobre el plano.

Es complementario del que forma la recta con el vector director del plano (ver figura)

 

En este caso y por lo tanto:  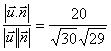 = 0,678

 

47, 30  y 42, 70= 42º42’

5. Hallar el ángulo que forman las rectas r:  y s:

Solución

Si  son los vectores de dirección de las rectas r y s, respectivamente,  entonces el ángulo que forman r y s queda determinado así: cos

(2, 5, -1)  y    *= (2, 3, -5)x(1, -2, 0) = 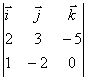=(-10, -5, -7)

 

(*Nota: Un vector de dirección de la recta s se obtiene hallando el producto vectorial de los vectores normales de  los planos que la determinan)

Por lo tanto = 0,5259  y 58,267 =58º16’

6. Hallar el ángulo determinado por  los planos  y 0

Solución

El ángulo que forman dos  planos es igual al ángulo que forman los vectores normales a ellos.

Por lo tanto = = 0,345 y  69, 81 =69º48’

 

7. Hallar la ecuación de la recta r que pasa por el punto P(1, 1, -3) y es perpendicular al plano x-2y +z +2=0

8. Hallar la distancia del punto P(5-1, 6) a la recta r:

9. Hallar la distancia del punto P(2, 1, -5) al plano : x+2y-5z+4=0

10. Calcula la distancia entre las rectas r: 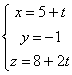    y      s:

11. Probar que las rectas r: y  s:  se cruzan y calcula la distancia mínima entre ellas.

(Repasar siempre los cálculos)