GEOMETRIA DEL ESPACIO (resumen)

VECTORES. PRODUCTO ESCALAR, VECTORIAL Y MIXTO. ECUACIONES DE RECTAS Y PLANOS (en construcción)

POSICIONES RELATIVAS ENTRE RECTAS Y PLANOS. ÁNGULOS DE RECTAS Y PLANOS. DISTANCIAS ENTRE RECTAS Y PLANOS

 

EJERCICIOS PROPUESTOS Y RESUELTOS DEL TEMA

                                              

 

POSICIONES RELATIVAS DE RECTAS Y PLANOS

 

Posiciones relativas de dos rectas

1. Si las rectas tienen la misma dirección, es decir los vectores de dirección, u y v, son iguales o proporcionales, rang (u, v)=1, las rectas pueden ser paralelas o coincidentes

    

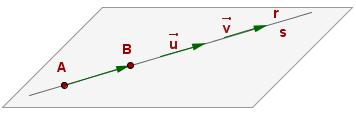
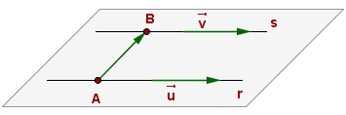
Coincidentes                                       paralelas

 

Si las rectas tienen distinta dirección, es decir rang (u, v)=2,  pueden ser secantes o cruzarse

  

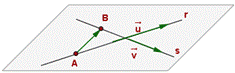
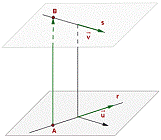
Secantes*                           Se cruzan**

 

*los vectores u, v y AB son linealmente dependientes. rang (u, v, AB)=2

**los vectores u, v y AB son linealmente independientes. rang u, v, AB)=3

 

2. Si las rectas vienen dadas en forma implícita se estudian los rangos de la matriz, A, de los coeficientes y de la matriz ampliada,  AB. Se tiene:

Posición	Rang A	Rang AB
Coincidentes	2	2
Paralelas	2	3
Secantes	3	3
Cruzadas	3	4

 

Posiciones relativas de recta y plano.

1. La recta r viene definida por un punto A y un vector u.

Si n es el vector normal del plano  π se verifica

Posición		A
Recta contenida en el plano	= 0	π
Recta y plano paralelos	= 0	π
Recta y plano secantes	≠ 0

 

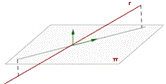
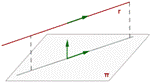recta  contenida  en el plano                               recta paralela al plano                                              recta y plano secantes

 

 

 

 

2. Si la recta  viene dada por sus ecuaciones implícitas, al igual que el plano,  se estudian los rangos de la matriz de los coeficientes, A,  y de la matriz ampliada,  AB. Se tiene:

Posición	Rang A	Rang AB
Recta contenida en el plano	2	2
Recta y plano paralelos	2	3
Recta y plano secantes	3	3

 

Posiciones relativas de dos planos.

Dos planos pueden ser secantes, paralelos o coincidentes. Si los planos están dados por sus ecuaciones implícitas:    ,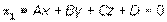 

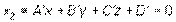
Se tiene:

Posición		Rang A	Rango AB
Secantes		2	2
Paralelos		1	2
Coincidentes		1	1

 

MEDIDA DE ÁNGULOS ENTRES RECTAS Y PLANOS

 

Ángulo entre dos rectas

 Si  son los vectores de dirección de las rectas r y s, respectivamente,  entonces el ángulo que forman r y s queda determinado así: cos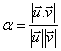

Ángulo entre dos planos

Si  son, respectivamente, los vectores normales a los planos ,  el ángulo que forman dichos planos es igual al ángulo que forman los vectores normales a ellos (vectores directores), es decir: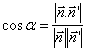   

Ángulo entre recta y  plano

El ángulo entre una recta y un plano es el que forma la recta con su proyección sobre el plano.

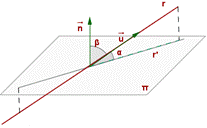
Es complementario del que forma la recta con el vector director del plano.

Por lo tanto si llamamos al ángulo entre r y :   

 

 

DISTANCIA ENTRE PUNTOS, RECTAS Y PLANOS

 

Distancia entre dos puntos

Si P₁(x₁, y₁, z₁) y P₂(x₂, y₂, z₂) son dos puntos del plano la distancia entre ellos es el módulo del vector P₁P_2.  Por lo tanto d  (P₁, P₂) =

 

Distancia entre un punto y una recta

La distancia de un puno P a una recta r es la distancia de P a su proyección, P’, sobre la recta.    d  (P, r)= d (P, P’)

Para calcular esta distancia hay dos métodos:

-Primer método: Se halla el plano  perpendicular  a r que pase por P.  La intersección de y r es el punto P’ buscado.

-Segundo método, basado en la interpretación geométrica del producto vectorial.

 

                      

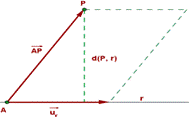
d(P, r)    =         donde R es un punto de r y es el vector de dirección de r

 

Distancia de un punto a un plano

La distancia de un punto P a un plano es la distancia entre P y su proyección, P’, sobre el plano: d  (P, )  =  d (P, P’)

Al igual que en el caso anterior hay dos métodos, e primero se basa en calcular el punto P’ y el segundo, muy cómodo,  en usar esta fórmula:

Si  P(x_o, y_o , z_o)  y  : ax+by+cz+d=0     entonces:

 

  d (P, )=

 

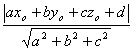
Distancia entre dos planos

Si los planos se cortan, la distancia ente ellos es cero. Si no se cortan es que son paralelos y entonces, si P es un punto de :   d (, ’)=d (P, ’)

 

 

Distancia de una recta a un plano

Si la recta y el plano se cortan, la distancia es cero.

Si no se cortan es porque la recta es paralela al plano entonces, si P es un punto cualquiera de r   d (r, ) =  d (P, )

 

Distancia entre dos rectas

Si las rectas r y s son paralelas se toma un punto de una y hallamos su distancia a la otra. Si P es un punto de r d (r, s)=  d (P, s)

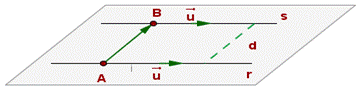
Si r y s se cruzan, para calcular la distancia entre ambas hay varios métodos para calcularla:

-Se halla el plano   paralelo a s que contiene a r.   Entonces   d (r, s)=  d (s, )= d (un punto de s, )

-Se calcula la perpendicular común a las dos rectas. La distancia entre los puntos de corte de dicha recta con r y s es la distancia entre ellas.  Es el más complejo.

-Otro método más fácil para hallar la distancia entre dos rectas que se cruzan se basa en la interpretación geométrica del producto mixto:

Si A y B son puntos cualesquiera de r y s, respectivamente:

                   

 

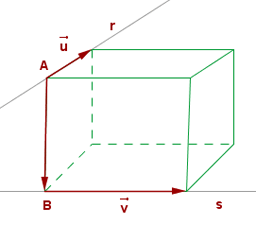
d  (r, s) == 

 

 

 

 

 

 

 

 

 

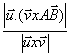
PARA  COMPLETAR EL TEMA IR A  EJERCICIOS DE GEOMETRÍA