Aplicación de la derivada a la representación gráfica de funciones

 

El conocimiento de una función se completa perfectamente dibujando su gráfica, los siguientes resultados dan una idea aproximada de ésta:

I) Estudio de f (resumen)

1º Dominio de f.

2º Puntos de corte con los ejes.

3º Signo de la función (regiones en las que varía el signo).

4º Simetrías.

- Si f(-x) = f(x), función par, simétricas respecto del eje de ordenadas.

- Si f(-x) =-f(x), función impar, simétrica respecto del origen.

5º Asíntotas

- Verticales

Si existe a tal que , x =a es la ecuación de una asíntota vertical.

- Horizontales

Si ,  y =b es una asíntota horizontal.

- Oblicuas

Si    y  , y =m x +n es una asuntota oblicua.

II) Estudio de f’ (resumen)

1º Crecimiento y decrecimiento.

Si f ’(x)>0 , f es creciente. Si f ’(x)<0, f es decreciente.

2º Máximos y mínimos relativos

Condición necesaria de máximo y mínimo es que f ’(x)=0.

III) Estudio de f’’(resumen)

1º Concavidad y convexidad, f ’’>0 convexaÈ, f ’’< 0 cóncava Ç

2º S i f ’’(x₀) =0 y en dicho punto cambia la curvatura es punto de inflexión.

 

EJERCICIOS MODELO

 

1.  Representación gráfica de

 

I) Estudio de f

-Dominio de f

Como f es una función racional, pertenecen al dominio son todos los números reales menos los q anulan al denominador, es decir:

D = R-

-Puntos de corte

a) Con el eje de las ordenadas, OY

Si x =0 entonces y = 0, luego pasa por (0, 0)

b) Con el eje de abscisas, OX

Si y =0 entonces , luego 2x=0, es decir x =0

Observa q da el punto (0, 0) de nuevo, esto quiere decir q la gráfica de f solo corta a los ejes en el origen de coordenadas.

- Signo de f (su estudio nos permite ver las regiones donde existe la gráfica y ayuda a posicionar las asíntotas)

Para estudiar el signo de f se señalan en la recta los puntos donde no hay función (es decir los q no pertenecen al dominio) y los puntos donde la función es 0, es decir

 

         -1                         0                          1                          

 

la recta queda dividida en 4 regiones donde puede cambiar el signo, basta tomar un punto en cada una de ellas para saber el signo de toda la región (esto mismo haremos para ver el signo de la derivada f’ y de la derivada segunda f’’)

 

f(-2)=, f(-1/2)=, f(1/2)<0, f(2)>0

 

     -            -1                +        0       -        1        +       

 

-Simetrías

La función es impar f(-x)==-f(x)

- Asíntotas

a) Verticales x=1, x=-1 (hay asíntotas en los puntos q no pertenecían al dominio)

b) Horizontales

luego y=0  es asíntota horizontal, y como la función es racional entonces no hay oblícuas.

II) Estudio de la derivada

- Monotonía

El signo de la derivada nos indica cuando la función crece (si f’ >0) y cuando la función decrece (si f’<0)

Los puntos en q la derivada es 0 son posibles puntos extremos (max o mín)

 y’=  (comprueba)

que como ves da siempre negativa en su dominio, por lo tanto podemos concluir:

a) decreciente en  R-

b) no tiene ni máximos ni mínimos locales

III) Estudio de la derivada segunda

Nos permite calcular los intervalos de concavidad y convexidad, así como los puntos de inflexión (condición necesaria q la derivada segunda valga 0)

 

y'’ =

Simplificando y agrupando queda:

y’’= = ,  si y’’=0 , x =0

Para estudiar la concavidad y convexidad y los puntos de inflexión estudiamos el signo de la derivada segunda:

f’’      -                           +                 -                 +

                   -1                0                 1                

 

 

                               

 

Como en el 0 cambia la concavidad f tiene ( en x=0) un punto de inflexión

 

La gráfica es: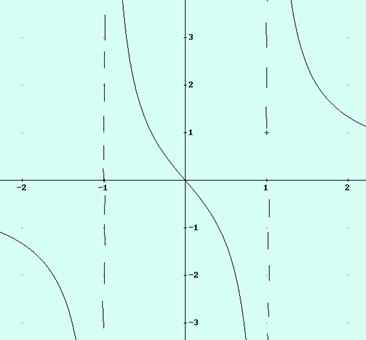                 

 

 

2. Representamos gráficamente la función

I) Estudio de f

1º D =R

2º Puntos de corte, el (0, 0)

3º Signo de f, negativa en x< 0 y positiva para x>0

4º Simetrías, f(-x) = -f(x), luego simétrica respecto del origen.

5º Asíntotas.

No hay verticales por que el dominio es todo R

Horizontales y =0

No hay oblicua.

II) Estudio de f ’

, f ’(x)=0 Þ -x²+1=0, de donde x =1

x	-		-1		1
f '(x)		-	0	+	0	-
f(x)		Decrece	Mínimo	Crece	Máximo	Decrece

 

 

 

 

 

 

 

1º f decrece en los intervalos ]-, -1[ y ]1, [  y crece en ]-1, 1[

2º Tiene un mínimo relativo en el punto (-1, -1/2) y un máximo relativo en el punto

(1, 1/2).

III) Estudio de f ’’

f ’’(x)==

f ’’(x)=0 Þ

x	-		-		0		+
f ’’		-	0	+	0	-	0
f		Ç	inflexión	È	inflexión	Ç	inflexión	È

 

 

 

En la tabla se indica la curvatura y los puntos de inflexión

La gráfica es:

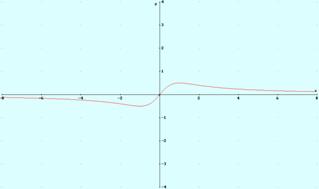
Ejercicios propuestos

1. Hacer el estudio y comprobar las gráficas:

a)

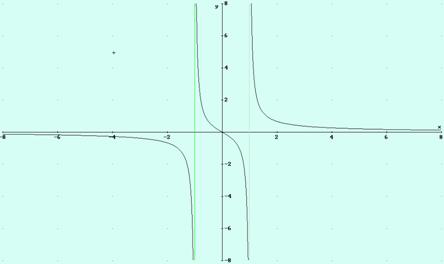
b)

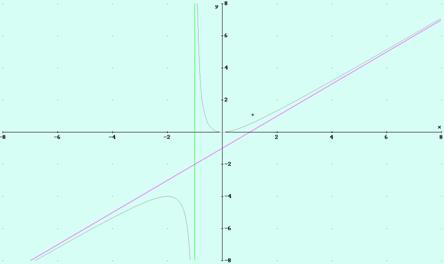
c)

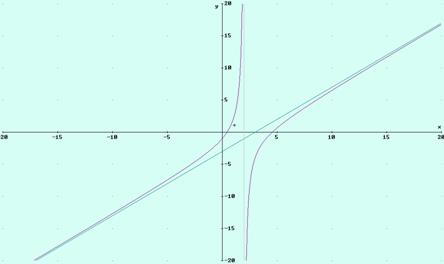
d) y = x³-3x²+2

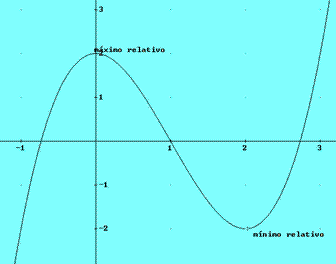
e) y = ln (x² -1)

 

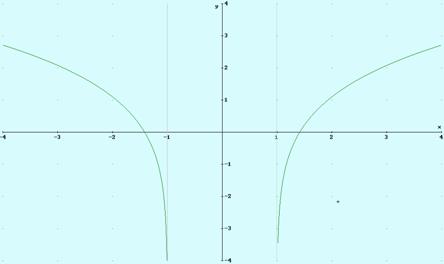
f) y = ln (x²+1)

 

 

Continúa                                                                                                                                          volver

Matemáticas en la Secundaria