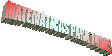REPRESENTACIÓN GRÁFICA DE FUNCIONES (continuación)
Una de las aplicaciones más importantes de la derivada es la representación gráfica de funciones.
EJEMPLOS RESUELTOS
1. Estudia y representa la función y= x3-3x2+2
I. Estudio de f
-Dominio. Todo R (f es un polinomio)
-Simetrías. No tiene
-Puntos de corte y signo de f (regiones de existencia de f)
Si x =0 entonces y=2, luego el punto de corte con el eje de ordenadas es (0, 2)
Si y =0, entonces x3-3x2+2=0, para encontrar las soluciones utilizamos la regla de Ruffini y llegamos a
 |
Una raíz es x =1, las otras las encontramos resolviendo la ecuación de 2º grado x2-2x-2=0
Cuyas
soluciones son x=
, simplificando nos queda: x= 
Los puntos de corte con el eje de abscisas son: (1, 0), (2’73, 0) y (-0’ 73, 0) y el signo:
-0,73 1 2,73
f - + - +
-Asíntotas no tiene.
II. Estudio de f ‘
- Crecimiento y decrecimiento. Extremos
y’ = 3x2 -6x , si y ‘ =0 entonces x = 0 y x = 2 f crece 0 decrece 2 crece
f ‘ + 0 - 0 +
De donde, además del crecimiento (crece de menos infinito a 0 y desde 2 a infinito) y decrecimiento (decrece de 0 a 2) de f, deducimos que en (0, 2) f tiene un máximo relativo y en (2, -2) tiene un mínimo relativo. No son absolutos pues f no está acotada ni superior ni inferiormente.
III. Estudio de f ‘ ’
-curvatura
y ´´ = 6x-6, si y ´´= 0 entonces x = 1 ,
f’’ - 0 +
f 
1
en
x =1 f tiene un punto de inflexión
La gráfica es:
2.
Estudia y representa 
I. Dominio
a) Si x + 1=0 entonces x =-1, por lo tanto D = R-{-1}
b) Simetrías no tiene
c) Puntos de corte y signo de f
(0, 0)
es el único punto de corte, y con ambos ejes.
Como el numerador es siempre positivo, el signo dependo solo de x+1, por lo tanto es negativa para x<-1 y positiva para x>-1
d) Asíntotas
La recta x =-1 es una asíntota vertical
Horizontales no tiene.
Como la diferencia de los grados del numerador y denominador es 1, tiene asíntota oblicua
m = 
; n = 
La asíntota tiene por ecuación y = x-1
II. Estudio de f’
- f’
(x)= 
,
Si f’(x)=0, x =0 y x = -2
f’ + 0 - infinito - 0 +
f crece -2 decrece -1 decrece crece
Además de los intervalos de crecimiento se deduce con este esquema q en x =-2 tiene un máximo relativo y en x =0 un mínimo relativo.
(encontrar sus ordenadas respectivas)
III. Estudio de la derivada segunda de f
-f’’
(x) =
=
=
Luego no se anula nunca, y por tanto no tiene puntos de inflexión
El signo de la derivada segunda depende solo del denominador, x+1, por lo tanto f’’ es negativa para x<-1 y f’’ positiva si x>-1
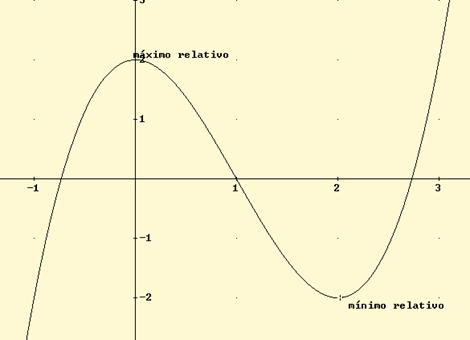
Con todos estos datos dibujamos la gráfica:
3.
Estudia y representa gráficamente la función 
I) Estudio de f
-Dominio
Si
x-1=0 
x
=1, luego D =R-
- Simetrías no tiene.
- Puntos de corte y signo de f
Corte con el eje de ordenadas, OY: si x =0, entonces y =0 pasa por (0, 0)
Cortes con el eje de ordenadas, OX: si y = 0, entonces x3=0, y por lo tanto x =0 (raíz triple), es decir el (0, 0) es el único punto de corte de la función con los ejes de coordenadas
Para encontrar el signo de la función señalamos en la recta el punto 0 y el 1 (ya q no pertenece al dominio de f)
x 0 1
f
+ 0 - 
+
(Esto nos da las regiones de existencia de f)
- Asíntotas
Tiene una asíntota vertical, la recta x =1
No tiene ni horizontales ni oblicuas
-No está acotada
II) Estudio de la derivada primera f’
f’(x)=
=
Para estudiar el crecimiento y los extremos igualamos a 0 la derivada
f ’(x)=0 de donde x2(2x-3)=0 cuyas raíces son x =0 y x = 3/2
Señalamos estos puntos en q la derivada es cero, y el 1, en una recta y estudiamos los intervalos de crecimiento viendo el signo de la derivada en dichos intervalos:
f’
- 0 - 1 - 3/2 +
f decrece decrece decrece crece
en el punto 3/2 la función tiene un mínimo relativo ya q, además de ser f’(3/2)=0, cambia el crecimiento (pasa de ser decrec a crec )
el punto es (3/2, 27/4)
III) Estudio de la derivada segunda
f’’(x)=
Para hallar la curvatura y los puntos de inflexión igualamos a 0 la derivada segunda,
2x(x2-3x+3)=0 que da como solución x =0
Señalando en la recta este punto y el 1, se llega a que en el 0 hay un punto de inflexión
f’’ + 0 - 1 +
f 
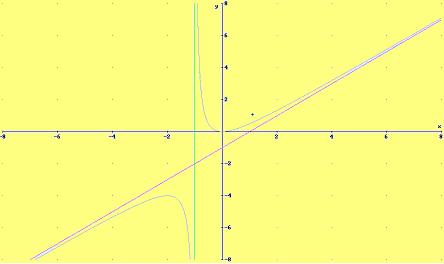
La gráfica es:
