II) LA DERIVADA
INTRODUCCIÓN
El deseo de medir y de cuantificar el cambio, la variación, condujo en el siglo XVII hasta la noción de derivada.
El estudio de las operaciones con derivadas, junto con las integrales, constituyen el cálculo infinitesimal. Los introductores fueron Newton y Leibnitz, de forma independiente. Los conceptos son difíciles y hasta bien entrado el siglo XIX no se simplificaron. A ello contribuyó la aparición de una buena notación, que es la que usaremos. Las aplicaciones prácticas de esta teoría no dejan de aparecer.
1. Tasa de variación media
Incremento de una función
Sea y = f(x) y a un punto del dominio de f. Suponemos que a aumenta en h, pasando al valor a +h, entonces f pasa a valer f(a +h), al valor h se le lama incremento de la variable, y a la diferencia entre f(a +h) y f(a) el incremento de la función.
Tasa de variación media
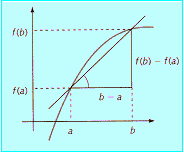Llamamos tasa de variación media (o tasa media de cambio) T.V.M.,
de la función y =f(x) en el intervalo [a, b] al cociente entre los incrementos
de la función y de la variable, es decir:
T.V.M. [a,
b] = 
Ejemplo 1. Halla la tasa de variación media de la función
f(x) =3-x2 en el intervalo [0,2]
Solución
T.V.M. [0, 2] = 
Ejercicio 1. Calcular b para que la tasa de variación media de la función f(x) = ln(x+b) en el intervalo [0,2] valga ln2.
2. Tasa de variación instantánea. La derivada
Consideremos un valor h (que puede ser positivo o negativo).
La tasa de variación media en el intervalo [a, a +h] sería 
.
Nos interesa medir la tasa instantánea, es decir el cambio cuando la h tiende a cero, es decir :
A este valor
se le llama la derivada de la función f en el punto a y se
designa por 
, por lo tanto, la derivada de
una función en un punto es el límite de la tasa de variación media cuando el
incremento de la variable tiende a 0.
=
Si f tiene derivada en el punto a se dice que f es derivable en a.
Observación 1. Si hacemos x =a +h , la derivada, en el punto a , también puede expresarse así:
Ejercicio 2. Hallar la derivada de la función f(x) = -x2 +4x el punto de abscisa x =1.
Observación 2. También se puede hablar de derivadas laterales, f ’+ y f -’ (obligatorio que f sea continua) según se considere el límite para h>0 o h<0. Si existen los dos límites laterales y coinciden la función es derivable.
Ejemplo 2. Las derivadas laterales de la función 
en
x =0 son 1 y –1.
Luego la función valor absoluto no es derivable en el 0.
Proposición. Toda. función derivable en un punto es continua en dicho punto.
El recíproco es falso.
Ejemplo
2. es continua en 0, pero no es derivable en 0.
Aplicación física de la derivada
Consideremos la función espacio E = E(t).
La tasa de variación media de la función espacio en el intervalo [t0, t] es:
:
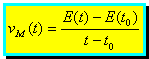
que es lo que en Física llaman la velocidad media en ese intervalo de tiempo, si calculamos el límite cuando t tiende a t0, obtenemos la tasa instantánea, entonces:
“La derivada del espacio respecto del tiempo es la velocidad instantánea”.
Ejercicio 3. La ecuación de un movimiento es , 
, calcula la velocidad en el instante t =5.
Solución
v(t)=E’(t)= 2t -6, en el instante t =5 se tendrá : v(5)= 2.5 -6 =4
3. Interpretación geométrica de la derivada
La tasa de variación media de una función f en [a, a +h] es la pendiente de la recta secante a la gráfica de f que pasa por los puntos de abscisa a y a +h.
Si h tiende a cero, el punto a +h tiende hacia el punto a y la recta secante pasa a ser la recta tangente a la curva. Por lo tanto:
La derivada de la función en el punto a es la pendiente de la recta tangente en el punto (a,.f(a))
La ecuación de la recta tangente en dicho punto se puede expresar
y - f(a) = f ´(a)(x-a) .
Ecuación punto pendiente de la recta tangente a la gráfica de f, pasa por el punto (a, f(a)) y tiene como pendiente la derivada de f en a, f’(a)
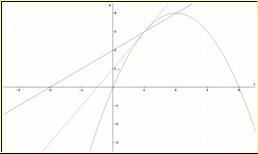Ejemplo 3. En la figura se muestra la gráfica de y =-x2
+4x, una recta secante que pasa por el punto (1, 3) y la recta tangente en ese
punto, que tiene por ecuación y –3 = 2(x-1)
Ejercicio 4. Hallar la ecuación de la recta tangente a la gráfica de f(x) = x2-x +5 en el punto de abscisa x=0
Ejercicio 5. ¿Qué valor debe tener a para que la recta y =-x +6 y la curva y =-ax2 +5x –1 sean paralelas en x = 1.
Indicación. Dos rectas son paralelas cuando tienen la misma pendiente
Nota. Para ver el tema de derivadas completo, a nivel de Bachillerato MCS, visita este enlace DERIVADAS Y SUS APLICACIONES