Cuaderno de actividades 1º

 

Nota: El tema también está  en formato pdf o se puede descargar el documento de Word

 

 Variables estadísticas bidimensionales.

En numerosas ocasiones interesa estudiar simultáneamente dos (o más) caracteres de una población. En el caso de dos (o más) variables estudiadas conjuntamente se habla de variable bidimensional  (multidimensional );  si se trata de dos caracteres cualitativos, de par de atributos.

Si de una cierta población se estudian dos caracteres simultáneamente se obtienen dos series de datos.

 

La lista de pares de datos correspondientes a cada individuo de la población (repetidos o no), es lo que llamamos variable estadística bidimensional.

Ejemplo 1. A cada uno de los reclutas de un reemplazo se les talla y pesa. Se trata de dos variables cuantitativas.

 

xi  ( tallas en m )	1,70	1,69	1,68	1,70	........
yi  ( peso en kg )	75	70	66	67	.........

 

Ejemplo 2. Entre los empleados de una empresa se ha realizado una encuesta sobre el consumo del tabaco, que ha arrojado los siguientes resultados:

 

Hábito Sexo	Fumadores	No fumadores	Totales de filas
Varones Mujeres	49     43	64        37	113      80
Totales de columnas	92	101	Total general  193

 

Nota. En este tema nos limitaremos al estudio de caracteres cuantitativos discretos, puesto que si el carácter es continúo o discreto agrupado en intervalos, se trabajará con las marcas de clase.

 

2. Distribuciones de frecuencias.

Se disponen las frecuencias en una tabla de doble entrada donde las x_i  y la y_j están ordenadas en forma creciente. Recibe el nombre de tabla de frecuencias o tabla de correlación.

Si hay  pares que se repiten se agrupan siendo n_ij la frecuencia absoluta del par (x_i, y_j).

Las sumas:

 

ån_ij = n_i , frecuencia absoluta de x_i.

 ^j

ån_ij = n’_j , frecuencia absoluta de y_j

    ⁱ    

se llaman frecuencias absolutas marginales de las variables X e Y respectivamente.

åån_ij = N = número total de pares.

 ^{j  i}

X     Y	x1	x2	.......	xk	Frec. absolutas marginales de Y
y1	n11	n21	.....	nk1	n’1
y2	n12	n22	......	nk2	n’2
......	.....	....	....	...	.... .
yr	n1r	n2r	...	nkr	n’r
Frec. absolutas marginales de X	n1	n2	..	nk	åånij = N             i  j

 

En la práctica algunas de las n_ij puede ser cero. En tal caso la casilla correspondiente se dejará en blanco.

Ejemplo 3. Dada la distribución bidimensional:

 

X	1	2	1	2	3	2	2	2	3	1
Y	3	5	2	3	5	4	3	5	5	3

 

la tabla correspondiente es:

 

X     Y	1	2	3	Frec. absolutas marginales de y
2	1			1
3	2	2		4
4		1		1
5		2	2	4
Frec. absolutas marginales de X	3	5	2	N=10

 

u Al estudiar una variable bidimensional se obtienen varias distribuciones unidimensionales, según se consideren las filas o las columnas de la tabla en estudio. 

Las distribuciones unidimensionales del total de los individuos de la población, respecto a cada una de las características reciben el nombre de distribuciones marginales.

Distribución marginal de la Y:

 

Y	Frec. absolutas marginales de Y
y1 y2 . . yr	n’1 n’2 . . n’r

 

Análogamente la distribución marginal de la X

Ejemplo 4.

Obtener  la distribución marginal de la variable X.

X	Frec. absolutas marginal de X
1 2 3	3 5 2

 

u Si en la tabla de correlación consideramos la primera columna y una columna intermedia , la correspondiente a y_j, se obtiene una distribución unidimensional que llamaremos distribución condicionada de la variable X por la modalidad y_j de la variable Y.

 

X	Frec. absolutas condicionadas por yj
x1 x2 . . xk	n1j n2j . . nkj

 

 Análogamente se define la distribución condicionada de la variable Y por la modalidad x_i  de la variable X.

Ejemplo 5.

Obtener la tabla de la distribución condicionada de la variable Y por la modalidad x₂.

 

Y	Frec. absolutas condicionadas por x2
2 3 4 5	0 2 1 2

 

 

3. Representaciones gráficas.

Consideremos la distribución:

x1	x2	.....	xN
y1	y2	.......	yN

 

( Los  pares pueden estar repetidos )

Los pares de valores observados (x_i , y_j) se pueden representar en unos ejes de coordenadas,.

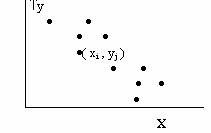                                                    x ^®

El conjunto de puntos que resulta se llama diagrama de dispersión o nube de puntos de la distribución bidimensional.

Cuando  el número de datos es grande (se usa una tabla de doble entrada) los datos se representan con un diagrama de dispersión reticulado de tal manera que la visión de la nube de puntos indique realmente cómo es la distribución.

En estos casos también se suele usar un diagrama de barras sobre un sistema cartesiano de tres dimensiones (estereogramas).

Ejemplo 6.

Hacer el diagrama de dispersión de la distribución del ejemplo 3. 

Ejercicio 1. Dibuja el estereograma correspondiente .

 

4. Parámetros de la variable estadística bidimensional.

 

 

Considerando las distribuciones marginales, como son unidimensionales es posible calcular los siguiente parámetros:

Llamadas medias marginales.

Nota. En una distribución bidimensional al punto (x, y ) se le llama centro de gravedad de la distribución.

b) Varianzas

Se define:

(Es decir la “media del cuadrado menos el cuadrado de la media”)

Análogamente la varianza marginal de la variable Y. De ellas  (extrayendo la raíz cuadrada ) se obtienen las correspondientes desviaciones típicas.

Ejemplo 7. Calcula las medias marginales y las Varianzas de la v.e.del ejemplo 3.

Solución  x = 19/10=1,9 ; y =38/10= 3,8 ; Sx2= 4,1-(1,9)2= 0,49 ; Sy2= 15,6 - 14,44=1.16.

 c) Covarianza

Para las variables estadísticas bidimensionales se define la  “ covarianza ’’ como la media aritmética de los productos de las desviaciones respecto de la media de cada una de las variables componentes.

Es decir:

Se demuestra que

 

propiedad que facilita el cálculo de la covarianza. (Ver problema resuelto 2)

Ejempl 8.   Calcula la covarianza de la distribución del ejemplo 3.

Solución :

Sxy =   - (1,9)·(3,8) = 0,58.

 

4. Regresión lineal.

Al considerar los dos caracteres de una variable bidimensional  puede ocurrir.

Y Que exista una dependencia funcional entre ellos, de tal manera que a cada valor le corresponda un único valor del otro. Ejemplo: la temperatura a la que calentamos una barra de hierro y la longitud alcanzada.

Y Que haya una dependencia estadística o correlativa, de tal manera que los valores sigan unas pautas similares. Por ejemplo el número de horas de estudio y las notas obtenidas.

Y Que se de una independencia entre los caracteres. Por ejemplo la estatura y las calificaciones en Matemáticas.

El estudio de la relación entre dos caracteres de una variable estadística bidimensional es el objeto de la regresión lineal.

La nube de puntos de una distribución bidimensional nos da una primera idea de la relación existente entre los datos de la misma.

Cuando la nube de puntos del diagrama de dispersión permita deducir algún tipo de dependencia entre las dos variables X, Y, concentrándose los puntos alrededor de una cierta línea (línea de regresión) se plantean dos cuestiones:

A) Definir la línea.

B)  Medir el nivel de aproximación de dicha línea.

Sí la línea es una recta  , el problema es un caso típico de regresión lineal.

A) Rectas de regresión.

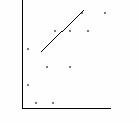
Se llama recta de regresión a aquella que mejor se ajusta a la nube de puntos.

El procedimiento más usado, para hallar dicha recta, es el los mínimos cuadrados.

Se calcula la recta :

y = ax + b,        de tal manera que :

S=å [y_i - (a x_i + b )]²            sea mínima

El cálculo de a y b  incluye conocimientos que no se dan en este nivel^[1] por lo que sólo daremos el resultado:

Se verifica:

a= ^{Sxy                  b= y - Sxy   x}        

     ^{Sx2                                    Sx2}

 

luego se puede escribir :

y=  ^{Sxy    x  +  y - Sxy   x     o lo que es igual:   y - y = Sxy   ( x - x )  .}

      ^{Sx2                   Sx2                                                                               Sx2}

Esta es la ecuación de la recta de regresión de Y sobre X.  Sirve para hacer estimaciones  o predicciones de los valores de Y conocidos los de X.

Análogamente  la recta de regresión de X sobre Y tiene por ecuación:

^{x - x = Sxy  (y - y )}

                 ^Sy2

A  m_yx =  ^Sxy            y      m _xy  ^{=    Sxy}          se les llama los coeficientes de regresión

                    ^{Sx2                                             Sy2}

Ejemplo 10.   Hallar las rectas de regresión para la distribución del ejemplo 3.

Solución:  recta de regresión de Y sobre X      y - 3,8 = 1,18 (x- 1,9)

                 recta de regresión de  X  sobre Y     x - 1,9 = 0,5 ( y - 3,8 ).

Nota. Daremos sin demostración algunas propiedades del coeficiente de regresión que facilitan los cálculos de estos, pues permiten hacer un cambio de variable.

Propiedades del coeficiente de regresión:

1) Si se suma o resta una constante a todos los valores de X o de Y el coeficiente de regresión myx   no varía.

2) Si se multiplican todos los valores de X por una constante, el coeficiente de regresión queda dividido por esa constante.

Si se multiplican todos los valores de y por una constante, el coeficiente de regresión m_yx  queda multiplicado por es constante.

Ejemplo 11.  Consideramos la tabla:

 

1980	430000
1983	450000
1986	475000
1989	500000

 

Si hacemos  X’= ,  Y’ =

Se obtiene:

0	-20
1	0
2	25
3	50

 

Para la variable X’ ,Y’ es más fácil el cálculo del coeficiente de regresión y la relación entre éste y el de XY es:

m’yx  = 

B) Correlación lineal.

Se entiende por correlación la dependencia que existe entre las variables de una distribución., cuando ésta es, en cierta forma, lineal se habla de correlación lineal.  Cuando  no existe tal dependencia se dice que las variables están incorreladas.

Para medir, de una forma cuantitativa, dicha dependencia se utiliza el llamado coeficiente de correlación lineal, o de Pearson, que se define así:

^{r =}

El signo es +  si  la covarianza es positiva y  - si es negativa..

Propiedades de r

a) -1r 1

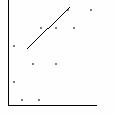
b) Si r es positivo la correlación es directa, es decir, al aumentar una variable también aumenta la otra (coeficiente de regresión positivo). En este caso las pendientes de las rectas de regresión son positivas.

. .	.   . .  .
.  .   .  .	.

 

Si r es negativo la correlación es inversa, es decir, al aumentar una variable disminuye la otra. En este caso las pendientes de la rectas de regresión son negativas.

c) Si r² = 1, es decir, r igual a 1 o a -1, las dos rectas de regresión coinciden y la nube de puntos está contenida en la recta (correlación perfecta). Hay dependencia funcional entre las variables.         

d) Si r = 0  las rectas de regresión son perpendiculares entre sí y paralelas a los ejes. Las variables  son incorreladas.

 

 

Para los demás valores de r la dependencia es tanto más fuerte cuanto más próximo esté a 1 o a -1. Será más débil cuando se aproxime a 0:

Para la correlación directa:

 Si    0,75£  r £ 1 correlación muy alta.

Si     0,40 £  r £ 0,75  correlación  baja

Si      r < 0,40    la correlación es casi despreciable .

Ejemplo 12.  Hallar el coeficiente de correlación lineal para la distribución del ejemplo 3.

Solución :  r =+= 0,76.  Se trata de una correlación directa alta.

Problemas resueltos

1. Una asociación dedicada  a la protección de la infancia decide estudiar la relación entre la mortalidad infantil en cada país y el número de camas de hospitales por cada mil habitantes.. Datos

x	50	100	70	60	120	180	200	250	30	90
y	5	2	2,5	3,75	4	1	1,25	0,75	7	3

 

Donde x es el nº de camas por mil habitantes e y el tanto por ciento de mortalidad.

Se pide calcular las rectas de regresión y el coeficiente de correlación lineal.

¿ Si se dispusiese de 175 camas por mil habitantes que tanto por ciento de mortalidad cabria esperar?. ¿La estimación es fiable? Razona la respuesta.

Solución :

Para facilitar los cálculos de los parámetros se utiliza la siguiente tabla:

 

	xi	yi	xi2	yi2	x i yi
	50	5	2500	25	250
	100	2	10000	4	200
	70	2,5	4900	6,25	170
	60	3,75	3600	14,0625	225
	120	4	14400	16	480
	180	1	32400	1	180
	200	1,25	40000	1,5625	250
	250	0,75	62500	0,5625	187,5
	30	7	900	49	210
	90	3	8100	9	270
å =	1150	30,25	179300	126,4375	2422,5

 

x =115;   y= 3,025%;   S_x =68,59;  S_y== 1,87  ; S_xy== -105,625

Las rectas de regresión serán por tanto:

y - 3,025 = -0,022449 (x - 115)

x - 115  =  -30,2053 ( y - 3,025)

El coeficiente de correlación lineal:

r=  = - 0,8235

es una correlación inversa alta .

Para la estimación que nos piden utilizaremos la recta de regresión de Y sobre X.

y= 3,025 - 0,022449(175- 115) = 1,6783 que sería fiable por ser alto el coeficiente de correlación.

2. Dada la distribución bidimensional:

 

X	1	2	1	2	3	2	2	2	3	1
Y	3	5	2	3	5	4	3	5	5	3

Encuentra el valor del coeficiente de correlación lineal usando una tabla de correlación.

Solución

Se usa la siguiente tabla de doble entrada que facilita los cálculos:

X       Y	1	2	3	n’j	nj’yj	n’jyj2	nijxiyj
2	1			1	2	4	2
3	2	2		4	12	36	18
4		1		1	4	16	8
5		2	2	4	20	100	50
ni	3	5	2	10	å=38	å=156	å=78
nixi	3	10	6	å=19
nixi2	3	20	18	å=41
nijxiyj	7	40	30	å=78

           

De aquí se tiene:

x = 19/10= 1,9; y = 38/10= 3,8;  S_x²= 4,1 - (1,9)²= 0,49,   S_x =0,7 ; S_y²=15,6 - (3,8)²= 1,16,

S_y = 1,077; S_xy = 7,8 - (1,9)(3,8)= 0,58.

Luego    r =  =  0,769

3^[2]. En la tabla siguiente se dan los valores y algunas frecuencias absolutas de un par de variables tratadas conjuntamente. Los valores de la primera fila corresponden a la variable Y, y los de la primera columna a la variable X. La última columna es la marginal de X y la última fila es la marginal de Y.

 

	1	2	4	7	9	11
1	1	2		1	0	0	5
3	0			1	1	0	4
4	1	0	2	1	1	3
5	1	1	3	2	4	0
6		1	1		1	0	4
7	0	0	0	1	3	1
	4	5	8	6	10	4

a) Completar la tabla.

b) Calcular el coeficiente de correlación y las rectas de regresión.

c) ¿Sirven las rectas de regresión para hacer predicciones de una variable en función de la otra? ¿Por qué?

Solución

 

x            y	1	2	4	7	9	11
1	1	2	1	1	0	0	5
3	0	1	1	1	1	0	4
4	1	0	2	1	1	3	8
5	1	1	3	2	4	0	11
6	1	1	1	0	1	0	4
7	0	0	0	1	3	1	5
	4	5	8	6	10	4	37

 

b) x = ;  y = = 6

M_xy ^[3] =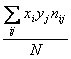= 28,378, luego  S_xy = M_xy - x.y = 1,948

S_x² = ;  S_x=1,764

 

S_y² = 47,027 - 36 = 11,027;   S_y = 3,321

 

 

El coeficiente de correlación lineal r = = 0,3325 <0,40, correlación baja.

 

m_yx = 1,948/3,11=0,626  y   m_xy = 1,948/11,027=0,177     son los coeficientes de regresión.

 

Las rectas de regresión son:

y - 6 = 0,626 (x - 4,405)   de Y sobre X,  y   x - 4,405 = 0,177(y - 6) de X sobre y

c) Las rectas de regresión no sirven para hacer predicciones, fiables, de una variable respecto de la otra ya que la correlación es baja. (El módulo del coeficiente de correlación lineal está muy alejado de la unidad)

 

 

Problemas propuestos

1. Las tallas y los pesos de 10 personas vienen recogidos en la siguiente tabla:

talla (cm)	160	165	170	180	185	190	192	175	182	172
pesos (kg)	58	61	65	73	80	85	83	68	74	67

 

Estimar el peso medio de una persona que mida 168 cm.

2. El número de licencias de caza, en miles, y el número de votantes a un determinado partido en 6 comunidades autónomas, en decenas de miles, está expresado en la siguiente tabla.:

Nº de licencias (X)	103	26	3	7	26	5
Nº de votantes (Y)	206	26	27	14	24	12

Determinar:

1) Media y varianza de las variables X e Y.

2) Coeficiente de correlación, interpretando su valor.

3) En el caso de que exista correlación: si en una determinada comunidad existen 50 decenas de millar de votantes, ¿cuántas licencias de caza, en miles, se puede estimar que existen.

3.  Las distancias medias de los 19 planetas al Sol son:

1. Merc	2. Ven.	3. Tie.	4. Ma.	5. Ast.	6. Jup.	7. Sat.	8. Ur.	9. Nep.	10. Plu
0,39	0,72	1	1,52	2,65	5,2	9,54	19,19	30,07	39,52

 

(Se ha tomado como unidad la distancia entre la Tierra y el Sol, a lo que se llama unidad astronómica (u.a.). El quinto lugar está ocupado por los asteroides que, para estos efectos, son considerados como un planeta más.)

Representa la nube de puntos correspondiente, traza la recta de regresión y calcula el coeficiente de correlación. Si hubiera un nuevo planeta más allá de Plutón, ¿a qué distancia en u.a. estaría del Sol?. ¿Sería “fiable” esta medida?

4. Observaciones realizadas con estudiantes de Matemáticas, sobre el efecto del paso del tiempo en los conocimientos adquiridos, arrojan los siguientes resultados:

1 día .....................   90 % de permanencia de conocimientos.

2 días ....................  75 %          “                      “

3 días ....................  42 %          “                      “

4 días ....................  30 %          “                      “

5 días ....................  21 %           “                      “

Tomando los días transcurridos (X) y el tanto por ciento (Y) como variables de una distribución dimensional, halla la recta de regresión de Y sobre X y estima, si existe una correlación fuerte, el tanto por ciento de conocimientos que permanecerán a los ocho días. Organiza los cálculos y explica el resultado.

 

 

Todos los temas de Estadística los encontrarás en esta dirección Elementos de probabilidad y Estadística

 

 

Matemáticas en la secundaria