Continuación

5. Crecimiento y decrecimiento de una función

Proposición. Si una función f es derivable en un punto a, y f’(a)>0 entonces f es creciente en el punto a.

 

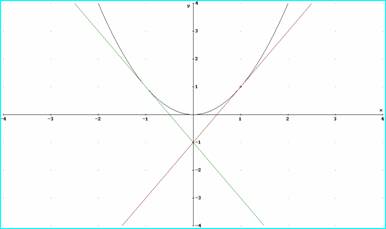
Figura 1

 

La demostración de este resultado puede hacerse usando la definición de derivada y e concepto de límite, pero resulta evidente si se tiene en cuenta el significado geométrico de la derivada (ver figura 1).

Si f es derivable en un intervalo I y f ’ >0  en ese intervalo entonces f crece en I.

El recíproco no se cumple en general.

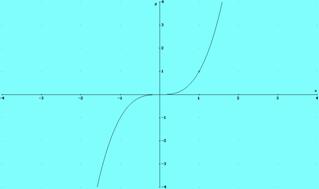
Ejemplo 5. La función y =x³ cumple que es creciente en todo R, y sin embargo f ’(0) =0.

Análogamente si f es derivable en un punto a y f ‘(a)<0 entonces f es decreciente en a. Si f ‘<0 en todo un intervalo I, f es decreciente en I. (Ver figura 1)

6. Máximos y mínimos relativos (o locales) de funciones derivables

Si una función tiene un máximo o mínimo relativo (o local) se dirá que tiene un extremo relativo.

Figura 2

Condición necesaria de extremo

Proposición. Si f es derivable en el punto a y f tiene en a un extremo relativo, entonces f ‘ (a)=0.

Demostración. Si no fuera cierto y por ejemplo f ’(a)>0 entonces por la proposición anterior f sería creciente en un entorno del punto a, lo que contradice la existencia de extremo.

La condición no es suficiente.

Ejemplo 6. La función y =x³ es creciente en 0, por lo que no puede tener extremos, y sin embargo f ’(0)=0.

Criterio práctico. Hay extremo relativo en el punto si la derivada de la función en ese punto es cero (condición necesaria f ‘(0)=0) y en dicho punto cambia el crecimiento. Ver figura 2.

         f ’      <0      =0               >0     

Si                         |a                       hay mínimo relativo en (a, f(a))

             f                      mínimo         

 

f ’      >        0                 <                 

Si                         |a                       hay máximo relativo en (a, f(a))

                   f                 máximo       

Ejercicio 9.Dada la función  se pide estudiar el crecimiento y decrecimiento, máximos y mínimos relativos.

Condición suficiente de extremo

Proposición. Sea f una función derivable en a y tal que f ‘(a)=0:

a) Si f ’’>0 entonces f tiene un mínimo relativo en el punto a.

b) Si f ‘’<0 entonces f tiene un máximo relativo en el punto a.

Esta proposición nos da también un método para resolver los problemas de máximos y mínimos para funciones derivables.

Se presentarán en  tablas estos resultados:

 

f(x)	Crece	Máximo	Decrece
f '(x)	+	0	-
f ''(x)	-	-	-

 

 

 

 

 

f(x)	Decrece	Mínimo	Crece
f '(x)	+	0	-
f ''(x)	-	-	-

 

 

 

 

 

Ejercicio 10. Descomponer un número N en dos sumandos x e y de tal manera que  sea mínimo.

Nota[1]. Cuando busquemos los extremos absolutos de la función f, si esta es continua en un cerrado y derivable en el abierto, buscaremos los valores en que la derivada es cero y los compararemos con los de los extremos, el valor mas grande será el máximo y el más pequeño el mínimo.

Ejercicio 11. Se considera la función f(x) =x³ –3x definida sobre el intervalo [-2,2], se pide hallar los puntos donde f alcanza máximo absoluto.

Ejercicio 12. Entre todos los rectángulos de 20cm de perímetro halla el que tiene diagonal mínima.

7. Algunas “precisiones” sobre los extremos de funciones

OBSERVACIÓN 1. Decir que f posee un máximo local en un punto x₀, significa que existe un intervalo (x₀ - r, x₀ + r) tal que f(x)f(x₀) para todo x perteneciente al conjunto  (x₀ - r, x₀ + r) Ç D_{f .}

Análogamente para mínimo local.

Esta matización en la definición de extremo, de intersecar el entorno con el  dominio de f, D_f,  es esencial. En otro caso se puede llegar al absurdo de decir que una función continua, definida en un dominio compacto no tiene extremos locales (cuando sabemos por el teorema de Weiertrars que los posee incluso absolutos), cuando éstos se alcanzasen en puntos no interiores del dominio.

OBSERVACIÓN 2. No se deben asociar tanto los extremos locales a las derivadas, ya que éstos pueden encontrarse en los puntos en que la función no es derivable.

Ejercicio 13. La función:

(su dominio es [-2,3])

 

Cuya gráfica se adjunta

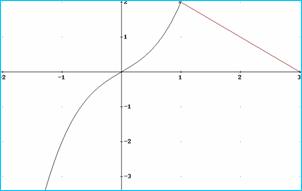
_{Figura 3}

¿Tiene extremos locales? ¿tiene extremos absolutos?. En caso afirmativo ¿en qué puntos se alcanzan?. Razonas la respuestas.

Si no tuvieras las gráficas ¿cómo les localizarías?

Teniendo expuesto anteriormente deduce razonadamente como se pueden calcular los extremos (absolutos y relativos) de una función.

Ejercicio 14. Calcula los extremos (indica si son absolutos o no) de las siguientes funciones, en caso de que existan:

a) f(x)=-x³ +3x;      b) ;  c)

d)

e)

Problemas resueltos de máximos y mínimos de funciones derivables (pincha aquí)

8. Concavidad y convexidad. Puntos de inflexión

Una función es convexa[2] en a, si existe un intervalo que contiene al punto a,  tal que la diferencia entre la ordenada de la función y la ordenada de la tangente a la gráfica de f en el punto (a, f(a)) es positiva en dicho intervalo.

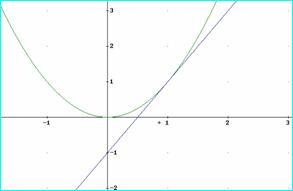
Figura4

Análogamente se dice que es cóncava cuando dicha diferencia es negativa.

Se dice que f tiene un punto de inflexión en a si existe un entorno de a en que la diferencia entre la ordenada de f y la de la tangente en a tiene distinto signo a la izquierda que a la derecha.

Por lo tanto f tiene un punto de inflexión en a si en dicho punto la tangente atraviesa a la gráfica.

 

 

 

Ejemplo 7. En la gráfica aparece la función y = x³ y la tangente en el punto x =0. Se aprecia que en dicho punto la gráfica posee una inflexión.

 

 

               Figura 5

Proposición. Si la función es derivable en a y f’’(a)>0 se verifica que f es convexa en a.

Análogamente si f es derivable en a y f’’(a)<0 se verifica que f es cóncava en a.

Criterio práctico. Para calcular los puntos de inflexión se halla la derivada segunda de f, se igual a cero y se resuelve la ecuación. En las soluciones de la ecuación se estudia y si cambia la curvatura hay punto de inflexión.

f ’’(x)	+	0	-
f (x)	Convexa È	P.inf	Cóncava Ç

 

 

 

 

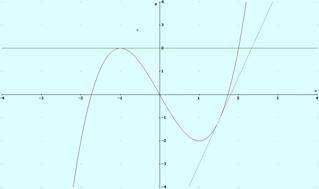
Ejemplo 8. En la gráfica de la figura se aprecia que la función es cóncava en el punto –1 es convexa en el punto 3/2 y tiene un punto de inflexión en el 0:

 

Ejercicio 15. Dada la función  estudia la curvatura y los puntos de inflexión.

 

9. Aplicación de la derivada a la representación gráfica de funciones (en este link)

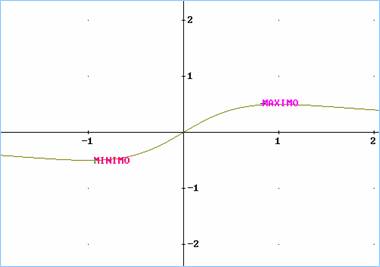
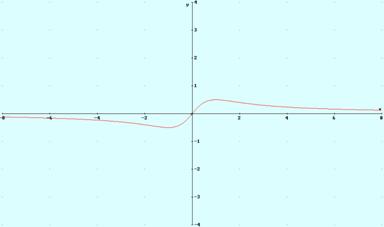
Ejemplo 8. Representamos gráficamente la función

I) Estudio de f

1º D =R

2º Puntos de corte, el (0, 0)

3º Signo de f, negativa en x<0 y positiva para x>0

4º Simetrías, f(-x) = -f(x), luego simétrica respecto del origen.

5º Asuntotas.

No hay verticales por que el dominio es todo R

Horizontales y =0

No hay oblicua.

II) Estudio de f ’

,           f ’(x)=0 Þ -x²+1=0, de donde x =1

-		-1		1
f '(x)	-	0	+	0	-
f(x)	Decrece	Mínimo	Crece	Máximo	Decrece

 

 

 

 

1º f decrece en los intervalos ]-, -1[ y ]1, [  y crece en ]-1, 1[

2º Tiene un mínimo relativo en el punto (-1, -1/2) y un máximo relativo en el punto

(1, 1/2).

III) Estudio de f ’’

f ’’(x)==

f ’’(x)=0 Þ

 

-		-		0		+
f ’’	-	0	+	0	-	0
f	Ç	inflexión	È	inflexión	Ç	inflexión	È

En la tabla se indica la curvatura y los puntos de inflexión

La gráfica es:

Ejercicio 16. Representar las gráficas de las siguientes funciones:

a) ; b) ; c)

 

Ejemplo 9. La gráfica de y = ln (x²+1) es:

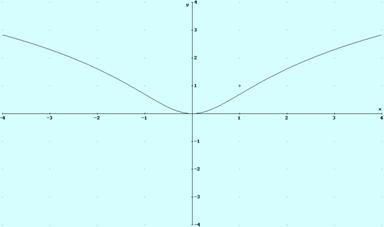
Ejemplo 10. La gráfica de y =ln (x²-1)

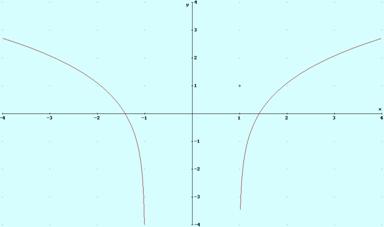
Ejercicio 17. Representa gráficamente: a) y = x e ^x; b) .

Si necesitas ejercicios o problemas del tema visita las siguientes páginas:

Representación gráfica                                                   Aplicaciones al cálculo de máximos y mínimos

 

Matemáticas en el Bachillerato