APLICACIONES DE LAS DERIVADAS A LA RESOLUCIÓN DE PROBLEMAS:

MONOTONIA (CRECIMIENTO Y DECRECIMIENTO) Y  OPTIMIZACIÓN (MÁXIMOS Y MÍNIMOS)

 

EJERCICIOS RESUELTOS

 

1. Un fondo de inversión genera una rentabilidad que depende de la cantidad de dinero invertida, según la formula: R(x)=-0.002x²+0.8x-5 donde R(x) representa la rentabilidad generada cuando se invierte la cantidad x. Determinar, teniendo en cuenta que disponemos de 500 euros:

a) Cuando aumenta y cuando disminuye la rentabilidad

b) Cuanto dinero debemos invertir para obtener la máxima rentabilidad posible.

c) Cual será el valor de dicha rentabilidad.

Solución

a) La derivada primera nos da el crecimiento o decrecimiento de la función. Si la derivada es positiva la función crece y si es negativa decrece

Procedimiento:

-Se deriva la función:

R`(x)=-0,004x+0,8

-Se iguala a 0 y se resuelve la ecuación que resulta:

R`(x)=0 ,

 

-Se estudia el signo de la derivada a la derecha e izquierda de los valores que nos ha dado 0 la derivada (en este caso x =200). Hay varios métodos, uno muy mecánico:

                   f

                   f ´               +       200    -

se coge un punto menor que 200, por ejemplo 100, y sustituimos R´(100)=0,4>0 y en otro mayor que 200 (por ejemplo 300) R´(300)=-0,4<0

 

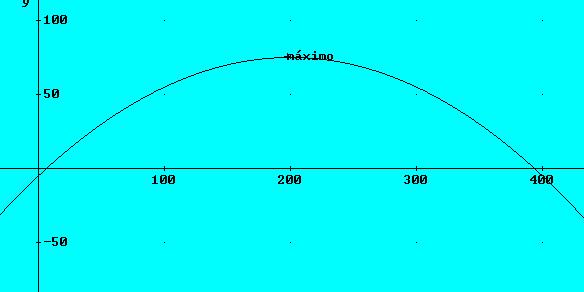
Entonces la derivada es positiva en el intervalo (0, 200), y f es creciente en ese intervalo y es decreciente en (200, 500) ya que en ese intervalo nos ha dado negativa la derivada. Lo que nos dice también que en punto 200 hay un máximo local

b) Teniendo en cuenta el apartado a debemos invertir 200 euros.

c) La máxima rentabilidad es R(200)= -0,002.(200)²+0,8.200-5=75 euros

Solución gráfica

 

5. La virulencia de cierta bacteria se mide en una escala de 0 a 50 y viene expresada por la función V(t)= 40+15t-9t²+t³, donde t es el tiempo(en horas) transcurrido desde que comienzo en estudio (t=0). Indicar los instantes de máxima y mínima virulencia en las 6 primeras horas  y los intervalos en que esta crece y decrece.

Solución

Para que la función  tenga un máximo o un mínimo la derivada debe ser cero.

 V´(t)= 15-18t+3t², igualando a 0, 3t²-18t+15=0

Simplificando  t²-6t+5=0, cuyas soluciones son 5 y 1.

Ahora voy a ver  quien  es el máximo y quien el mínimo de la función, en el intervalo [0, 6], que tiene que estar entre estos dos valores junto o en los extremos del intervalo (por el teorema de Weirtrars).

Ordenamos la función V por comodidad, V(t)= t³-9t²+15t+40

V(0)=40

V(5)=125-225+75+40 =15

V(1)=1-9+15+40= 47

V(6)=216-324+90+40=22

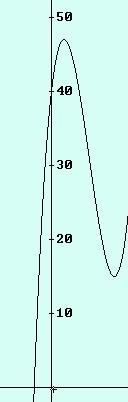
La máxima virulencia es a las 1 horas y la mínima a las 5 horas.

Para ver los intervalos de crecimiento y decrecimiento estudiamos el signo de la derivada: V’(t)=3t²-18t+15

     0        1                       5             6        

V’        +    0          -        0        +

Luego V crece desde 0 a 1  y desde 5 a 6, (crece en  (0, 1) unión (5, 6) ) y decrece en el intervalo (1, 5)

 

Observando la gráfica de esta función vemos lo q hemos deducido.

 

6. Un coche de competición se desplaza a una velocidad que, entre las 0 y 2 horas, viene dada por la expresión v(x)= (2-x).e^x, donde x es el tiempo en horas y v(x) es a velocidad en cientos de kilómetros. Hallar en que momento del intervalo circula a la velocidad máxima y calcular dicha velocidad. ¿En que periodos gano velocidad y en cuales redujo? ¿Se detuvo alguna vez?

SOLUCIÓN

Nos piden q estudiemos el crecimiento y decrecimiento y el máximo de la función velocidad v.

Por eso utilizamos la derivada, ya que sabemos (por teoría) que si la derivada da positiva la función crece y si da negativa decrece. También sabemos que, la función tiene un máximo relativo en un punto, si la derivada, en ese punto, es 0 (condición necesaria) y además cambia el crecimiento (es decir pasa de crecer a decrecer)

La derivada es:

v’(x)=-1.e^x + e^x.(2-x)= -e^x + 2 e^x- x .e^x = e^x- x. e^x, sacando factor común  e^x se llega a: v’(x)=((1-x)e^x

Igualando a 0 nos  da (1-x).e^x =0, de donde 1-x =0 y por tanto  x =1, (ya q e^x nunca puede ser cero)

Estudiamos v en los alrededores de 1

 

v ‘      +        1        -        2

y        crece           decrece

 

Por lo tanto en x=1 hay máximo y la función crece de 0 a 1 (gana velocidad) y decrece de 1 a 2 (reduce velocidad), veamos los valores en ese punto y en el extremo:

v(x)= (2-x)e^x

v(1)=(2-1).e = e (aquí el máximo como justificamos antes)

v(0)=(2-0).1=2

v(2)=(2-2).1=0       como da la velocidad  0 aquí se detuvo.

 

LA GRÁFICA:

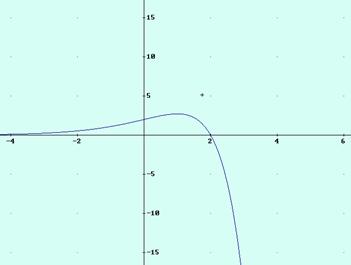
(No es necesaria la gráfica solo la pongo para ayudar a entender lo que se hace, vemos que pasa justo lo que hemos deducido entre 0 y 2)

7. La cantidad de agua recogida en 2002 (en millones de litros), en cierto pantano, como función del instante de tiempo t (en meses), viene dada a través de la expresión

 

 Se pide:

a)  En que periodo de tiempo aumento la cantidad de agua recogida?

b) En que instante se obtuvo la cantidad máxima de agua?

c) Cual fue esa cantidad máxima?

Solución

Teniendo en cuenta la regla de derivación de un cociente:

Si ,  su derivada es      f’(t)=

 

Y si queremos que sea cero, tiene que ser cero el numerador, de donde t =6

 

Señalamos el punto 6 en la recta y estudiamos el crecimiento de la función, f,  entre 0 y 12 (viendo el signo del numerador solo, pues el denominador siempre es positivo)

 

0                          6                          12

f ’      +                           -                          

Crece hasta el 6 y decrece desde el 6

Por lo tanto en 6 tiene un máximo relativo, que en este caso es absoluto (pues en el infinito da 0) y se tiene:

a) la cantidad aumenta en el periodo de 0 a 6

b) en t =6

c) f(6)=10/1=10

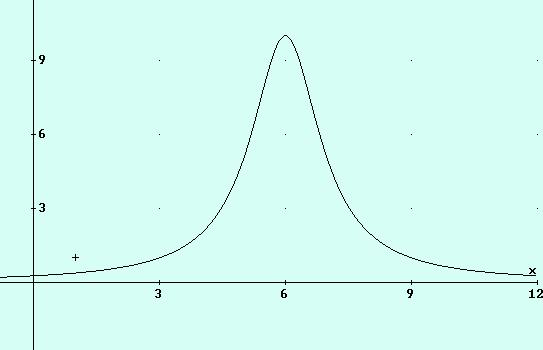
NOTA IMPORTANTE: EN ESTE TIPO DE PROBLEMAS CASI NUNCA ES ACONSEJABLE DESARROLLAR  EL DENOMINADOR.

 

8. La suma de dos números no negativos es 36. Halla dichos números para que:
a) La suma de sus cuadrados sea lo mas pequeña posible
b) La suma de sus raíces cuadradas sea lo mas grande posible

Solución

Sea x e y dichos números, se tiene x + y = 36, de donde y = 36-x

a) Definimos f(x, y)= x²+ y², como y= 36 –x, podemos sustituir en f con lo q dependerá solo de una variable, f(x) = x²+(36-x)²,  y podremos aplicar la condición necesaria de extremo para funciones derivables.

Derivando:

f’(x) = 2x-2(36-x), de donde f’(x) = 4x-72

Para que f tenga un mínimo la derivada debe darnos 0, por lo que 4x-72=0 y despejando x= 18

f es continua en el intervalo [0, 36], y f(0)=f(36)=(36)²>f(18)=2.(18)² por lo tanto en x=18 tiene el mínimo absoluto.

La gráfica es:

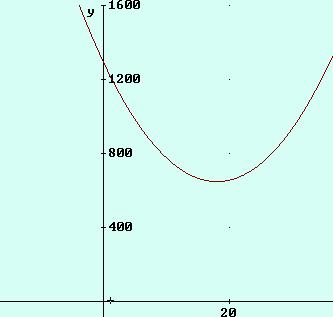
Observación: Otra forma de justificar que el mínimo es absoluto, es diciendo que la función f es cuadrática. Por lo tanto en la abscisa del vértice se alcanza su mínimo (a>0) que es el punto de tangente horizontal.

 

b) Teniendo en cuenta que y= 36 –x, tenemos h(x)= , derivando:

, h’(x)=0, elevando al cuadrado ambos miembros y operando se llega a que x=18.

La función h está definida en el intervalo [0, 36], luego el máximo lo tendrá en 18 pues:

f(18)= , y f(0=f(36)=6 (Observa que el menor valor posible lo alcanza en 0 y 36)

 

la gráfica es: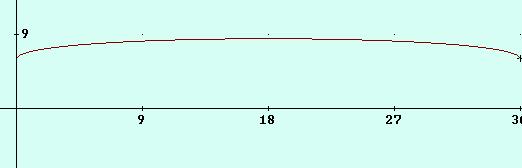

 

(Observar que no es necesario calcular la derivada segunda para el cálculo de los extremos absolutos, se aplica el teorema de Bolzano-Weierstrass que dice: “toda función continua definida en un intervalo cerrado alcanza su máximo y su mínimo”)

 

 

Si necesitas teoría visita la siguiente página:

Derivadas y sus aplicaciones  (apartados 5, 6 y 7)