1. A un vendedor de ordenadores le cuesta 140000 ptas. cada modelo de la marca PCHE-COMPR. Ha comprobado que al precio de 240000 ptas. unidad, vende 30 ordenadores mensualmente y que por cada 2000 ptas. de descuento en el precio puede vender 3 unidades más al mes. Hállese a que precio debe venderlos para obtener el máximo beneficio posible.
2. Se define una función del
modo siguiente: F(x)=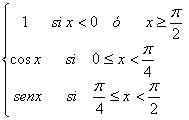
a) Hallar el dominio de definición.
b) Determinar la función derivada y dar su dominio.
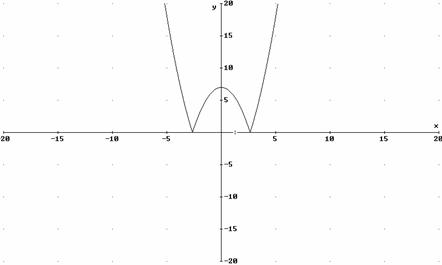
3. Dada la función y=
, se pide:
a) Representarla gráficamente.
b) Ecuación de la recta tangente en el punto de abscisa x=1.
c) Hallar sus máximos y mínimos relativos.
4. Estudiar la continuidad de las siguientes funciones:
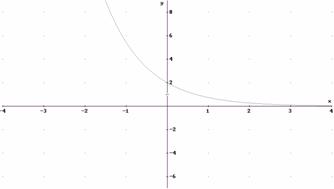
a) f(x)= 2e-x; b)
g(x)= 
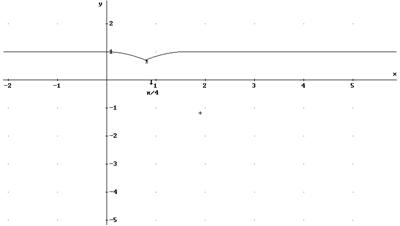
5. Estudiar los máximos y
mínimos de la función: y= 
¿los posee absolutos?
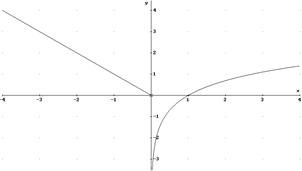
6. Representación gráfica de 
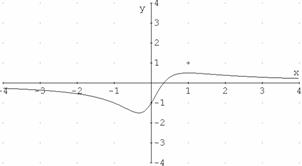
7. La gráfica de una función entre x=-2 y x=4 es la siguiente:
 |
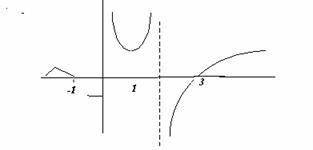a) ¿En qué puntos no es continua la función?
b) ¿En cuáles no es derivable?
c) ¿Cuál es su dominio?
d) ¿Qué se puede decir de las rectas x=0 y x=2?
9. Hallar a y b para que la función f(x)=x3+ax+b tenga un máximo en el punto (1,1)
10. Estudia y representa 
 |
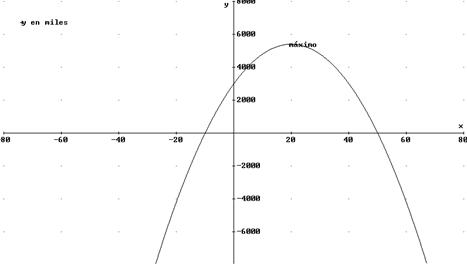
11. Cierta entidad financiera lanza al mercado un plan de inversión cuya rentabilidad, R(x), en miles de ptas. viene dada en función de la cantidad que se invierta x, en miles de ptas. por medio de la siguiente expresión:
R(x)= -0,001x2+0,5x+2,5
a) Deducir razonadamente la cantidad de dinero que le conviene invertir a un cliente en dicho plan .
b) ¿Qué cantidad obtendría?
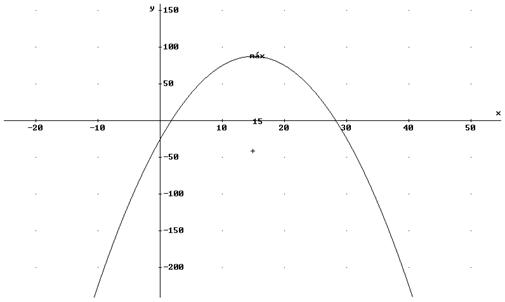
12. El coste de producción de x unidades diarias de un determinado producto es:
y el precio de venta de uno de ellos es (50-x/4) ptas.
Halla el número de unidades que debe venderse diariamente para que l beneficio sea máximo.
13. La segunda derivada de un polinomio de 2º grado que pasa por el punto (1,17) es 4. Halla el polinomio si se sabe que tiene un mínimo en x=1.
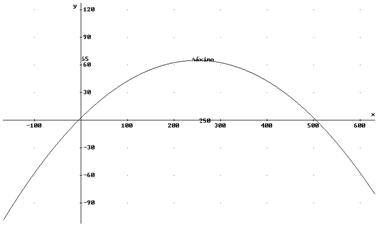
14. En 1980 se fundó una asociación ecologista. Se sabe que el número de sus miembros ha variado con los años de acuerdo con la función.
N(x) = 50(2x3 - 15x2 + 36x + 2)
a) Cuántos fueron los socios fundadores?
b) En qué períodos de tiempo aumenta el número de socios?
15. En una oficina de correos sólo se admiten paquetes con forma de paralelepípedo rectangular, tales que la anchura sea igual a la altura y, además la suma de sus tres dimensiones debe ser 72. Hallar las dimensiones del paralelepípedo para que el volumen sea máximo.
16. Dadas las funciones f(x) = 4x – 3 y g(x) = x2 determinar:
a) f o f.
b) Representar gráficamente la función g o f, especificando en qué punto alcanza los valores extremos.
17. Encontrar las funciones polinómicas
cuya
derivada segunda sea (x-1). ¿Cuál de ellas tiene un mínimo en el punto
(4,-1/3)?.
18. Se quiere cercar un terreno rectangular, situado junto a una carretera. Si la valla que está junto a la carretera cuesta a 2400 ptas. por metro y la del resto a 1200 ptas. , hallar el área del mayor campo que se puede cercar con un presupuesto de 432000 ptas.
19. De todos los rectángulos isósceles de 30 cm de perímetro, ¿cuál es el de área máxima?
20. Hallar el radio y la altura del cilindro de volumen máximo que se puede inscribir en una superficie esférica de 24 cm. de radio.
21 Un jardinero tiene que hacer un jardín con forma de sector circular de 120 m de perímetro. ¿ Qué radio le debe dar para que su superficie sea máxima?
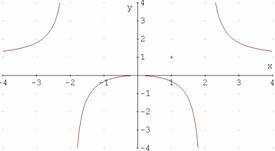
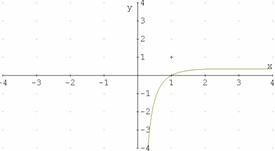
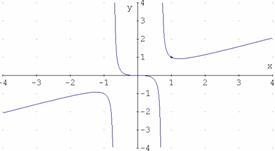
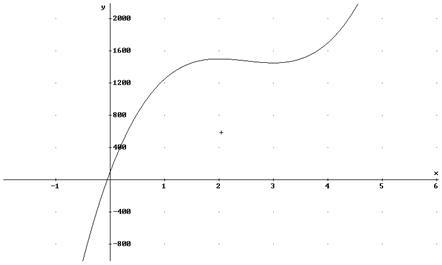
Gráficas de ejercicios propuestos.
y=
