M A T R I C ES

SI NO VISUALIZAS BIEN LA PÁGINA EXISTE EN FORMATO pdf. O TE LA PUEDES DESCARGAR EN zip

INTRODUCCIÓN

  En el tema anterior hemos usado la  “matriz  ampliada” de un sistema, para manejar, con más comodidad, los números que intervienen en un sistema lineal. En otros muchos problemas es útil disponer y manejar un conjunto de números dispuestos en filas  y columnas. Así es cómo se introdujo, en matemáticas, el concepto de matriz, como una disposición rectangular de números. Vienen a ser como una ampliación del concepto de número definiéndose para ellas operaciones como la suma y el producto.

 

1. Concepto de matriz. Elemento y orden de una matriz.

Definición. Se llama matriz del tipo mxn a un conjunto de m.n números dispuestos en m filas y n columnas:

columna

fila = A

Se escribirá A= (a_ij)

Se llama orden, tipo, o dimensión  de una matriz, al tamaño mxn.

Ejemplo1: A =es una matriz de orden 2x4, es decir, tiene dos filas y cuatro columnas.

Ejemplo 2. En un curso de 30 alumnos se han realizado cuatro evaluaciones, por lo tanto existen cuatro notas por cada alumno y los resultados se pueden disponen mediante una matriz:    

 

                    Evaluaciones

              ^Alumnos

Ejercicio 1. Un fabricante produce tres tipos de clavos: de aluminio (A), de cobre (Q) y de acero (H). Todos ellos se fabrican en longitudes de 1, 1’5, 2 y 2,5 cm. con los precios respectivos siguientes:

Clavos A:	0,20	0,30	0,40	0,50	pts
Clavos  Q:	0,30	0,45	0,60	0,75	pts
Clavos H:	0,40	0,60	0,80	1,00	pts

 

Recoger la información en una matriz 4x3 que recoja los precios.

El conjunto de todas las matrices de orden mxn se representa M_mxn.

A cada número a_ij  se le llama elemento o término de la matriz. El primer subíndice, y, indica la fila en que se encuentra el elemento, el segundo subíndice, j, la columna.

Dos matrices A y B , de M_mxn , son iguales si a_ij = b_ij para todo los i,j.

 

2. Tipos de matrices

Definiciones. La matriz se llama:

· Matriz fila, si tiene sólo una fila.

· Matriz columna, si tiene sólo una columna.

· Matriz nula,  O, si todos sus elementos son 0.

·Matriz traspuesta de A y se designa A’ o A^t, a la que se obtiene cambiando filas por columnas.

Ejercicio 2. Calcula la matriz traspuesta de A =

 

· Matriz cuadrada, si tiene el mismo nº de filas que de columnas.

Si tiene n filas se dirá, simplemente, de orden n (en vez de nxn).

Los elementos a_ii  (i=1,2...,n) forman la diagonal principal de la matriz

 

en esta matriz están indicados los elementos que forman la  diagonal secundaria.

·Matriz diagonal[ la que todos sus elementos, excepto los de la diagonal principal, valen cero. Es decir a_ij= 0, cuando y ¹ j.

En particular, si todos los elementos de la diagonal son 1, se la llama matriz identidad, I, o unidad.

Ejercicio 3. Escribe la matriz identidad de orden 5.

· Matriz triangular , superior si todos los elementos situados debajo de la diagonal principal son 0. Análogamente se define triangular inferior.

Ejemplo 3. La matriz 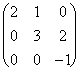 es triangular superior.

· Matriz simétrica, si coincide con su transpuesta, es decir a_ij = a_ji.

Ejemplo 4. La matiz identidad es una matriz simétrica.

Ejercicio 4. Sean A y B dos matrices cuadradas de orden 3, a_{ij =} 2i  - j , b_ij = . Se pide:

a) Escribe A y B

b) ¿Son simétricas?

 

3. Operaciones con matrices.

I) Suma de matrices.

Sean A= (a_ij) y B = (b_ij) dos matrices de orden mxn.  Se define la matriz suma de A y B como la matriz de orden mxn dada por:

 

 

La suma de matrices, así definida,  es una operación interna en el conjunto de las matrices de oren mxn, M_{m,n   ,}  verificándose además las siguientes:

 

Propiedades.  Asociativa,  conmutativa, elemento neutro (la matriz O), y elemento opuesto.

 

Por tanto el conjunto M_m,n  con + es un grupo aditivo.

 

II) Producto de una matriz  por un número

Se define el producto de la matriz A = (a_ij) por el número real k así:

 

 

Propiedades. 1) (k + m ) A = kA + mA

2) (km) A = k(mA)

3) k (A +B) = kA + kB

4) 1.A = A

 

Consecuencia: El conjunto de las matrices mxn con las operaciones suma y producto por escalares es un espacio vectorial.

 

III) Producto de matrices[

Se define el producto de la matriz A = (a_ij), de orden mxn, pr la matriz B = (b_ij), de orden nxp, como la matriz C= (c_ij) de orden mxp, obtenida así:

Observación: Para que dos matrices, A y B,  se puedan multiplicar tiene que ocurrir que el número de columnas de A sea igual al de filas de B

 Propiedades. 1) Asociativa, es decir  A(BC) = (AB)C

2) (A +B ) C = AB +BC y A(B +C) = AB +AC

Notas:

1) El producto de matrices, en general, no es conmutativo.

Ejemplo 4. = ,

   =        luego no es conmutativo.

2) El producto de matrices tiene divisores de cero, es decir, podemos encontrar dos matrices no nulas cuyo producto sea la matriz nula.

Ejemplo 5. =

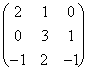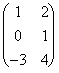Ejercicio 5. Sean A = , B = , C =.

a) Calcula A. B. ¿se puede verificar A.B = B.A? , razona la respuesta.

b) Calcula  A.(B.C) y (A.B)C.

4. Matrices cuadradas. Matrices regulares.

Si llamamos M_n al conjunto de las matrices cuadradas de orden n se verifica que con las operaciones + y · , definidas anteriormente,  es un anillo^[1].

La unidad para el producto es la matriz identidad, I.

La simétrica para el producto, que llamaremos inversa, en general no existe.

Ejemplo 6. no tiene inversa^[2].

Cuando una matriz A posea inversa diremos que es regular o inversible, y,  por definición, esto ocurrira si existe otra matriz, que representaremos por A^-1,  que verifique :

 (3)

 

 

Cálculo de la matriz inversa

Cuando una matriz sea regular se nos plantea el problema de cómo calcular su inversa. Hay varios métodos.

1º) Resolviendo el sistema que plantea (3).

 El nº de incógnitas que tiene este sistema es n². Se empleará para matrices de orden 2.

Ejemplo 6. Sea  A=  y llamemos a la inversa A^-1 = .

Tendríamos  que = , por definición de inversa.

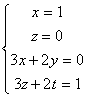de donde: = ÞÞ

A^-1=      (Comprobarlo^[3])

 

2º )  Mediante transformaciones elementales

   Si la matiz A se somete a ciertos cambios hasta obtener  I , sometiendo a I a los mismos cambios llegamos a la inversa.

Ejemplo 7. Vamos a calcular la inversa de A=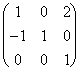

Cómo debemos hacer a I las mismas transformaciones que a A, la  siguiente colocación nos ahorrará tiempo y trabajo:

^{F1 - 2F3        F2 + F1}

, por lo tanto A^-1 =

 

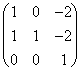
5. Forma matricial de un sistema de ecuaciones

Consideremos un sistema lineal de m ecuaciones con n incógnitas. Teniendo en cuenta cómo se multiplican las matrices se puede escribir:

,

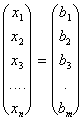 que se escribirá AX =B (2)

            A = matriz de los coeficientes del sistema.

X = matriz columna de las incógnitas.

B = matriz columna de los términos independientes.

Nota: Si la matriz A es cuadrada, es decir m=n, y  regular, el sistema resulta compatible determinado y  X =A^-1B. Lo estudiaremos con detalle en el tema siguiente.

Ejemplo: Sea el sistema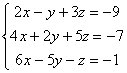, en forma matricial se escribiría:

 

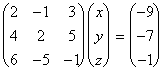
Ejercicios resueltos

1. De una matriz se sabe que es idempotente (es decir, que se cumple A² =A). Se define B= A-I,  donde I es la matriz unidad nxn. Calcular A^pB^qA^r, donde p,q y r son números enteros positivos.

Solución

Como A es idempotente, entonces Aⁿ= A para todo n.

B² = (2A-I)(2A-I)= 4A² - 4A.I + I² = 4A -4A + I = I ® B³ = 2A - I....

por lo tanto:  si q es par B^q = I, si q es impar B^q = 2A - I.

Tendremos , A^pB^qA^r = AIA= A , si q par

A^pB^qA^r= A(2A-I)A= (2A²-A)A =(2A-A)A= A.A=A si  q es impar

 

 

 

2. Un almacén clasifica naranjas según calidades en Inferior, Media, Buena y Superior. Los precios por kg. de cada una de estas calidades son , respectivamente, 20, 30, 50 y 80 pts. En tres días consecutivos un agricultor llevó al almacen las cantidades, en kg., que a continuación se detallan:

	Inferior	Media	Buena	Superior
primer día	1000	1000	500	500
segundo día	2000	1000	1000	1500
tercer día	1000	1500	600	1300

 

Todos los datos que se piden a continuación deben obtenerse como resultado de operaciones con matrices.

a) ¿Cuánto cobró el primer día ?

b) ¿Cuánto recibió por el total recolectado de naranja de tipo medio y superior?

Solución:

a)

b).

(Buscar otra forma de expresarlo)

3. a)Calcular una matriz X que verifique la igualdad:

AX = B,         con A =y  B =

b)¿ Verifica también la matriz X la igualdad  XA = B ?

Solución

Aunque se puede resolver planteando el sistema de 4 ecuaciones con 4 incógnitas que determina la ecuación matricial, es más corto usando que  A es inversible^[4] y por lo tanto  X = A^-1B, 

4. Dada la matriz  A = 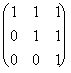, calcula A², A³ .....Aⁿ  .

Solución:

Se tiene:       A² ==;

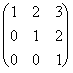A³ = A².A ==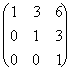;.....  Aⁿ   =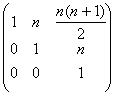  

 

5). Supongamos que son tres los sectores de economía de un país: 1.agrario, 2.industrial, 3.servicios. Datos del año 1994:

1. Del sector agrario se conocen los siguientes datos estadísticos ( en miles de millones): 9 en productos del propio sector, 3 del sector 2, 1 del sector 3; siendo la demanda total en el sector 12.

2.  El sector industrial empleó: 12 en materias del sector 1, 31 en los propios productos industriales, y 10 en servicios; la demanda final 47.

3.  El sector de servicios demanda del 1 0, del 2 6 y del propio 5; siendo el total de la demanda en el sector 31. 

Se piden:

1º.  Construir la tabla input-output]

2º. Calcular la matriz de los coefiecientes técnicos (matriz tecnológica)

Solución

1º)

		comprador			Demanda	output
		1	2	3	final	total
ven	1	9	12	0	12	33
de	2	3	31	6	47	87
dor	3	1	10	5	31	47

 

2º) La matriz de las transacciones intersectoriales  es:

X=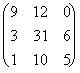, luego   A = 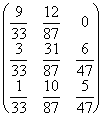= es la matriz tecnológica.

 

Ejercicios propuestos

 

1. Dadas las matrices A de orden 3x2, B de orden mxn y  C de orden 4x5, se sabe que se pueden multiplicar:  A.B.C . a) ¿De qué tipo es la matriz B?. b) ¿De qué tipo es la matriz A.B.C?.

2. La matriz:

postre: A    B    C   D

           = P

nos muestra el número de alumnos en una comida distribuidos según los cursos y la clase de postre que han pedido cada uno. A todos los que han pedido el postre A, la casa les obsequia con 6 vales a canjear a la salida y 3 boletos para un sorteo. A todos los que han pedido el postre B les obsequia con 8 vales y 5 boletos. A los que han pedido el postre C les dan 12 vales y 10 boletos, mientras que a los que han pedido el postre D les dan 5 vales y 2 boletos.

Utilizando las matrices responde a las siguientes preguntas:

a) ¿Cuántos vales recogen los alumnos de 2º?

b) ¿Cuántos boletos recogen los alumnos de Cou?

c) ¿Cuántos vales recogen entre todos?

d) Qué representa la suma de los elementos de las filas de P

3. Dada la matriz:

A= 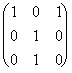, calcula Aⁿ.

4. Dada la matriz:

A= 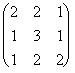   se pide: 

a) Obtener la traspuesta de A.

b) Calcular  (A-I)². (A-5I), siendo I la matriz unidad.

5. Dadas la matrices A = y B=, hallar las traspuesta de Ay B.

Comprobar que (A.B)^t = B^t. A^t.

6. Siendo A y B matrices cuadradas del mismo orden, decimos que A es una raíz cuadrada de B y escribimos   si    . Utilizando las matrices diagonales probar que  no es única.

7. Halla la inversa de A=. Resuelve la ecuación: , siendo X una matriz de orden 2.

 

 

Si quieres mas ejercicios del tema puedes encontrarlos en Selectividad  y en Ejercicios modelos examen    

 

Álgebra 2º Bach                                                       Matemáticas en el Bachillerato