ESTA PÁGINA RECOGE LAS SOLUCIONES DE LOS EJERCICIOS DE SELECTIVIDAD PROPUESTOS EN LA COMUNIDAD VALENCIANA EN EL AÑO 2004 (SI QUIERES LOS DE OTROS CURSOS VISITA SELECTIVIDAD)

 

SI TIENES PROBLEMAS PARA VISUALIZAR LAS FÓRMULAS PUEDES BAJARTE EL ARCHIVO DOC SOLUCIÓN 2004

 

JUNIO 2004

Ejercicio A

Problema 1 . Dadas las matrices:

       

Calcular la matriz X que verifica la ecuación AXB =2C

Solución

Se verifica A-1AXBB-1= X = A-12CB-1

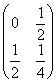Se tiene A-1=, B-1=, por tanto X ==

 

 

Problema 2. Un banco dispone de 18 millones de euros para ofrecer préstamos  de riesgo alto y medio , con rendimientos del 14% y 7% respectivamente. Sabiendo que se debe dedicar al menos 4 millones de euros a préstamos de riesgo medio y que el dinero invertido en alto y medio riesgo debe estar a lo sumo a razón de 4 a 5, determinar cuánto debe dedicarse a cada uno de los tipos de préstamos para maximizar el beneficio y calcular éste

Solución

Sea x lo que dedica a préstamos de riesgo alto

       y lo que dedica a préstamos de riesgo medio.

Función objetivo: f(x, y)= 0,14x+0,07y

Restricciones:

         R

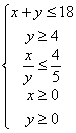
Luego queremos hacer máxima la función objetivo en la región factible que nos dan las restricciones

Dibujamos la región factible:

Dibujamos  las rectas auxiliares en el primer cuadrante, ya que tienen que ser valores positivos:

1) x +y =18  (la solución la parte de abajo)

2) y =4 paralela al eje X (solución la parte de arriba)

 

3) , es decir 5x= 4y,         ó        5x-4y=0 , ( y =5x/4) (solución la parte de arriba)

 

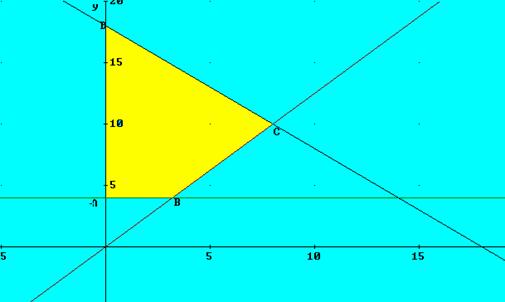
La región factible es lo relleno de amarillo  en el dibujo(ver figura abajo)

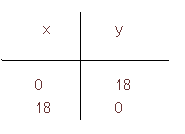
Los vértices son : A (0, 4) [ punto de intersección del eje Y, recta x =0, con y =4]

B(16/5 , 4)  [punto de intersección de las rectas  y = 4 ,  5x-4y=0,  que da x =16/5, y =4]

C(8, 10)  [punto de intersección de las rectas  x +y =18  y  5x-4y=0, comprobarlo)

D (0, 18) [punto de intersección de la recta 5x-4y=0 con el eje Y]

Si sustituimos estos valores en la función objetivos concluimos que el mayor valor se obtiene en (8, 10) (comprobarlo) luego es la solución óptima del problema y el valor máximo f( 8, 10) =1, 82 millones de euros

 

 

Hacerlo por el método gráfico.

 

Problema 3. Una multinacional ha estimado que anualmente sus ingresos en euros vienen dados por la función f(x)=28x2 + 36000x, mientras que sus gastos (también en euros) pueden calcularse mediante la función G(x)= 44x2 + 12000x + 700000, donde x representa la cantidad de unidades vendidas. Determinar:

a) La función que define el beneficio en euros.

b) La cantidad de unidades que deben ser vendidas para que el beneficio sea máximo. Justificar que es máximo.

c) El beneficio máximo.

Solución

a) El beneficio es la diferencia entre los ingresos y los gastos es decir:

B(x)=f(x)-G(x)= 28x2 + 36000x –(44x2 + 12000x + 700000) = -16x2+24000x-700000

b) Cómo la función beneficio es derivable, la condición necesaria para que tenga un máximo es que su derivada sea 0.

B´(x)=0-32x+24000=0, de donde x =

Para justificar que es el máximo hay varios métodos, por ejemplo: se calcula B´´(x)=-32< 0, que es la condición suficiente de máximo local.

Como cuando x tiende a + y - infinito la función tiende a –infinito estaría probado que es el mayor valor de la función.

Nota. Otra forma de justificar que el máximo es 750, sería estudiando el crecimiento en un entorno de 750 y viendo que crece hasta ese valor y decrece a partir de él. Y, por último, otra forma muy simple de justificarlo este hecho sería: observando que la función beneficio es un función cuadrática y su gráfica es una parábola, como a < 0 el vértice es el punto mas alto (punto de tangente horizontal, la derivada 0) y en este punto la abscisa es 750.

Resolución gráfica

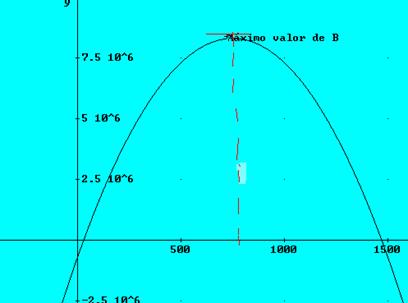
c) El beneficio máximo es B(750)=-16(750)2+24000.750-700000=8300000 euros

 

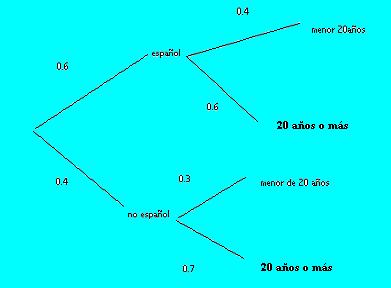
Problema 4. El 60% de las personas que visitaron un museo durante el mes de mayo eran españoles. De éstos, el 40% eran menores de 20 años. En cambio, de los que no eran españoles, tenían menos de 20 años el 30%. Calcular:

a) La probabilidad de que un visitante elegido al azar tengo menos de 20 años.

b) Si se escoge un visitante al azar, la probabilidad de que no era español y tenga 20 años o más

Solución

a) Por el teorema de la probabilidad total p(menor de 20 años) =p(español).p(menor de 20 años/español)+p(no español).p(menos r de 20 años/no español) =0,60.0,40+0,40.0,30=0,36

b) p(no español y 20 años o más) = p(no español).p(20 años o más/no español)= 0,40.070= 0,28

(Ver diagrama de árbol )

Ejercicio B

Problema 1. Juan decide invertir una cantidad de 12000 € en bolsa, comprando acciones de tres empresas, A, B y C. Invierte en A el doble que en B y en C juntas. Transcurrido un año. Las acciones de la empresa a se han revalorizado un 4%, las de B un 5% y las de C han perdido un 2% de su valor original. Como resultado de todo ello, Juan ha obtenido un beneficio de 432,5 € . Determinar cuánto invirtió Juan en cada una de las empresas.

Solución

Sea x la cantidad invertida en la empresa A

Sea y la cantidad invertida en la empresa B

Sea z la cantidad invertida en la empresa C

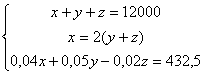
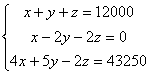
Se verifica     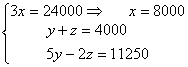     (reducción)

 

 

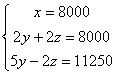
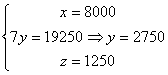
(hacerle usando el método de Gauss)

Problema 2. Un tren de mercancías puede arrastrar, como máximo, 27 vagones. En cierto viaje transporta coches y motocicletas. Para coches debe dedicar un mínimo de 12 vagones y para motocicletas no menos de la mitad que dedica a los coches. Si los ingresos de la compañía ferroviaria son de 540 € por vagón de coches y 360 € por vagón de motocicletas, calcular cómo se deben distribuir los vagones para que el beneficio de un transporte de coches y motocicletas sea máximo y cuánto vale dicho beneficio

Solución

Llamamos

x  nº de vagones dedicados a coches

y  nº de vagones dedicados a motocicletas

La función objetivo es f(x, y)= 540x +360y

Las restricciones vienen dadas por:

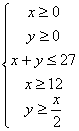
Para calcular la región factible dibujamos las rectas auxiliares:

1) x +y =27 (usamos los puntos de corte con los ejes (0, 27) y (27, 0) ) la solución de la inecuación es el semiplano inferior a la recta

2) x = 12    (paralela al eje de las Y que pasa por el (12, 0) ) la solución es a la derecha del 12

3) y = x/2 (la dibujamos usando los puntos (0, 0) y (12, 6)) la solución de la inecuación es el semiplano superior a la recta

Los vértices que se obtienen en este caso son: A(12, 6), B(18, 9) y C(12, 15), como se puede comprobar fácilmente

La región factible que resulta está coloreada en la figura:

 

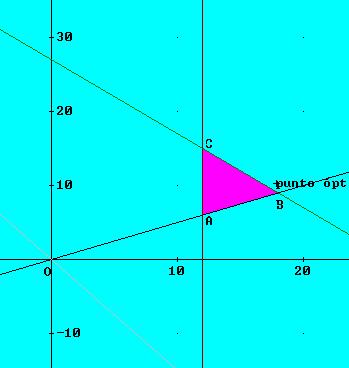
También se ha dibujado la recta f(x, y)=0 (en rojo) y se observa que el punto más alejado (dentro de la región factible) es el B y sería por tanto la solución gráfica del problema.

Lo comprobamos por el método analítico, es decir calculando los valores de la función objetivo en los vértices.

f(A)= 540.12+360.6=8640

f(B)=540.18+360.9=12960        este es el beneficio máximo pedido

f(C)=540.12+360.15=11880

Luego 18 vagones para coches y 9 para motocicletas.

 

Problema 3. La parte superior de una pared de 2 metros de base tiene una forma parabólica determinada por la expresión  -0,5 x2 + x + 1, donde x mide la longitud en metros desde la parte izquierda de la pared. Calcular la superficie de dicha pared utilizando una integral.

Solución

Aunque para resolver este problema no haría falta, porque no nos los pide expresamente,  dibujamos la parábola y=-0,5 x2 + x + 1

Puntos de corte:

Con el eje OY        x = 0,           y =1, (0, 1)

Con el eje OX        y = 0 = 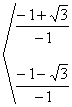[x = 2.73205, x = -0.732050], puntos (2,73, 0) y (-0,73, 0)

 

Vértice        xV =, yV =-0,5.12+1+1=1,5. V(1, 1,5)

Gráfica

 

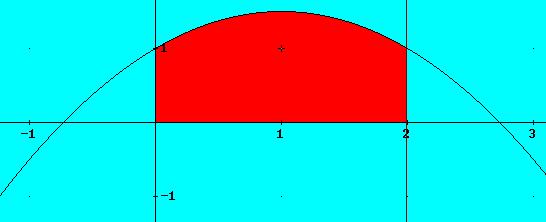
El área que nos piden es la coloreada de rojo, que se puede expresar como:

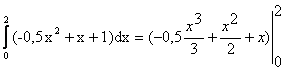=-(4/3) + 2+2= 8/3 m2

 

Problema 4. La máquinas A y B producen 50 y 250 piezas por hora, con un porcentaje de fallos de 1% y del 10%, respectivamente. Tenemos mezcladas las piezas fabricadas en una hora y elegimos una pieza al azar. Calcular:

a) La probabilidad de que sea una pieza no defectuosa fabricada en la máquina B.

b) La probabilidad de que esté fabricada en la máquina a, si sabemos que es defectuosa.

Solución

En primer lugar calculamos las probabilidades de que las piezas sean fabricadas en A o en B

En una hora se producen en total 50+250=300, entonces

p(A)= p(fabricada en la máquina A)=50/300=1/6, y p(B)=p(fabricada en la máquina B)=250/300=5/6

El diagrama de árbol expresa la situación y sus probabilidades, al elegir una pieza al azar:

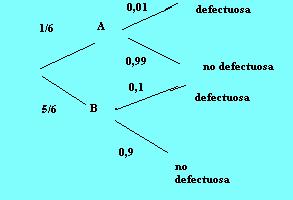
a) p(no defectuosa y fabricada en la máquina B)= p(B).p(no defectuosa/B)=(5/6).0,9=0,75

b) p(fabricada en la máquina A/defectuosa)=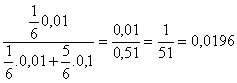

 

SEPTIEMBRE 2004

 

EJERCICIO A

Problema 1. Obtener la matriz X que verifica        AX – B = 3X

siendo:

A = 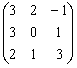 y B =

 

Solución

 

AX =3X+ B, 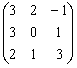 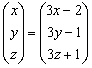, de donde obtenemos el siguiente sistema:

                           

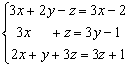
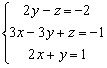     que resolvemos por reducción:

 

Sumando la 1ª ecuación con la 2ª se obtiene: 3x –y = -3. Sumada con la 3ª se obtiene 5x=-2, de donde x =-2/5

Sustituyendo obtenemos y = 1 + 4/5 = 9/5, z = 28/5

 

OBSERVACIÓN

Otro método sería encontrar la matriz inversa de (A-3I) y multiplicarla por B, ya que se verifica:

 

(A-3I)X = B, de donde X = (A-3I)-1B

Problema 2. Un fabricante produce en dos talleres tres modelos distintos de archivadores, el A, el B y el C. Se ha comprometido a entregar 12 archivadores del modelo A, 8 del B y 24 del C. Al fabricante le cuesta 720 € al día el funcionamiento del primer taller y 960 € el del segundo. El primer taller produce diariamente 4 archivadores del modelo A, 2 del B y 4 del C, mientras que el segundo produce 2, 2 y 12 archivadores, respectivamente ¿Cuántos días debe trabajar cada taller para, cumpliendo el contrato, conseguir reducir al máximo los costes de funcionamiento?. ¿Cuál es el valor de dicho coste? ¿Quedaría algún excedente de algún producto en los talleres? En caso afirmativo, determinar cuánto.

Solución

Llamamos x al nº de días que trabaja el primer taller, e y al nº que trabaja el segundo taller

 

nº días

A

B

C

coste

Taller 1

Taller 2

x

y

4x

2y

2x

2y

4x

12y

720x

960y

 

 

12

8

24

 

La función objetivo es C(x)= 720x+ 960y

Las restricciones

 

 

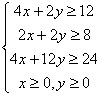
Dibujamos la región factible (representando las rectas auxiliares) y hallamos los vértices:

Los vértices son (0, 6), (2, 2), (3, 1) y (6, 0) (comprobarlo resolviendo los sistemas formados por las rectas auxiliares)

Usando el método gráfico se comprueba que el primer vértice q se encuentra es el (3,1) y por tanto la solución del problema, nosotros lo vamos a comprobar usando el método analítico, es decir calculando el valor de la función objetivo en cada uno de los vértices para ver en cuál se obtiene el mínimo coste.

C(0, 6)=5760, C(2, 2)=3360, C(3, 1)=3120 y C(6, 0)=4320 (comprobarlo)

Por tanto se tiene que trabajar 3 días en el primer taller y 1 día en el segundo taller

El valor de dicho coste es 3120 euros y queda un excedente de 2 archivadores de tipo A.

 

Problema 3. Un restaurante abre a las 8 de la noche y cierra cuando todos los clientes se han ido. La función C(t)= 60t – 10t2 representa el número de clientes que hay en el restaurante en función del número de horas t que lleva abierto el establecimiento. Se pide:

a) Determinar el número máximo de clientes que van una determinada noche al restaurante. Justificar que es un máximo.

b) Si deseamos ir al restaurante cuando haya al menos 50 personas y no más de 80, ¿entre qué horas tendríamos que ir?

SOLUCIÓN

En primer lugar vemos que el dominio de la función C es [0, 6], es decir el restaurante abre de 8 a 2 de la mañana.

a) Para que sea un máximo la derivada debe ser cero

C’(t)=60-20t

C’(t)=0 implica que 60-20t=0, de donde t =3 horas lleva abierto.

El número de clientes para t=3, es C(3)=60.3-10.32=90 clientes

Es máximo absoluto pues la función crece hasta llegar a 3 (C’>0) y decrece a partir del 3 (C’<0).

b) Queremos que se verifique:

50 C(t) 80

 

Resolviendo la inecuación  60t-10t250 (o lo que es igual: 10t2 -60t+500)  nos queda el intervalo [1,5]

Resolviendo  la inecuación 60t-10t280 nos queda (-][4, )

Haciendo la intersección nos queda [1, 2] [4, 5]

Por lo tanto tendría que ir entre las 9 y las 10, ó entre las 12 y la 1

Problema 4. Se ha realizado una encuesta a un grupo de estudiantes de informática. Entre sus conclusiones está que un 40% ha recibido algún curso de LINUX. Además, el 20% de aquellos que recibieron algún curso de LINUX tienen ordenador en casa. Si un 10% de estudiantes de informática tienen ordenador en casa y no han recibido ningún curso de LINUX, calcular:

a) La probabilidad de que un estudiante de informática tenga ordenador en casa y haya recibido un curso de LINUX.

b) La probabilidad de que un estudiante de informática tenga ordenador en casa.

c) si un estudiante de informática tiene ordenador en casa, la probabilidad de que haya recibido un curso de LINUX.

Solución

Se tiene p(O, NL)=0,1

Como p(O, NL) =p(NL).p(O/NL) entonces 0,1=0,6.p(O/NL), de donde p(O/NL)= 0,6/0,1=1/6

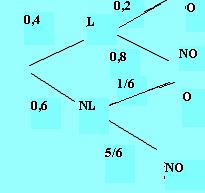
Por lo tanto:

a) p(O, L)=0,4.0,2=0,08

b) p(O)=0,4. 0,20 + 0,1=0,18

c) p(L/O)=

 

EJERCICIO B

Problema 1. Dos hijos deciden hacer un regalo de 100 € a su madre. Como no tienen suficiente dinero, cuentan con la ayuda de su padre, decidiendo pagar el regalo de la siguiente forma: el padre paga el triple de lo que pagan los dos hijos juntos y, por cada 2 € que paga el menor,  el mayor paga 3 €. ¿Cuánto dinero ha de poner cada uno???

Solución

Llamamos:

x  lo que paga el padre

y lo que paga el hijo mayor

z lo que paga el hijo menor

Se verifica:

x +y +z =100

x =3(y +z)

3z= 2y

Para resolverle no es necesario aplicar el método de Gauss, pero os lo aconsejo para practicar.

Comprobar que la solución es: x =75, y =15, z =10

Es decir el padre 75 euros y los hijos 15 y 10 euros respectivamente.

Problema 2. Calcular los puntos de la región definida por

 

 

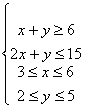
donde la función z = 3x +2y alcanza los valores máximo y mínimo. Calcula dichos valores

Solución

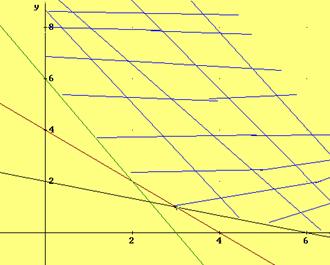
Dibujamos la región:

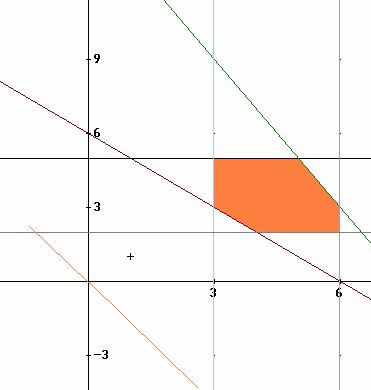
Como se aprecia en el dibujo los vértices son: (3, 3), (3, 5), (5, 5), (6, 3), (6, 2) y (4, 2) (comprobarlo)

Método gráfico: Si desplazamos la recta 3x+2y= 0 el primer punto que nos encontramos es el (3, 3) (mínimo) y el último el (5, 5) (máximo)

También podemos comprobar el resultado calculando los valores de z=3x+2y en todos los vértices (método analítico), (calcularlos)

En (3, 3) da 15 , valor mínimo, y en (5, 5) da 25, valor máximo.

 

Problema 3. Se quiere imprimir un cartel anunciador rectangular que debe contener 18 cm2 de texto impreso (también rectangular). Los márgenes superior e inferior deben ser de 2cm cada uno, mientras que los laterales deben ser de 1cm. Calcular las dimensiones del cartel para que el gasto del papel sea mínimo y justificar que dicho gasto es realmente mínimo.

Solución

Sean x e y las dimensiones del cartel, se tiene que hacer mínimo el área A=x.y con la condición de que

(x-2).(y-4)=18cm2

Despejamos la incógnita y, nos da

Sustituyendo en A, nos queda:

A==, donde x>2

Derivando e igualando a 0, se tiene:

A’ =, A’=0 implica que 4x2-16x-20=0, simplificando: x2-4x-5=0, cuyas raíces son 5 y -1, esta última no nos vale ya que x representa una dimensión (magnitud positiva)

Veamos si en x=5 se obtiene el valor mínimo de A, para eso estudiamos el comportamiento de A en un entorno de 5.

         -                           +       

2       decrece       5       crece

que nos da un mínimo relativo (comprobar que es absoluto)

Problema 4. En una población hay el doble de mujeres que de hombres. El 25% de las mujeres son rubias y el 10 % de los hombres también son rubios. Calcular:

a) Si se elige una persona y resulta rubia, ¿cuál será la probabilidad de que sea mujer?

b) ¿Cuál es la probabilidad de que una persona elegida al azar sea hombre y no sea rubio?

Solución

Puesto que hay el doble de mujeres que de hombres, p(H)=1/3 y p(M)=2/3

Vamos a calcular la probabilidad de ser una persona rubia.

P(R/M)=0,25, p(R/H)=0,10

P(R)= p(H)p(R/H)+ p(M)P(R/M)=

a) p(M/R)=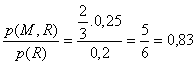

b) p(H, nR)=p(H).p(nR/H)=

 

Matemáticas aplicadas a las Ciencias Sociales II

 

 

Matemáticas para todos