4ª Parte: Geometría
Propiedades de las figuras planas y cuerpos geométricos
Poliedros regulares
La esfera. El globo terráqueo
1. Dibuja un triángulo equilátero e indica en él sus puntos notables: baricentro, incentro, circuncentro y ortocentro. ¿Qué observas?
2. En un triángulo equilátero, la circunferencia inscrita tiene un radio de 4cm. ¿Cuánto mide el radio de la circunferencia circunscrita?
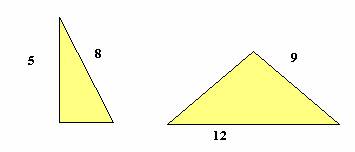
3. Calcula la longitud del lado desconocido de cada triángulo rectángulo:
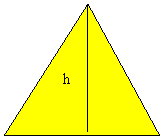
4. Calcula la altura de un triángulo equilátero de 10cm de lado.
Solución
Por ser equilátero la altura “cae” en el punto medio de la base.
Por
el teorema de Pitágoras h2 = 102 -52 =75 y 
5
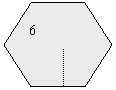
5. Calcula la longitud de la apotema de un hexágono regular de 6cm de lado
6 Calcula el radio de una circunferencia inscrita y el de la circunferencia circunscrita a un hexágono regular de 10cm de lado.
7. Los lados de un triángulo A’B’C’ miden el doble que los del ABC. Si la superficie del primero es 18dm2. ¿Cuál será la superficie del segundo?
8. La razón de las áreas de dos polígonos semejantes es 25/49. ¿cuál es la razón de sus lados?
9. Dos ciudades que en la realidad están a 900km, aparecen en el mapa separadas 6cm. ¿A qué escala se ha dibujado el mapa?
10. Calcula la distancia a que se encuentran 2 ciudades si en el plano están a 13 cm.
Datos: escala 1: 1800000.
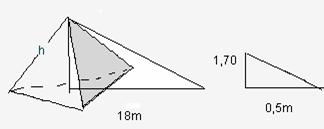
11. Calcula la altura de la pirámide sabiendo que la sombra que proyecta es de 18 m y que la sombra que proyecta Tales es de 0,5m. Nota. Tales mide 1,70 m
12. Halla la longitud del arco de curva y el área de un sector circular de 10cm y de ángulo 60º´
Solución
La
longitud del arco es 
=
10,472cm
El
área del sector circular 
=
=52,36cm2
13. Una nave tiene 12m de largo, 10m de ancho y 4m de alto. Se trata de llenarla de cajas cúbicas de 1m de lado. ¿Cuántas cajas se necesitan?
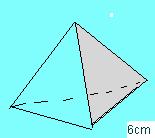
14. Calcula la superficie de un tetraedro regular de 6cm de arista.
Solución
El tetraedo regular está formado por 4 triángulos equiláteros de 6cm de lado
 |
|||
 |
|||
6 h = 
=
3 A
=
El área total AT = 4. 15,58=62,35cm2
15. Calcula el valor de las diagonales de los cubos cuyas aristas miden:
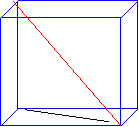
a) 1cm; b) 4cm
16. Un cono recto tiene 5cm de radio de la base y 14cm de altura. Calcula:
a) El área de la base; b)
El área lateral; c) El área total; d) El volumen del cono.
Solución
a) A B
= 
= 78,54; b) AL =
=233,57
g
g =
c) AT = 78,54 +233,57 = 312,11cm2 5
El
volumen del cono V = 
17. Calcular el área de la superficie de una esfera de 5cm de radio.
18. Si la superficie de una pelota mide 1325cm2 ¿cuánto mide su radio?
19. El radio de una esfera es 10cm. ¿Cuál es la altura de un casquete esférico cuya área es la cuarta parte de la superficie esférica?
20. Calcula los ángulos de los husos iguales determinados por:
a) 12 meridianos; b) 24 meridianos; c) 30 meridianos.
Solución : a) Los 12 husos
tienen 360º: por tanto un huso medirá 
21. Halla el área de la superficie de la tierra, si su radio es 6370km.
22. Halla la razón del área de la superficie terrestre a la de la Luna, admitiendo para diámetro de ésta 404km.
23. a) Hallar el área del huso esférico de la figura de ángulo 60º y radio 202km (de la Luna).
b) Halla el volumen de la cuña esférica limitado por el huso anterior y dos semicírculos máximos
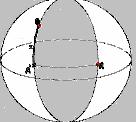60º
S
= 
=8546km2
V =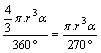
=5754299,77km3
24. Halla el volumen de una
esfera cuya área es 256
cm2.
25. Una esfera de plomo de 6,203cm de diámetro por fusión y moldeo se ha convertido en cubo. ¿cuál será el volumen de éste? ¿Y cuál su arista?
Transformaciones geométricas
Movimientos en el plano: Traslaciones, giros y simetrías.
Homotecias.
1. Dados los puntos A(-1, 4)
y B(2, 3) calcula las coordenadas de los vectores 
y 
.¿Cómo
son entre sí estos vectores?. Dibújalos.
2.En una traslación de vector v = (2, 3), se sabe que el transformado del punto C es C’(-3, 6). Halla las coordenadas del punto C.
Solución. La ecuación de la traslación es
(x’, y’) = (x, y)+ (v 1, v2)., sustituyendo (-3, 6) = (x, y) + (2, 3), de donde:
-3 = x +2 Þ x =-5
6 = y +3 Þ y = 3 C(-5, 3)
Compruébalo gráficamente.
3. En una traslación de vector v el punto A(1, 0) se transforma en el A’(3, 4). Determina las coordenadas de v.
4. Dibuja el triángulo de coordenadas A(0, 0), B(1, 1) y C(1,0). Hazle una traslación de vector v=(2, 3), ¿qué coordenadas tiene el triángulo trasladado?. Comprueba tu observación calculando las coordenadas mediante la ecuación de traslación (x’, y’) = (x, y)+ (v 1, v2).
5. Comprueba que la aplicación de dos traslaciones sucesivas de vectores u y v es otra traslación de vector u + v (se llama también producto de traslaciones). Aplica al triángulo de vértices A(0, 0), B(1, -1) y C(2,4) la traslación de vectores (3, 2) y (4, -2).
6. Dibuja un hexágono de lado 2cm y centro el origen O. Aplícale un giro de ángulo 60º y centro O ¿qué observas? ¿Y si el ángulo es de 120º?
7. Una noria de 15 m de radio tiene 18 cestillas.
a) ¿Qué ángulo tiene que girar para que la cestilla que está a ras de suelo se coloque a media altura?¿y a máxima altura?
b) ¿Qué ángulo tiene que girar para que una cestilla se coloque en el mismo lugar que la que va delante?
Solución
a) Para que se ponga a media altura tiene que girar 90º ó 270º.
b) 360º:18=20º, luego hay que girar 20º.
8. Dibuja en un sistema de ejes coordenados un segmento de extremos A(3, -2) y B(0, 4). construye gráficamente el segmento homólogo mediante el giro de centro el origen y ángulo 45º.
9. Dibuja un vector y halla sus simétricos respecto los ejes coordenados.
10. Dado el triángulo de vértices A(0, 0), B(1, -1) y C(2,4) halla los triángulos simétricos respecto del eje OX y del eje OY
11. Construye un hexágono regular y dibújalo a escala 1/2.
12. Dibuja un cuadrilátero y toma un punto O de su plano. Si se toma O como centro de una homotecia de razón 2, halla el transformado del cuadrilátero en dicha homotecia.
Cuaderno de actividades de 3º ESO Cuaderno de actividades de 4º ESO
Matemáticas en la Secundaria Matemáticas para todos
Si tienes alguna duda o sugerencia puedes dejar tu mensaje en el Foro de Matemáticas en el Siglo XXI