ANÁLISIS DESCRIPTIVO DE FUNCIONES Y GRÁFICAS
(Con repaso de cursos anteriores)
INTRODUCCIÓN
La noción actual de función comienza a gestarse en el siglo XIV, cuando empiezan a preocuparse de medir y representar las variaciones de ciertas magnitudes, como la velocidad de un cuerpo en movimiento. El nombre de función proviene de Leibnitz. A partir de los siglos XVIII y XIX el concepto de función se hace el eje central de las matemáticas, su estudio a través del cálculo y sobre todo de las ecuaciones diferenciales se hace totalmente indispensable para llevar adelante todo el desarrollo científico y tecnológico, primero al servicio de la Física y luego de otros campos.
I) FUNCIONES Y GRÁFICAS
1. Concepto “intuitivo” de función. Las funciones como descripción de fenómenos
¿Qué son las funciones?
- la posición de un móvil es función del tiempo
- la presión atmosférica es función de la altura
- el peso medio de los chicos depende de la edad....
Expresiones semejantes ilustran bien lo que es una función en matemáticas. Las de arriba significan que:
- a cada tiempo le corresponde un espacio recorrido (a una velocidad determinada)
- a cada altura le corresponde una presión atmosférica
- a cada edad le corresponde un peso medio.
A esta asignación se le llama función.
El conjunto de elementos a los que se le asigna algo se llama el conjunto de definición o dominio de la función o campo de existencia. El conjunto de esos algos que se les va asignando se llama recorrido o conjunto imagen.
Ejemplo 1. Consideremos la función que a todo número se le asigna su inverso, el dominio de esta función es todos los reales menos el 0.
Ejemplo 2. La función que a un nº real se le asigna su raíz cuadrada está definida sólo para los positivos. Es decir su dominio son los reales positivos (incluido el 0)
2. Expresiones algebraicas de una función. Formas de determinar una función
Expresión simbólica de una función
Las que estudiaremos nosotros son las que a cada número de un cierto conjunto le asigna otro número: funciones numérica que llamaremos simplemente funciones.
Definición 1. Se llama función real de variable real a toda aplicación:
f : D ---------à R
x ------------à f(x) o y =f(x) siendo D Ì R el dominio.
La letra f simboliza la asignación u operación que hay que hacer a la x, que llamaremos variable independiente, al valor f(x) se le llama variable dependiente o imagen de x.
Ejemplo 3. La función f(x) =x2
Ejercicio 1. Hallar el dominio de las siguientes funciones;
a) ![]() ; b) g(x) = ln (x2+1); c) ; c) y =
; b) g(x) = ln (x2+1); c) ; c) y =![]() ; d)
; d) ![]()
Representación gráfica
El conjunto de todos los pares 8x, y) donde x recorre el dominio de f se llama la gráfica de f. La gráfica es una herramienta muy útil para visualizar propiedades y comportamientos de una función (Ver apartado 4)
Para representar una función se debe considerar:
- El dominio o campo de existencia
- Los cortes con los ejes
- El signo de la función. Regiones de existencia
- La simetría de la gráfica.
- Los intervalos de crecimiento.
–La relación con otras funciones conocidas.
Traslaciones y suma de gráficas. Representación conjunta de gráficas
En la figura 1 están representadas las gráficas de f(x)= x2 y la de g(x)=x2 -2
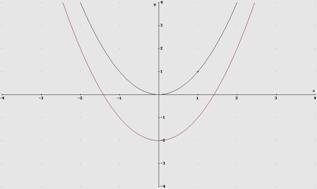
en la figura 2 están representadas las gráficas de f(x)= x2 y g(x) = (x +1)2
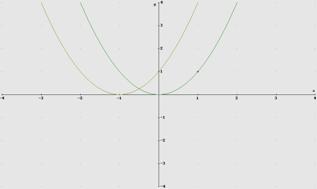
En la figura 3 están representadas las gráficas de las funciones f(x)=x2 , g(x)= x3 y h(x) = x2 +x3
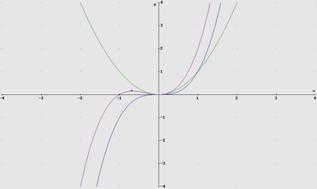
¨ Aplicación práctica: punto de equilibrio entre las curvas de oferta y demanda.
Ejercicio 2. Las curvas de oferta y de demanda de cierto tipo de ordenadores son, respectivamente:
y =2x- 1000
y = 0,5x +2000
en donde x es el precio en euros de los aparatos e y el número de aparatos ofertados o demandados. Hallar el punto de equilibrio.
Formas de determinar una función
Mediante
-Una fórmula. Ej.: E =v.t (poner de manifiesto sus ventajas)
-Su representación gráfica.
- Una serie de puntos.
- La descripción del fenómeno q representan.
Ejercicio 3. Un médico dispone de 1hora diaria para consulta. El tiempo que podría, por término medio, dedicar a cada enfermo, depende del número de ellos que se acudan:
![]() 1 enfermo
60 minutos
1 enfermo
60 minutos
![]() 2 enfermos 30
minutos
2 enfermos 30
minutos
![]() 3 enfermos 20
minutos
3 enfermos 20
minutos
..... ....... ......... ......
Así hasta un máximo de 30 enfermos. Si llamamos x al número de enfermos e y al de minutos dedicados a cada enfermo escribe la expresión funcional que existe entre ellas ¿ Cómo es la variable independiente, continua o discreta? Dibuja la gráfica ¿ Tiene sentido unir los puntos de la gráfica con una línea?
Ejercicio 4. En unos aparcamientos públicos figura la siguiente tarifa de precios:
Tarifa
![]() 1ª hora o fracción 1
€
1ª hora o fracción 1
€
![]() Cada hora más o fracción
0,8 €
Cada hora más o fracción
0,8 €
Máximo 12 € por 24 horas
Haz una gráfica representativa de la función : tiempo de aparcamiento ....... coste
Ejercicio 5. Un viajero quiere alcanzar un tren en marcha. Las funciones que relacionan el espacio y el tiempo son, en cada caso:
Viajero: SV =4t Tren: ST = 1+ 3t2
Representa las gráficas correspondientes. ¿Llega a producirse el alcance? ¿En qué momento?
3. Operaciones con funciones
a) Suma de funciones
Dadas dos funciones f y g se define la función suma g +g por:
(f +g)(x)=f(x)+g(x)
Se verifica que Dom (f +g)= Dom fÇDom g.
b) Producto de funciones
Dadas dos funciones f y g se define la función producto f.g así
(f.g)(x)= f(x).g(x)
Se verifica que Dom(f .g)= DomfÇDomg
c) Cociente de funciones
Dadas dos funciones f y g se define la función cociente f/g por:
(f/g)(x) = f(x)/g(x), siempre que g(x) sea distinto de 0.
Se verifica que Dom(f /g)= DomfÇDomg -{xÎR/g(x)¹0}
d) Composición de funciones
Dadas las funciones f y g se define la función compuesta de f y g
(fog)(x) = f(g(x))
Se verifica que Dom (fog)= {xÎDom f / f(x) ÎDom g }ÌDom f
Observación. El dominio de la composición a veces no coincide con el dominio de la función resultante de efectuar las operaciones indicadas en la composición.
Ejemplo 4. Consideramos
f(x) = ![]() y g(x)=x2, el dominio
de (gof) es [0,
y g(x)=x2, el dominio
de (gof) es [0, ![]() ) y efectuando las operaciones
indicadas la composición da h(x9 =x, cuyo dominio, aparentemente, sería todo R.
) y efectuando las operaciones
indicadas la composición da h(x9 =x, cuyo dominio, aparentemente, sería todo R.
La composición de funciones no posee la propiedad conmutativa.
Ejercicio 6. Dadas las funciones f(x)= x +3 y g(x)= x2 calcula gof y fog.
FUNCIÓN INVERSA
Si f : D------------à R es inyectiva, existe una función g: Imf----------à D tal que gof =I, I(x) =x para todo x del dominio de f (I se llama identidad). A g se le llama la inversa de f y se representa en general por f -1.
Las gráficas de f y f-1son simétricas respecto a la bisectriz del primer y tercer cuadrante.
Cálculo práctico de la inversa
Si y = f(x) la expresión de f-1 se obtiene despejando la x:
Ejercicio 7. Calcula la inversa de a) ![]() ; b)
; b) ![]() .
Comprueba el resultado.
.
Comprueba el resultado.
4. Interpretación de gráficas. Qué aspectos de la gráfica conviene estudiar
Cuando se nos presenta la gráfica de una función, nos basta una simple ojeada para conocer como es dicha función e intuir sus propiedades.
Para hacer una interpretación acertada de la gráfica no es preciso tener grandes conocimientos matemáticos, pues se puede intuir:
- Dominio de f.
- Simetría (funciones pares e impares)
- Crecimiento y decrecimiento.
- Máximos y mínimos absolutos y relativos (muy fáciles de determinar si tenemos la gráfica)
- Ramas infinitas: AV, AH, AO
- Periodicidad
Ejercicio 8. Interpretar la siguiente gráfica
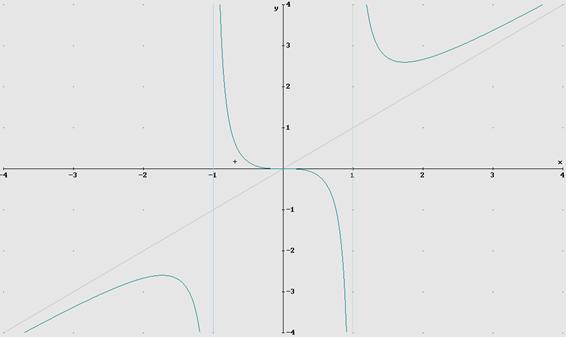
5. Tipos de funciones mas “frecuentes”. Sus gráficas.
-Funciones polinómicas de 1er grado (repasarlas)
-Funciones polinómicas de 2º grado (repasarlas)
- Funciones potenciales de exponente natural, y=xn
Su dominio es R.
Si n es par:
Estas funciones:
Son
![]()
Tienen el valor mínimo en (0, 0) y es 0.
Las gráficas son simétricas respecto al eje OY (funciones pares)
Pasan todas por los puntos (-1,1), (0, 0), (1, 1)
Si n es impar:
Estas funciones son crecientes para todo R (no tienen por tanto ni máximo ni mínimo)
Las gráficas son simétricas respecto al origen (funciones impares)
Todas pasan por los puntos (-1, -1), (0, 0), (1, 1)
- Funciones racionales
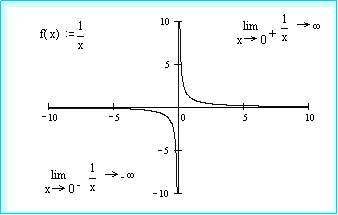
Caso particular f(x)=1/x (expresa la relación de la proporcionalidad inversa)
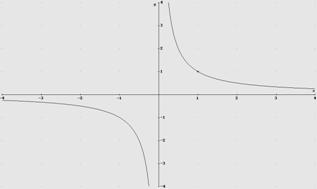
Estudiarlas.
-Funciones exponenciales, y = ax , a>0
Su
dominio es R y su recorrido es (0, ![]() )
)
Todas pasan por el punto (0, 1)
Si a>1
Son crecientes en todo R
Si x<0 entonces ax<1
Si
x tiende a -![]() entonces ax tiende a 0
(y =0 es una asíntota horizontal)
entonces ax tiende a 0
(y =0 es una asíntota horizontal)
Si
x tiende a +![]() entonces ax tiende a
+
entonces ax tiende a
+![]() .
.
Ejemplo 5. Gráfica de y = 2x
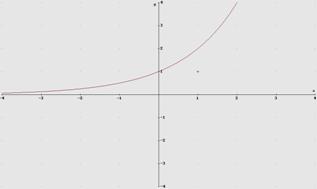
Ejercicio 9. Estudiar el caso 0<a<1
Ejemplo 5 bis. Gráfica de ![]()
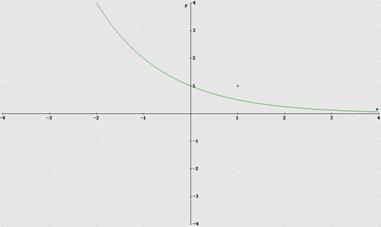
Ejercicio 10. Calcular la gráfica de la función ![]()
Propiedades de las funciones exponenciales (repasarlas)
Aplicaciones
Gran cantidad de fenómenos siguen un comportamiento que puede ser descrito por funciones exponenciales. Veremos dos de ellos:
Evolución de la población mundial
Ejemplo 6. Se estima que la población mundial aumenta un 1,8% anualmente. En Enero de 1983 la población era de 4677 millones. a) Suponiendo que la tasa de variación es constante, ¿ Cuál sería la población en el año 2000?. b) ¿A partir de que año se puede estimar que, en estas condiciones, sobrepasará los 10000 millones?
Solución
La función que nos da la población en función del tiempo es:
y = 4677.(1,018)x (y en millones y x en años)
a) 2000 -1983=17, luego y = 4677(1, 018)17 = 6334, 02 millones
b) Se tiene que cumplir que y> 10000, comprobar que en el año 2026.
La desintegración radiactiva
Ejercicio 11. Se llama vida media de una sustancia radiactiva al tiempo que tarda en reducir su masa a la mitad por el proceso de desintegración.
Sabiendo que la vida media del radio es de 1620 años, y que en una roca se encuentran 10 gr. de radio averiguar:
a) La cantidad de radio que habrá en esa roca en el futuro, en función del tiempo.
b) La cantidad de radio que había en esa roca hace 2500 años. (Sol. 29,144)
- Funciones logarítmicas
Son las funciones inversas de las funciones exponenciales y se designan y =logax (a>0).
Entonces logax =y sí y sólo sí x =ay.
Su dominio es R +, su recorrido es R. Todas pasan por (1, 0).
Si a>1
Son crecientes en todo su dominio
Si x>1, loga x >0
 Si x<1, loga x<0
Si x<1, loga x<0
Si
x tiende a 0 loga x tiende a +![]()
Ejemplo 7. Gráfica del logaritmo neperiano de x, y =ln x
Ejercicio 12. Estudiar los casos 0<a<1
Propiedades de los logaritmos (repasarlas)
Ejercicio 13. Resolver el apartado b) del ejercicio 10 usando logaritmos.
- Funciones trigonométricas
son funciones periódicas (repasar las gráficas de, al menos, el seno coseno y la tangente.
Nota. En las funciones trigonométricas la variable x siempre va expresada en radianes,
Ejemplo 8. La gráfica de la función seno:
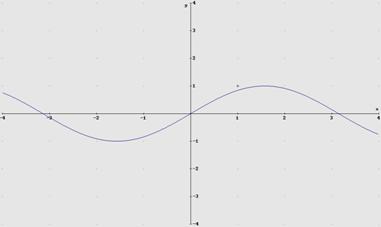
- Funciones definidas a trozos
Son funciones a las que corresponde distinta expresión matemática, según el punto del dominio que se considere:
Ejemplos importantes
La
función valor absoluto, ![]() =
= ![]()
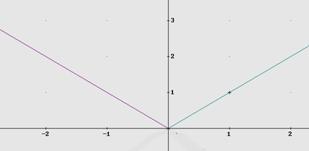
La función signo (o función de Heavyside), que asocia a cada número su signo se define así.
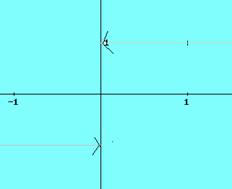
![]()
Observación: La función signo también se
puede definir de la siguiente forma: ![]() .
.
Ejercicio 14. Haz la gráfica. de la función parte entera de x, E(x)=[x].
Ejercicios: Límites de una función en un punto. Límites infinitos. Indeterminaciones
Estudia si tienen límite las siguientes funciones, en los puntos que se indican:
1. en x =0 y x =1

Solución
En x =0 la función tiene límite y vale -2
En x =1 no existe el límite, pues los límites laterales no coinciden.
2.
![]() en
x =2
en
x =2
3.
![]()
4.
![]()
5. ![]() x.
x.
Solución: ![]() x =
x = ![]()
6 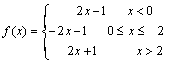 ; en
x =0 y x =2
; en
x =0 y x =2
Calcula las asíntotas de las siguientes funciones y sitúa la curva con respecto a ellas:
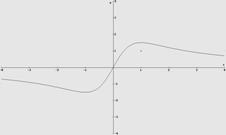 1.
1. ![]()
Solución.
Verticales no tiene pues el dominio es todo R
Horizontales
![]() , y =0 , no hay oblicuas
, y =0 , no hay oblicuas
2. ![]()
3. ![]()
4. y =e-x
5. y =ln (x2-1)
*Calcula los siguientes límites, caso de que existan:
1. ![]()
Solución: Es
una indeterminación del tipo ![]() . Por tanto se simplifica la fracción y
se vuelve a calcular el límite:
. Por tanto se simplifica la fracción y
se vuelve a calcular el límite:
![]()
![]() =
=![]()
2. ![]()
3. ![]()
4. ![]()
5.![]()
Solución es
una indeterminación del tipo ![]()
![]()
![]() =
=
![]() =
=![]()
6. ![]()
7. ![]()
8. 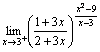
9.![]()
Solución.
Es una
indeterminación del tipo ![]()
![]() =
=![]()
10. 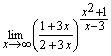
11.
![]() =
=![]() =0
=0
6. Funciones continuas
 De una manera
intuitiva se puede decir que una función es continua cuando su gráfica se puede
dibujar sin levantar el lápiz del papel.
De una manera
intuitiva se puede decir que una función es continua cuando su gráfica se puede
dibujar sin levantar el lápiz del papel.
De una manera “más formal”y teniendo en cuenta la definición de límite:
Definición. Una función es continua en un punto a si se verifican tres condiciones:
1ª) a pertenece al dominio de f.
2ª) existe el límite de f(x) cuando x tiende hacia a.
3ª) dicho límite vale f(x)
Esta definición puede resumirse diciendo: f es continua en a sí y sólo sí.

![]()
Ejemplo
9. La función f(x) = 1/x es continua en el abierto (0, ![]() , pero no en
[0,
, pero no en
[0, ![]() ,
pues en 0 no está definida.
,
pues en 0 no está definida.
Operaciones con funciones continuas
Sean f y g dos funciones continuas en a:
a) f +g y f.g son continuas en a.
b) si además g(a)¹0, entonces f/g es continua en a.
Si g es continua en a y f continua en g(a) entonces fog es continua en a.
Continuidad en un intervalo
Si f es continua en x para todo x de (a, b) entonces se dice que f es continua en (a, b )
Una función es continua en un intervalo [a, b] cuando lo es en (a, b) y existen:
![]() y
y ![]()
Ejemplos de funciones continuas
1º Toda función polinómica es continua en R
2º Las funciones racionales son continuas salvo en los puntos que anulan al denominador.
3º Las funciones seno, coseno, exponenciales y logarítmicas son continua en sus dominios respectivos.
Propiedades de las funciones continuas(2 intuitivas)
- Ceros de las funciones continuas (T. Bolzano)
- Teoremas de los valores intermedios
-Acotación de intervalos cerrados.
Teorema de Weiertrars
*Ejercicio 15. Demuestra que la ecuación x3 +5x-2 tiene al menos una solución real e indica un l intervalo al que pertenezca
Funciones discontinuas tipos
Cuando una función no sea continua se dirá discontinua y esto puede ocurrir de varias formas.
Discontinuidad evitable
Una función tiene una discontinuidad evitable, en un punto a, si existe límite de la función en el punto, a, pero o no coincide con el valor de la función, f(a), o a no pertenece al dominio de f. Es decir, verifica 2ª pero no se cumple 1º o 3ª.
Ejemplo 10. La función ![]() es
discontinua en x =3, pues la función no existe en 3, pero sí existe el límite
en ese punto (comprobarlo) por lo tanto la discontinuidad es evitable
es
discontinua en x =3, pues la función no existe en 3, pero sí existe el límite
en ese punto (comprobarlo) por lo tanto la discontinuidad es evitable
Discontinuidad de 1º especie (o de salto)
Si existen los límites laterales en un punto, pero no coinciden, la discontinuidad se llama de salto. El salto (finito) es la diferencia entre estos valores (en valor absoluto). Cuando uno de los límites laterales de infinito se trata de una discontinuidad de salto infinito.
Ejemplo 11. a) la función
signo ![]() en x = 0 presenta una
discontinuidad de salto 2, pues
en x = 0 presenta una
discontinuidad de salto 2, pues
![]()
![]()
y el salto es 1-(-1)=2.
b) La función f(x) = 1/x es discontinua en 0 de salto infinito.
 |
Discontinuidades esenciales de 2ª especie
Si no existe alguno de los límites laterales la discontinuidad se dice de 2ª especie, o esencial.
Ejemplo 12. ![]() tiene
una discontinuidad esencial en 0.
tiene
una discontinuidad esencial en 0.
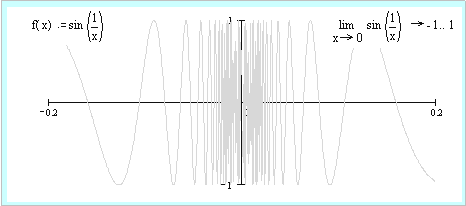 |
es decir no existen ni los límites laterales pues “oscilan entre 1 y -1”
Ejercicios de Continuidad
1.Estudia la continuidad de las siguientes funciones:
a)
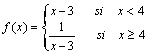
b)
![]()
2.Dada la función 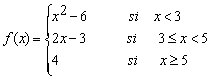
Estudia los puntos en que f es discontinua y clasifica las discontinuidades que presenten. Representación gráfica.
3. Dada la función:
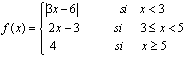
Estudia los puntos en que f es discontinua y clasifica las discontinuidades que presenten.
4. Calcula el valor de k para que las siguientes funciones sean continuas:
a) 
b) ![]()
![]()
Ejercicios y problemas propuestos
1. Calcula el dominio de:
a)
![]() ;
b) f(x) =
;
b) f(x) = ![]() ; c)
; c) ![]() .
.
2. Estudiar la simetría de las funciones siguientes:
a)
f(x) = - 3x2 + 1; b) f(x) = x3 - 3x; c) ![]() .
.
3. Estudiar si están o no acotadas las siguientes funciones:
a)
f(x) = x2 - 5 ; b) ![]() ; c) f(x) =
; c) f(x) = ![]() .
.
4. Calcula la inversa de ![]() . Comprueba el
resultado
. Comprueba el
resultado
5. Conocida la gráfica de f(x)= sen x dibuja la gráfica de g(x)=1+ sen x
6. Calcula el intervalo en que f(x) = ex(x2-3x+2) es negativa.
7. Dibuja la gráfica de :
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
8. Dadas las funciones f(x)= 4x-3 y g(x)=x2 determinar fof y gof.. Representar gráficamente esta última indicando en que puntos alcanza los valores extremos.
9. Representa una función que verifique las siguientes condiciones:
![]()
![]() ,
, ![]() ,
, ![]() y
y
![]()
10. Calcula los siguientes límites
a) ![]() b)
b) ![]() ;c)
;c)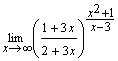
11. Dada la función f(x)= a + ln(x +b) se pide:
a) Dar el dominio y el rango de la función si b =10 y a = 106
b) Calcular el valor de a sí, siendo b = -9, se desea que f(10)=100.
12. En una empresa se hacen montajes en cadena. El número de montajes realizados por un aprendiz depende de los días de aprendizaje, según la función
![]() , t en
días.
, t en
días.
Representa la función sabiendo que el periodo de aprendizaje es de 30 días. ¿Cuántos montajes realiza el primer día?¿y el 30?
¿Qué ocurriría con el número de montajes si nunca se acabara el aprendizaje?
13. Un capital de 12000 € está colocado al 3% fijo anual. Calcula la expresión que nos da el capital acumulado al cabo de t años.
14. Dada la función 
a) Representación gráfica.
b) Clasifica los puntos de discontinuidad.
Se completa el tema con los ejercicios resueltos relativos al tema de funciones en los siguientes enlaces:
OBSERVACIÓN. Esta página está pensada, sobre todo, para matemáticas aplicadas a las ciencias sociales, si necesitas más ejercicios o más nivel en los temas de Funciones en el Bachillerato visita el enlace Matemáticas en el bachillerato
Si necesitas otros temas, visita la página inicial de esta Web donde encontrarás un ÍNDICE de todos los temas.
Cuaderno de actividades 2º bachillerato MCS