ESTUDIO DE LA CONTINUIDAD DE  FUNCIONES

1. Dada la función F(x)=

 

a)     hallar los puntos de discontinuidad

b)    Si existe alguno, hallar los limites laterales y el salto de discontinuidad

c)     Determinar si se puede completar el dominio de la función de modo que sea continua en toda la recta

Solución

a)     El único punto en que es discontinua es en x = 2, que anula el denominador.

b)      Lo límites laterales:

        

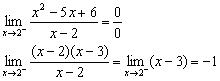
Análogamente cuando x tiende a 2⁺, da también -1

         Como los límites laterales coinciden la discontinuidad es evitable.

      c)  El dominio de la función F es R-Como la discontinuidad e evitable sí se puede “completar” el dominio con el 2, definiéndola en ese punto con el valor de dicho límite. Es decir:

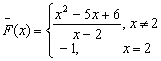   es continua

2.  Dada la función  F(x)= , se pide:

 

a)     hallar los puntos de discontinuidad

b)    Si existe alguno, hallar los limites laterales y el salto de discontinuidad

c)     Determinar si se puede completar el dominio de la función de modo que sea continua en toda la recta

Solución

a)     Como es un cociente de polinomios es discontinua en los puntos que anulan al denominador.

     x²-4x+4=0, x =2  (raíz doble) es el único punto de discontinuidad

    

b)    Los límites laterales:

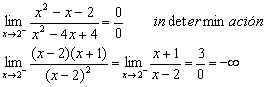        (ya que x-2<0, para valores menores que 2)

 

          

 

(ya que x-2>0 para valores mayores que 2)

Es una discontinuidad de primero especie o de salto. El salto es infinito

c)     Por ser una discontinuidad de salto no se puede definir en x =2 (no se puede completar el dominio) de modo que se continua (esto sólo se puede hacer en las discontinuidades del tipo evitable) 

 

Continuará