3ª Parte: Ecuaciones y sistemas
Igualdades, identidades, ecuaciones
Una igualdad, (=), es una relación de equivalencia[1] entre dos expresiones, numéricas o literales, que se cumple para algún, alguno o todos los valores. Cada una de las expresiones recibe el nombre de miembro.
|
igualdad
una expresión = otra expresión
primer miembro segundo miembro
|
· Si la igualdad se cumple entre números se denomina identidad numérica.
Ejemplo 1: 2 +4 +5 = 1 +10
· Una identidad literal es una igualdad que se cumple para todos los valores.
Ejemplo 2: Las Identidades Notables
Cuadrado
de una suma 
Cuadrado de una diferencia 
Diferencia de cuadrados 
· Cuando la igualdad se convierte en identidad numérica sólo para determinados valores se la llama ecuación. A las letras se les llama indeterminadas o incógnitas.
Ejemplo 3: a) 3x+2 =0 es una ecuación con una incógnita.; b)3x +2y =1 es una ecuación con dos incógnitas.
Al valor, o valores, que convierten la ecuación en identidad numérica se les llama solución (o raíz) de la misma.
Ejemplo 4. Una solución de la ecuación del ejemplo 3 es x =-2/3 .
Ejercicio 1. Encuentra 2 soluciones de la ecuación 3x-2y-1=0
Resolver una ecuación en encontrar todas su soluciones o llegar a la conclusión de que no tiene ninguna.
Ejemplo 5. a) x2-1=0 tiene dos soluciones, x =1 y x =-1
b) x2 + 1=0 es una ecuación sin soluciones en R.
c) 2x +3y = 0 tiene infinitas soluciones, (0,0), (-3,2), (3, -2)....
Ecuaciones equivalentes
Dos ecuaciones son equivalentes cuando admiten la mismas soluciones. Se cumple:
v Si se suma o resta un mismo número a los dos miembros de una ecuación, se obtiene una ecuación equivalente a la primera.
v Si se multiplican o dividen los dos miembros de una ecuación por un mismo número distinto de cero se obtiene una ecuación equivalente a la primera.
Trasposición de términos.
Aplicando las reglas anteriores deducimos dos reglas prácticas:
Ø Si un número aparece en un miembro sumando, se le puede pasar al otro miembro restando. Si esta restando pasará sumando.
Ø De igual manera si está multiplicando pasa dividiendo y al revés.
Esto se llama trasponer términos.
Ejemplo 6: La ecuación 5x - 1 = 2x -3 se puede escribir 3x + 2 = 0, trasponiendo términos.
Nota : El segundo miembro de la ecuación se puede considerar siempre que es 0.
Ecuaciones de primer grado
La forma general de esta ecuación
es a x +b =0 con a
0
Trasponiendo y dividiendo por a
se llega a 
.
Solución que siempre existe y es única.
Ejemplo 7. a) 3x +2 =0 Þ 
b) 7x + 2 = 2x -3 , si trasponemos términos, nos queda 7x –2x = -2 –3
Luego 5x = -5 de donde x = -1
Ecuaciones de segundo grado
La forma general de una ecuación de 2º grado es: 
,
donde a
La solución de esta ecuación general viene dada por la fórmula:
Ejemplo 8. 
=
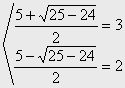
Observación. A D =
se llama discriminante de la ecuación de 2º y se
verifica:
Si D>0 la ecuación tiene dos soluciones conjugadas
Si D =0 la ecuación tiene una única solución (doble)
Si D <0 la ecuación no tiene ninguna solución real.
Ecuaciones incompletas
- Si c =0 la ecuación se reduce a
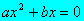y
sacando factor común x se tiene:
x(ax +b) =0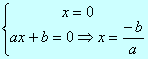
Este tipo de ecuación siempre tiene dos soluciones.
Ejemplo 9. 3x2-5x=0 x(3x-5)=0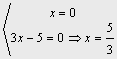
- Si b =0 la ecuación
queda
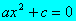de donde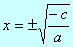 
Puede tener dos soluciones opuestas o ninguna solución, dependiendo de que
El radicando sea o no positivo.
Ejemplo 10. 2 x2-
=0; 2 x2=Þ 
(dos
soluciones)
Ejemplo 11. 3x2+1 =0 
(no
tiene ninguna solución)
Resolución “práctica” de una ecuación
Lo estudiamos con un ejemplo
Ejemplo 12. 
Para resolver la ecuación seguiremos el siguiente orden.
1º Quitar denominadores
Al multiplicar los dos miembros de una ecuación por el mínimo común múltiplo de sus denominadores, se obtiene otra ecuación equivalente a la primera, pero sin denominadores.
Multiplicamos los dos miembros de la igualdad por 6, que es el m.c.m. de los denominadores.
Nos queda 3(2x-3) -2(5x-1) =6
2º Quitar paréntesis
Se efectuarán las operaciones indicadas, utilizando la propiedad distributiva.
Quitando paréntesis 6x-9 –10x+2=6
3º Trasposición de términos
Se disponen todos los términos que llevan x en un miembro y los demás en el otro.
Trasponiendo términos 6x –10x = 9 - 2 + 6
4º Reducción de términos semejantes
De este modo cada miembro de la ecuación queda con un solo término:
-4x = 13
5º. Despejar la incógnita
Se dividirá ambos miembros
por el coeficiente de la incógnita (se puede hacer siempre que sea a0)
Observación. Dependiendo de la ecuación a resolver puede ocurrir que alguno de los pasos sea innecesario, se omite y se pasa al siguiente.
EJERCICIOS PARA PRACTICAR
Ecuaciones de primer grado
Resuelve
1) 
2)
3) 
4) 
5) 
7) 
8) 
9) 
Solución.
Multiplicamos los dos miembros por 8 (es el m.c.m. de los denominadores)
(2x-4)2 = 40 +4x(x +1)
4x2 –16x +16 = 40 + 4x2 +4x
4x2 –16x +16 =40 +4x2 +4x
Reduciendo términos semejantes:
16x-4x= 40- 16 -20x =24 
=
-1,2
10) 
Ecuaciones de segundo grado
Resuelve las siguiente ecuaciones indicando si son completas o no:
1) 3x2+ 2x=0
2) 5x2-3=0
3) x2-4x+2=0
4) 2x2+ x-1=0
5) 3 x2-
=0 Þ 3x2 = Þ x2=
Þ x =
6) –x2 + 4 =0
8) 4x2 –4x +1 =0
9) –x2 +6x-5=0
10) –6x2 +5x-1=0
11) (5x-4)(2x+3) =5
12) 30 + 9x – 3x2 =0
13)
Solución.
Multiplicamos por el M.C.M de los denominadores, que es 2(2 +x):
(2 +x)(2-x) +4.2 =2(2 +x)
4 –x2 +8 =4 + 2x,
agrupando términos y organizando la ecuación
0 = x2 +2x
–8 Þ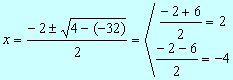 
14) 
15) 
16) 
Aplicaciones de las ecuaciones de 2º grado
Ø Descomposición en factores del trinomio de 2º grado.
Ejemplo 13.La ecuación x2 –5x +6= 0 tiene dos raíces r1=3 y r2= 2 (comprobarlo).
Entonces se puede descomponer en producto de (x-3) por (x-2). Es decir:
x2 –5x +6 = (x-3)(x-2).
Ejercicios
Determina los factores de los siguientes trinomios de 2º grado
1) x2-16
2) x2-13x+36
3) 4-x2
4) 2x2+17+21
5) 2x2-5x+7
6) 3x2- 0,75
7) –x2 +5x-6
4) Solución
=
Luego 2x2+17+21= 2(x +1)(x +7)
Ø Resolución de ecuaciones irracionales.
Ejemplo 14. 
Se procede de la forma siguiente:
1) Se aísla la raíz:
2) Se elevan al cuadrado ambos miembros de la igualdad:
4(x-1)=(4-x)2 Þ 4x-4 = 16-8x +x2
3) Se resuelve a ecuación de 2º grado que resulta
x2-12x +20 =0 x =10 y x =2 (comprobarlo)
4) Se comprueban las soluciones
Si x =10
16 - 4= 0 Falso, no es
solución
Si x =2
4 - 4=0 Cierto, si es
solución.
Ejercicios
Resuelve las siguientes ecuaciones y comprueba las soluciones:
1) 
2) 
3) 
4) 
5) 
6) 
Solución.
Aislamos una de las raíces: 
Elevamos al cuadrado (
Volvemos a aislar la raíz que nos queda
Elevamos al cuadrado
144(2x-1)=x2 +62x+961
288x -144 = x2 +62x +961
Es decir:
x2 –226x +1105 =0
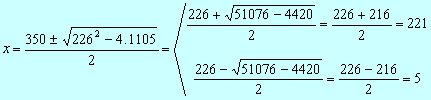
Comprobamos las soluciones:
x =221 no es solución pues
x =5 sí es solución
3=3
7) 
Ø Ecuaciones bicuadradas
Ejemplo 15. La ecuación x4 – 5x2 +6=0 es bicuadrada (es de 4º grado sin potencias impares).
Para resolverla se procede así:
Se hace un cambio de incógnita
x2= y
con lo cual x4 = y2
Sustituyendo en la ecuación: y2-5y+6=0
que sí es de 2º grado y podemos aplicar la fórmula: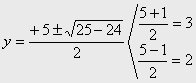 
Sustituyendo los valores en la
expresión x2= y , x =
obtenemos:
y
En este caso la ecuación tiene 4 soluciones.
Ejercicios
Resuelve:
1) x4 –3x2+2
2) x4-13x2+36
3) x4-1
4) x4+ 4x2 =0
Solución.
Como es incompleta, .al igual que en las de segundo grado, sacamos factor común
x2(x2 +4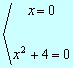) =0
que
tiene sólo la solución (doble) x =0
5) x4-9x2=0
6) 3x4 –5x2+2=0
7) x4+ x2+1=0
8) 
El tema continua en el siguiente enlace Sistemas
El tema completo se repasa y amplia en Álgebra
Cuaderno de actividades 3º ESO
