Cuaderno de Actividades 3º ESO
1ª PARTE: OPERACIONES CON NÚMEROS[C1]
A) ENTEROS
Realiza las siguientes operaciones:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) (16) : (-2)+4(3-1)+9 = -8 + 4.2+9 = - 8 +8 +9 =9
7) (-12): (3)+3.5-6(8-3)
8) 15: [(-12): 4]+5
9) –3+(5-3.7)+(3)2
10) (-2)3+(5.6-8)-2
11)
![]()
12) 4-3(-2)3-5{(-3)2(-1)5+7.2-3(7-2)+1}
11. Solución Seguimos la jerarquía de las operaciones y uso de paréntesis:
Efectuamos los paréntesis 2(-1)4+(-2)3+82-3(2)
“ las potencias 2.1+(-8)+64-3(8)
“ los productos 2-8+64-24
por último las sumas y restas 66-32=34
B) RACIONALES: FRACCIONES Y DECIMALES
a) Calcula:
1) ![]() de
120
de
120
2) ![]() de
3600
de
3600
3) La
mitad de ![]()
4) La tercera parte de ![]() .
Solución
.
Solución ![]()
5) La mitad de la quinta parte de –15
6)
Cuánto dinero tengo si los ![]() de éste son 34 euros.
de éste son 34 euros.
Dos fracciones son equivalentes si producto de extremos es igual a productos de medios.
Si multiplicamos, o dividimos, el numerador y el denominador de una fracción por un mismo número obtenemos una fracción equivalente.
7)
Tres fracciones equivalentes a: ![]() ,
, ![]() .
.
8) Calcula x, en cada caso, para que las igualdades sean ciertas:
![]() ;
; ![]() ;
; ![]()
Solución. Como son fracciones equivalentes, x =3.7=21; x =7.5=35; x = 5.3=15
9) Calcula el 20% de 375 euros.
b) Reduce a común denominador[1]las siguientes fracciones
1) ![]()
2) ![]()
3) ![]()
4) ![]() y
y![]()
5)![]()
3. Solución. El m.c.m. (3, 5, 2)=30.
![]()
![]()
![]()
Es decir: 10/30; 12/30 y 45/30
c) Ordena de menor a mayor las siguientes fracciones
1) ![]()
2) ![]() ,
,![]()
3) ![]()
4) ![]()
1) Una vez que hemos encontrado fracciones con igual denominador
equivalentes, ordenamos los numeradores: 10/30; 12/30 y 45/30 es decir: ![]()
d) Simplifica las siguientes fracciones
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
5)
Solución. ![]()
Operaciones con fracciones
Suma ![]()
Caso particular: si tienen igual denominador se suman los numeradores y se pone el denominador común. Esto da lugar al método de reducción a común denominador (se coge el m. c. m) para la suma.
Producto ![]()
Cociente ![]()
e) Calcula:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9)
![]()
10) 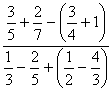
9. Solución.
![]() =
=![]()
![]()
f) Encuentra la fracción generatriz (de la que proceden esos números) de los siguientes números:
1)
0,03 2)![]()
3)
![]() 4)
4)
![]()
3) Solución.
Si hacemos N=![]() 10N=
10N=![]() 100N=
100N=![]()
Restando los dos números que tienen el mismo periodo, éste se “va”:
100N-10N=![]() -
-![]() 90N
=112ÞN =
90N
=112ÞN =![]()
g) Calcula pasando a fracción:
1) ![]()
2) ![]()
3)![]()
h) Representa los siguientes números racionales:
2/3; -3; 7/5; -3/4, 12/8
![]()
![]()
![]()
![]()
![]()
1/3 2/3
i) Escribe en forma decimal o fraccionaria las siguientes expresiones:
1) Dos quintos.
2) Tres de cada cinco.
3) Mitad de cuarto.
4) Dos partes por mil.
5) Tres partes de agua y dos de alcohol.
6) Escala 1 a 200000. Solución1:200000
se expresa ![]()
7) 13 décimas.
8) 234 centésimas.
9) Una millonésima.
C) NÚMEROS APROXIMADOS. ERRORES
a) Di cuáles de los siguientes números son racionales y cuales no lo son:
1) ![]() 2)
2)
![]() ;
;
3) ![]() ;
4)
;
4) ![]() ;
;
5) ![]() 6)
6)
![]()
7) 3,56565656...... 8) 3,141592.....
9) 0,30300300030000.... no es racional las cifras decimales no se repiten, es decir no es periódico
10) –3,45454545.....
b) Calcula, sin usar la calculadora, las siguientes raíces exactas:
1) ![]() ; 2)
; 2)
![]() ;
;
3) ![]() 4)
4)
![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8)
![]()
6) Solución. ![]() =
=![]()
c) Calcula una aproximación decimal de los siguientes números no racionales:
1) ![]()
2)
![]() ;
;
3) ![]()
4) ![]()
2) Solución. Utilizamos la tecla x y para hallar potencias con una calculadora.
62=36; 72=49, luego está entre 6 y 7
6,82=46,24;
6,92=47,61 Con un decimal la aproximación seria ![]() =6,8
=6,8
6,842=46,78;
6,852=46,92; ,6,862=47,05. Luego ![]() =6,85
con dos decimales exactos.
=6,85
con dos decimales exactos.
Siguiendo el proceso se podría calcular con el grado de aproximación que deseáramos.
d) Halla las raíces posibles y di cuáles son imposibles y por qué:
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)![]()
5) ![]() no existe pues el índice
es par y el radicando negativo
no existe pues el índice
es par y el radicando negativo
e) Escribe tres aproximaciones decimales de los números:
1) ![]() 2)
2)
![]()
f)
Calcula la
cota del error que se comete al sustituir el número ![]() por:
por:
1) 3,14 2) 3,142 3) 3,1415
2) Solución. Tiene tres cifras decimales exactas, luego el error q se comete es menor que 10-3
g) Escribe las aproximaciones
por defecto del número ![]() ,
con la mínimas cifras para que el error cometido sea menor que:
,
con la mínimas cifras para que el error cometido sea menor que:
1) una décima.
2) una milésima
h) Calcula el lado de un cuadrado, cuya área es 1500 m2 , con un error menor que una centésima.
D) POTENCIAS
Propiedades de las potencias
1.![]()
2. ![]() (caso
especial n =0, queda
(caso
especial n =0, queda ![]() )
)
3. ![]()
4. ![]()
5. ![]()
a) Hallar el valor de las siguientes potencias:
1) (-3)3 2) 5-2
3) ![]() 4)
4)
![]()
5) (-3)2.3-3 6) 52.5-3.57.5-4
7) ![]() 8)
8) ![]()
8) Solución. ![]() =
=![]() =3-8.2-1
=3-8.2-1
b) Escribe en forma de potencia de una sola base:
1)
625 2) 128 3) ![]()
4)
![]() 5)
5) ![]()
![]()
5) ![]() =
=![]()
c) Expresa como potencia única:
1)
(5-3.52)-6 2) ![]()
3)
![]() 4)
4) ![]()
4)
Solución. ![]()
![]()
d) Simplifica:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
3) Solución. Primero reducimos las potencias a bases positivas
![]()
![]() =+
=+![]() =782-75-2
=782-75-2
e) Escribe como potencia de 10
1) 0,00001= 10-5
2) una millonésima
3) 1000000000
f) Indica el orden de magnitud [2]de las siguientes medidas:
1) El volumen de la Tierra: 1,0807.1021m3
2) La masa del Sol: 1,98.1030kg
3) La masa de un electrón: 1,67.10-27kg
g) Escribe con notación científica::
1) 310000000000
2) 0,00000023=2,3.10-7
3) 1540,23
4) El número de moléculas que hay en un gramo de hidrógeno: 301000000000000000000000= 3,01.1023
5) La longitud de un paramecio: 0,000025 m
h) Expresa en forma decimal:
1) 3,23.10-7
2) 1,75.108
3) La masa de un electrón: 1,67.10-27kg
4) El precio de una casa: 3,24.107 =32400000
5) El volumen de la Tierra: 1,0807.1021m3
6) La masa del Sol: 1,98.1030kg
E) RADICALES (Iniciación)
a) Completa siguiendo el modelo:
![]()
1)
![]()
2)
![]() =
=
3)
![]() =
=
b) Extrae factores del radical siguiendo el modelo:
![]()
1)
![]()
2)
![]()
3)
![]()
4) ![]()
c) Suma las expresiones con radicales (que puedas):
![]() =
=
![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5)
![]()
6)
![]()
7)
![]()
8) ![]()
Ayuda. Recuerda que los radicales solo se pueden sumar cuando son semejantes[C2].
**d) Opera los siguientes radicales y/o simplifica cuando sea posible:
1)
![]() 2)
2) ![]()
3)
![]() 4)
4) ![]()
5)
![]() 6)
6) ![]()
7)
![]()
![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
3) Solución.
Se reducen a índice común y después se multiplican los radicandos.
m.c.m(2,3)=6 ![]() =
=![]() =
=![]()
![]()
**e) Representa en la recta real los números:
1)![]() 2)
2) ![]()
3)![]() 4)
4)
![]()
2) Solución . Utilizamos el Teorema de Pitágoras. 5 = 12+22

1 ![]() es la diagonal del
triángulo, con un compás de origen 0 se obtiene donde está situado
es la diagonal del
triángulo, con un compás de origen 0 se obtiene donde está situado
2 ![]() .
.
 Problemas[C3]
Problemas[C3]
1.Algunos gorriones estaban posados en dos árboles, teniendo cada árbol la misma cantidad de gorriones. Dos gorriones echan a volar yendo del primer árbol al segundo. ¿cuántos gorriones más que el primer árbol tiene ahora el segundo árbol?
2. Primero un globo asciende 200 m. desde el suelo, luego se mueve 100 m. hacia el este, y después desciende 100 m. Entonces recorre 50 m. hacia el este y finalmente baja en recto hasta el suelo. ¿A qué distancia se encuentra el globo del punto de partida?
3. En una carrera atlética Juan aventaja a Pedro en 10 m., Tomás aventaja en 4 m a Jaime y Jaime aventaja en 3 m. a Pedro. ¿Cuántos m. de ventaja le lleva Juan a Tomás?.
4. Anteayer tenía 17 años y el año que vienen cumpliré 20 años. ¿Cómo es posible?
5. Una pista de carreras de atletismo se divide en tres tramos desiguales. La longitud total de la pista es 450 m. La longitud de los tramos primero y segundo juntos es 350 m. La longitud de los tramos segundo y tercero juntos es 250 m. ¿Cuál es la longitud de cada tramo?
6. Tengo tantas hermanas como hermanos, pero mis hermanas tienen la mitad de hermanas que de hermanos. ¿Cuántos somos?
7. Una sierra en un aserradero corta largos troncos, de 16 m de longitud, en troncos cortos, de 2 m. de longitud. Si cada corte se hace en dos minutos, Cuánto tiempo se necesitará para que la sierra produzca los ocho troncos cortos a partir de un tronco largo.
8. Un bidón lleno de queroseno pesa 8 Kg. Se derrama la mitad del queroseno, después de lo cual bidón y contenido pesan 4 Kg. y medio. Determinar el peso del bidón vacío.
9. Un pasajero al llegar a la mitad de su viaje cae dormido. Cuando despierta, aún tiene que recorrer la mitad de la distancia que ha hecho mientras dormía ¿Qué parte del total del camino ha estado durmiendo?.
11. Partiendo de un punto P, un oso camina un Km. hacia el sur. Cambia entonces de dirección y recorre un Km. hacia el este. después dando la vuelta de nuevo a la izquierda, recorre un Km. hacía el norte para llegar exactamente al punto de partida P. ¿De qué color es el oso?
12. Diez ciruelas pesan tanto como tres albaricoques y un mango. Seis ciruelas y un albaricoque pesan lo mismo que un mango. ¿Cuántas ciruelas equilibrarían una balanza que tiene en un lado un mango.
13. Tres amigos coinciden en un restaurante. Comentan que todos van habitualmente. Uno de ellos va cada 5 días, otro cada 6 y el otro cada 9. ¿al cabo de cuántos días volverán a encontrarse?.
14. En una cooperativa tienen 360 litros de un cierto tipo de aceite y 225 litros de otro tipo. Quieren envasar el aceite con el menor número posible de garrafas iguales ¿Qué capacidad tendrá cada garrafa?
15. La masa de un virus es de 10-21kg, la de un hombre, 70kg, y la de la Tierra 5,9 x 1024kg. Calcula la relación entre la masa de un hombre y un virus, y la de la Tierra y un hombre. ¿Cómo son estas relaciones?
16. Al principio, el precio de un Kg. de azúcar era tres veces el precio de un Kg. de sal. Después, el precio de un Kg. de sal aumentó en la mitad de su anterior precio, sin que cambiara el precio del azúcar. Si el precio de la sal es ahora 30pts. por Kg., ¿cuál es ahora el precio del azúcar por Kg.
17. Una molécula de agua, H2O, está compuesta por dos átomos de hidrógeno (H) y uno de oxígeno (O). Sabiendo que el peso del hidrógeno es 1 y el del oxígeno 16 calcula el porcentaje de peso que corresponde a cada uno.
18. El precio de un artículo sin IVA es de 750 euros. Si he pagado 840euros. ¿Qué porcentaje de IVA me han cobrado?
19. Un cobrador se queda con el 0,5% de la cantidad recaudada. Si le ha correspondido 6250 euros, ¿cuánto ha cobrado?
20. El precio de la gasolina subió en Enero 3%. En Febrero subió un 5% y en Marzo bajó un 4%.¿ Cuál fue el porcentaje de variación del precio en este trimestre?.
21. Se mezclan 20litros de aceite de oliva de 2,2 euros el litro, con 13litros de aceite de semillas a 1,3 euros el litro. ¿A cuánto sale el litro de la mezcla?
22. Para la fabricación de queso se mezcla un 60% de leche de vaca con un 40% de leche de oveja. El precio de la leche de vaca es de 0,85 euros el litro y el de la leche de oveja es de 1,2 euros el litro. Para fabricar un queso se necesitan 8 litros de leche. ¿A qué precio saldrá la mezcla?
23. Reparte 6000 euros en partes proporcionales a 2, 3 y 5.
24 Tres socios pusieron 20 millones, 30 millones y 60 millones, respectivamente, para crear una empresa. A) ¿Qué parte de las ganancias corresponderá a cada uno?. Si las ganancias del primer año fueron 7590000. ¿Cuánto corresponderá a cada uno?
25. Un grifo llena un depósito en 2 horas, y otro grifo lo llena en tres horas. ¿Cuánto tardará en llenarse el depósito si se abren ambos grifos a la vez?
26. Tres grifos aportan caudales de 2 l/s, 3 l/s y 5 l/s, respectivamente. Se abren los tres a la vez para llenar un balsa.
a) ¿Qué fracción de la misma habrá aportado cada uno?
b) Si la balsa tiene una capacidad de 6000 litros qué volumen de agua ha manado de cada grifo?
27. Un grifo arroja 70l de agua por minuto y otro arroja 50l por minuto. ¿Cuánto tiempo tardarán en llenar entre los dos un depósito de 360l?
28. Tres personas trabajando 8 horas diarias hacen un trabajo en 15 días. ¿Cuántos días tardarán en hacer el mismo trabajo cinco personas en jornadas de 9 horas?
29. . Un camión cubre el trayecto entre dos ciudades en 9 horas y un coche hace el recorrido contrario en 6 horas. Si salen simultáneamente, cada uno de una de las poblaciones. ¿Cuánto tardarán en cruzarse?
30. Calcula la diagonal de un cuadrado de lado 5
Soluciones de los problemas seleccionados
2. Solución 100
50
A 150 B
A 150 metros
4. Solución.
Estamos a 1 de enero y nací el 31 de diciembre
6. Solución.
4 hermanos y 3 hermanas
![]()
![]() 8. Solución.
8. Solución.
![]() .
.
8kg 4,5kg
El líquido derramado pesará 8 - 4,5 = 3,5
El líquido en total pesará 7kg, luego el bidón vacío pesa 1kg.
11. Solución.
Blanco , por que tiene que estar en el polo norte para que pase eso.
 P
P
 P P
P P
1 km. 1 km.
1 km.
13. Solución.
Se encontrán en un múltiplo común a todos.
m.c.m.(5,6, 9, )=90
Se encuentran a los 90 días
16. Solución
30 = precio anterior + 1/2 del precio anterior
30= 3/2 del precio anterior Þ
precio anterior de la sal = 30.2/3 = 20
precio del azúcar 3.20 = 60pts
18. Solución.
Aplicamos en concepto de índice de variación.
Se tiene CF = CI. IV, luego el índice de variación en esta operación es:
IV =![]() =1,12
=1,12
Como 1,12=1+0,12 Þ que se ha aplicado un 12% de IVA
21. Solución.
Se mezclan en total: 20 +13 = 33 litros
20.2,2 +13.1,3 = 44 + 16,9 = 60,9 es lo q se paga por los 33 litros.
El litro de la mezcla sale a 60,9:33 =1,85 euros
23. Solución.
Consideramos el capital dividido en 2 +3 +5=10: partes.De las cuales dos partes le corresponderían al primero,. tres partes al segundo y cinco partes al tercero.
Al primero le tocan los 2/10 de 6000 euros.
Al segundo, los 3/10 de 6000 euro.s
Al tercero, los 5/10 de 6000 euros.
Luego les tocará 1200, 1800 y 3000 euros respectivamente
25. Solución
Si en 2 horas llena un grifo el depósito, en una hora llenará 1/2 del depósito
El otro grifo en una hora llenará 1/3 del depósito.
Los dos juntos en una hora llenarán:
1/2 + 1/3 = 5/6 del depósito
Luego para llenar el depósito se necesitaran ![]() =1,2
horas es decir una hora y doce minutos.
=1,2
horas es decir una hora y doce minutos.
28. Solución.
En hacer el trabajo se tardan:
3x8x15=360 horas
Entonces se necesitarán 360:(9x5) =8 días
30. 5
 Por el teorema de Pitágoras:
Por el teorema de Pitágoras:
d2
=52 +52=50Þ d=![]()
Sucesiones numéricas
1. Estudia la regularidad en las siguiente sucesión y la expresión de su término general
·
· ·
· ··· ·····
2. Escribe los cinco primeros términos de las siguientes sucesiones expresadas por su término general:
a) an = 2n-1
b) an = 2n2+1
c) an = 3.2n
d) ![]()
e) ![]()
Solución: a1= 1/2; a2 =2/4; a3 = 3/8; a4 =4/16; a5 =5/32
f) an = n- n2
Una sucesión a1. a2,....an,.... es progresión aritmética si cada término se obtiene del anterior sumándole una cantidad fija a la que llamamos diferencia de la progresión.
De la definición se deduce que si una progresión es aritmética la diferencia entre dos términos consecutivos es constante.
El término general de una progresión aritmética es an =a1+(n-1)d
La suma de los n primeros
términos de una progresión aritmética es: ![]()
Una sucesión a1. a2,....an,.... es progresión geométrica si cada término se obtiene del anterior multiplicándole por una cantidad fija a la que llamamos razón de la progresión.
De la definición se deduce que si una progresión es geométrica el cociente o razón entre dos términos consecutivos es constante.
El término general de una progresión geométrica es an =a1.rn-1
La suma de los n primeros
términos de una progresión geométrica es: ![]()
Si el valor absoluto de r es
menor que 1 se pueden sumar “todos” los términos de la sucesión ![]()
3 Averigua cuáles de las siguientes sucesiones son progresiones. Para ellas averigua el término general
a) 1, 3, 5, 7, 9,.........
Solución: es progresión aritmética de diferencia 2. El término general: an =1+(n-1).2= 2n-1
b) 3, 4, 5, 6, 7, .........
c) 1, 4, 9, 16, 25,.....
d) 2, 5, 10. 17, 26,......
e) 2, 4, 8, 16, 32,........
Solución: es progresión geométrica de razón 2. El término general es an =2.2n-1 =2n
f) –7, -3, 1, 5, 9.....
4. Representa gráficamente las sucesiones a) b) y c) del ejercicio 1.
5. Un banco paga el 5% del dinero que se deposita en él, si no se saca en un año. ¿cuánto te darán al cabo por 12000 euros?
6. ¿En cuanto se transforma 2800 euros al 10 % en un año?¿ y en tres años a interés compuesto?
Solución:
En el primer año se transforma 2800 +2800.0,10= 2800(1+0,10)=
2800.1,10 = 3080 euros
Si al finalizar el primer año no se retira el dinero, en el segundo al capital se le suman los intereses: 3080.1,10=3388 euros
En el tercer año si no se han retirado los intereses se tendrían: 3388.1,10= 3726,8 euros
Nota. Podemos resolver el problema observando que se trata de una progresión geométrica de primer término el capital inicial y de razón el índice de variación.
Es decir:
C F = C I . IV 3 =2800.1,103 = 3726,80 euros
*7. Estudia la regularidad de las siguiente sucesiones y la expresión de su término general.
Nota. Estos números obtenidos sobre figuras poligonales se llaman números poligonales:
Tipo |
orden |
|||||
|
1 |
2 |
3 |
4 |
5 |
.. n |
|
|
TRIANGULARES |
|
|
|
|
|
|
|
a n |
1 |
3 |
6 |
10 |
15 |
a n = |
|
CUADRADOS |
|
|
|
|
|
|
|
a n |
1 |
4 |
9 |
16 |
25 |
|
|
PENTAGONALES |
|
|
|
|
|
|
|
a n |
1 |
5 |
12 |
22 |
35 |
|
|
HEXAGONALES |
|
|
|
|
|
|
|
a n |
1 |
6 |
15 |
28 |
45 |
|
Cuaderno de actividades tercero Matemáticas en la Secundaria