EN ESTA PÁGINA IREMOS COLGANDO EJERCICIOS RESUELTOS DE  EXÁMENES (CURSO 2004-2005)

 

EXAMENES DE ÁLGEBRA (Recuperación)

 

1. Disponemos de 21000 euros para invertir en bolsa. Nos recomiendan dos tipos de acciones. Las del tipo A, que rinden el 7% y las del tipo B, que rinden el 9%. Decidimos invertir un máximo de 13000 euros en las del tipo A y como mínimo 6000 en las del tipo B. Además queremos que la inversión en las del tipo B sea menor que el doble de la inversión en A. ¿Cuál tiene que ser la distribución de la inversión para obtener el máximo interés anual?

Solución

Hay que optimizar la función objetivo: Z = 0,07x+0,09y, sujeta a las siguientes restricciones:

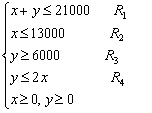
Representamos la región factible:

 

Rectas auxiliares:

r₁  x +y= 21000

x	y
0	21000
21000	0

r₂  x =13.000 (vertical)

r₃ y =6.000 (horizontal)

r₄   y =2x

X	Y
0	0
3000	6000

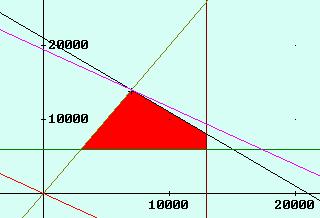
Los vértices son, (3.000,6000), (7.000,14.000), (13.000,8000), (13.000, 6.000)

Gráficamente obtenemos la solución óptima en el punto (7.000, 14.000)

Y el máximo beneficio será 1750 euros.

Comprobarlo analíticamente.

 

1. Bis. Disponemos de 35000 euros para invertir en bolsa. Nos recomiendan dos tipos de acciones. Las del tipo A, que rinden el 8% y las del tipo B, que rinden el 7%. Decidimos invertir un máximo de 22000 euros en las del tipo A y como mínimo 10000 en las del tipo B. Además queremos que la inversión en las del tipo A sea a lo sumo el doble que la inversión en B. ¿Cuál tiene que ser la distribución de la inversión para obtener el máximo interés anual?

Solución

En este caso la función objetivo:

Z = 0,08x+0,07y

Las restricciones:

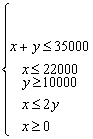
Al igual que en el anterior dibujamos la región factible que es:

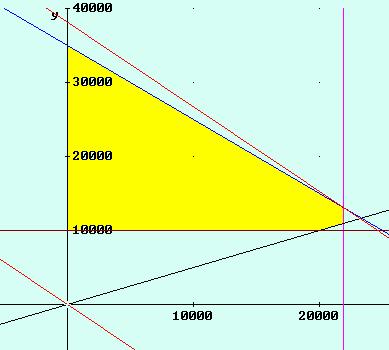
Los vértices son:

(0, 10000), (0, 35000), (22000, 13000), (22000, 11000) y (20000, 10000) y el método gráfico nos da como solución óptima el punto (22000, 13000)

Es decir hay que invertir 22000 en las de tipo a y 13000 en las de tipo B para obtener el máximo beneficio, 2670 euros.

Comprobarlo analíticamente.

 

2. a) Calcula la inversa de la matriz A =,    comprueba el resultado.

b) Resuelve la ecuación matricial  XA – C = 2 B, donde:

A =,    B =  ,    C =

Solución

Primero calculamos el determinante de A para comprobar que en efecto existe la inversa.      

=-1, es distinto de 0, luego hay inversa.

Después calculamos la matriz adjunta de A, cuyos elementos son los adjuntos de los elementos de A

A₁₁=; A₁₂=(-1)¹⁺²..............., es decir

Adj A= 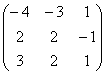, después trasponemos la matriz adjunta

(Adj, A)^t= 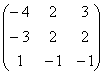, y por último dividimos por el determinante. Nos queda:

A^-1= =

 

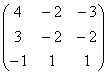
Para comprobar el resultado, multiplicamos por la matriz A (en ambos sentidos) y nos tiene que dar la identidad:

A^-1.A=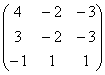.= 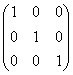(Comprobarlo en el otro sentido)

b) Se tiene:

XA =2B+ C, como la matriz A tiene inversa (apartado a)), multiplicamos a ambos lados para despejar la X:

XA .A^-1= (2B+ C). A^-1, de donde:

X = (2B+ C).A^-1

Calculamos pues, 2B+ C: 

 (2B+ C)= 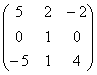, multiplicando por la inversa de A:

X = .=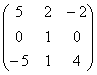

 

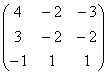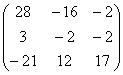
3. En una reunión hay 40 personas. La suma del número de hombres y mujeres triplica el número de niños. El número de mujeres excede en 6 a la suma del número de hombres más el número de niños. Averiguar razonadamente cuántos hombres, mujeres y niños hay.

Solución

Llamamos:

x  al nº de hombres

y al nº de mujeres

z al nº de niños

Se tiene:

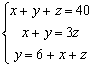
Restando las dos primera ecuaciones, se obtiene 4z=40, de donde z =10.

Sustituyendo:

   Sumando 2y=46,         y =23,            x =7

 

Hacerle usando el método de Gauss

 

CONTINUARÁ

 

 

Si necesitas ejercicios para practicar visita:

 

EJERCICIOS MODELOS

 

Si tienes dudas pregúntalas en el foro: MATEMÁTICAS EN EL SIGLO XXI