Funciones y sus gráficas

Concepto intuitivo de función.

Propiedades de las funciones y su interpretación gráfica: Dominio, recorrido, continuidad, monotonía, extremos relativos.

1. Un médico dispone de 1hora diaria para consulta. El tiempo que podría, por término medio, dedicar a cada enfermo, depende del número de ellos que se acudan:

1 enfermo 60 minutos

2 enfermos 30 minutos

3 enfermos 20 minutos

..... ....... ......... ......

Así hasta un máximo de 30 enfermos. Si llamamos x al número de enfermos e y al de minutos dedicados a cada enfermo escribe la expresión funcional que existe entre ellas ¿ Cómo es la variable independiente, continua o discreta? Dibuja la gráfica ¿ Tiene sentido unir los puntos de la gráfica con una línea?

2. En unos aparcamientos públicos figura la siguiente tarifa de precios:

Tarifa

1ª hora o fracción 1 €

Cada hora más o fracción 0,8 €

Máximo 12 € por 24 horas

Haz una gráfica representativa de la función : tiempo de aparcamiento ....... coste

3. Si un coche va a 80km por hora, ¿ que espacio habrá recorrido al cabo de 2, 3, y 3,5 horas?

a) Dibuja la gráfica de la función espacio-tiempo.

b) ¿Qué tiempo empleará en recorrer 200 y 320km?

Solución

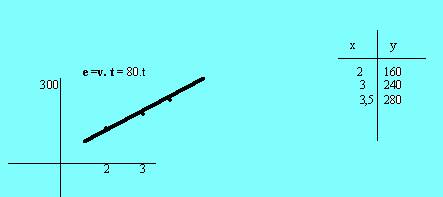
b) Despejando el tiempo tendremos t =e/v:

t = 200/80 = 5/2 = 2horas y media y t = 320/80 =4 horas

4. Representa los siguientes pares (x, y) . Indica la relación entre las variables x e y:

x	1	3	4	5,5	7	....
y	0,75	2,25	3	4,125	5,525	....

5. Dada la tabla

x	0	1	2	3	4	....
y	1	3	5	7	9	....

Representa estos puntos en un sistema de ejes coordenados y escribe la ecuación de la función que relaciona las variables x e y.

6. Halla el dominio de las siguientes funciones:

a) y = 3x b) y = x²-3

c) D =[2, ) d) y = 1/x D = R -{0}

e) f)

g)

Solución. Tiene que ser

Para que un cociente sea positivo numerador y denominador deben tener el mismo signo, es decir:

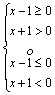ÞÞ D =]È[1,

h)

7. Consideremos f(x) = y g(x) = x², calcula el dominio de la composición. Calcula fog.

8. Calcula la inversa de a) y = 3x -3; b)

8. Estudia la continuidad[1] de las siguientes funciones:

a)

Discontinua en x =0,

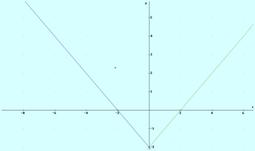
b)

Continua en todos los puntos.

c)

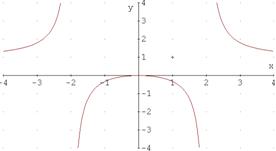
d) 9[2]. Para las funciones del ejercicio anterior, estudia la monotonía, simetría y los máximos y mínimos.

Solución de b) creciente en ]-4, -2[ È]-2, 0[ y decreciente en ]0, 2[È]2, 4 [

simétrica respecto el eje OY

máximo no tiene, el mínimo se alcanza en el 0 y vale 0

Interpolación lineal[3]

En numerosos fenómenos de la naturaleza observamos una cierta regularidad en la forma de producirse, esto nos permite sacar conclusiones de la marcha de un fenómeno en situaciones que no hemos medido directamente.

La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos.

La extrapolación consiste en hallar un dato fuera del intervalo conocido, pero debe tenerse en cuenta que esté próximo a uno de sus extremos, pues en otro caso no es muy fiable el resultado obtenido.

Cuando las variaciones de la y son proporcionales (o casi proporcionales) a los de la variable independiente x se puede admitir que dicha función es lineal y usar para estimar los valores por interpolación lineal..

Sean dos puntos (x_o, y_o), (x_1, y₁), la interpolación lineal consiste en hallar una estimación del valor y, para un valor x tal que x₀< x < x₁. Teniendo en cuenta que la ecuación de la recta que pasa por esos dos puntos es:

obtenemos la fórmula de la interpolación lineal.

Ejercicios

1. Dada la siguiente tabla, obtener por interpolación lineal el valor de .

x	0	1	2
	1	1,4142	1,7321

2. El aumento de líneas telefónicas instaladas en España durante los tres últimos años fue:

Años	2000	2001	2002
Millones de líneas	8,457	8,882	9,640

¿Es lineal el aumento producido?

3. Un investigador ha observado que la vida media de una bacteria varía con la temperatura media en la siguiente forma

Temperatura	6º	9º	12º	15º	16º
Vida media	104,2	140,4	181,7	220,2	257,6

Se pide:

a) Efectuar una representación gráfica, tomando en abscisas las temperatura s y en ordenadas la vida media.

b) Calcular las variaciones de la función “vida media” al variar la temperatura.

c) ¿Los resultados anteriores indican que la vida media varía linealmente con la temperatura?

d) En caso afirmativo, mediante interpolación lineal, obtener la vida media para las siguientes temperaturas: 8º, 10,2º, 14,5º y 15,3º

4. Por un recibo de gas en el que se han consumido 10 m³ se han pagado 50 € y por 16 m³ se han pagado71 €. ¿Cuánto habrá que pagar por un consumo de 15 m³?.

Solución

Puntos (10, 50) y (16, 71), la fórmula de interpolación lineal queda:

_{= €}

5.El número de turistas entrados en España en el período 1985-2000 siguió la siguiente tendencia:

Año	1985	1990	1995	2000
Millones de turistas	26,1	32,1	39,0	44,2

a) Expresar la función definida a trozos que daría, por interpolación lineal, el número de turistas en cada año intermedio.

b) Hallar la previsión para el año 1998 (suponiendo fuese lineal).

c) Calcular el número de turistas en 2004.

Estudio y representación de funciones elementales

1. Halla la pendiente de las rectas que pasan por los puntos:

a) (2. 3) y (-1, 0)

b) (3, 1) y (4, -5) . Solución

2. Halla la pendiente de las rectas:

a) y = -3x +1; b) y = 2-x; c) 3x-2y-4=0; ; d)

3. Representa las siguientes funciones lineales o afines:

a) y =2x ; b) y =3; c) y = 3x-2; d); e)

4.. Halla gráficamente la pendiente de la recta que pasa por los puntos A(-3, -6) y B((3, -2) y escribe su ecuación.

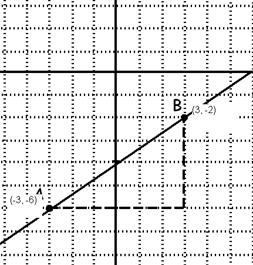Solución

La pendiente según se ve en la gráfica es

la ordenada en el origen es -4

y por tanto la ecuación es

5. Dibuja y halla la ecuación de la recta que pasa por los puntos:

a) (2. 3) y (-1, 0); b) (3, 1) y (4, -5)

6. Hallar la ecuación de cada una de las siguientes rectas:

a) Pasa por el punto (0, 1) y tiene por pendiente 3

b) Pasa por el punto (0, 4) y tiene por pendiente 3/4

c) Pasa por el punto (-3, 3) y tiene por pendiente -4

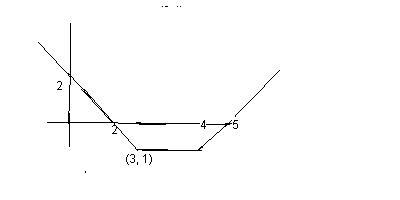
7. Calcula la expresión de la función cuya gráfica se adjunta:

Solución

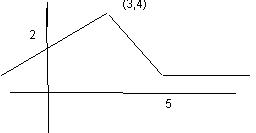Es una función definida a trozos.

El primer trozo pertenece a la recta que pasa por los

Puntos (0,2) y (3,4), Su ecuación es

y = 2x +2

El otro trozo pertenece a la recta que pasa por (3, 4) y (5, 1).

La pendiente es:

y =

El último trozo pertenece a la recta constante y =1

La función es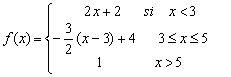

8. Calcula la expresión algebraica de la función cuya gráfica es:

9. Representa en los mismos ejes coordenados las siguientes rectas:

a) y = x e y = 2 – x

Solución

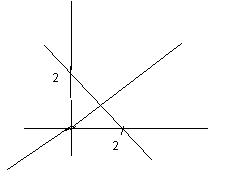
Las rectas se cortan en el punto (1, 1)

b) y = x-3 e y = -x +2; c) e

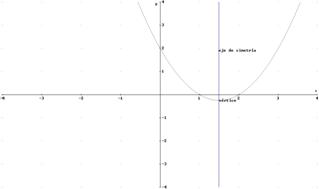
10. Representa la gráfica de la función cuadrática y =x² -3x+2

Solución

Es una parábola. Necesitamos calcular el vértice y los puntos de corte con los ejes

Vértice. La abscisa del vértice está en el punto , en nuestro caso:

;

Los puntos de corte con los ejes:

punto (0,2) x =1, x =2 puntos (1, 0) y (2, 0)

Con estos puntos podemos dibujar la gráfica pues tenemos entre ellos dos puntos simétricos:

11. Representa las siguientes parábolas indicando el vértice y los puntos de corte con los ejes.

a) y =x² ; b); c) y = -3x² +6; d) y = x² +x +1; e) y = x² -5x+6; f) y =-x² +3x-2

12. Dibuja en unos mismos ejes cartesianos la recta y = x- 3 y la parábola y = x² -5x+6.

13. Resuelve gráficamente los siguientes sistemas:

a)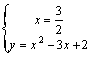

Se dibujan sobre los mismos ejes

(ver ejercicio 22)

Solución V (3/2, -1/4)

b) c)

14. Resuelve analítica y gráficamente el sistema:

15. Representa las siguientes funciones usando una tabla de valores adecuada:

a) ; b) ;

Solución

b).figura 1

x	-1	0	1	3	...
y	1	2	2,4142	3	...

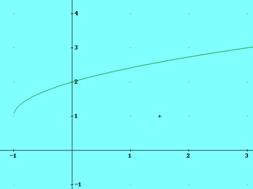figura 1

c) ; d) ; e)

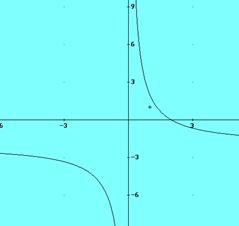
16. Representa las siguientes funciones de proporcionalidad inversa:

a) ; ; b) ; c) ;

d) figura 2

17. Representa las siguientes funciones exponenciales utilizando una tabla de valores:

a) y = 3^x ; b) y = 2^{- x} ;

c) y = (1/2)^-x

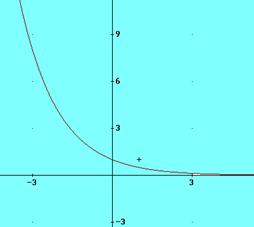figura 3

d) y = 2^x -3

18. La gráfica de una función exponencial del tipo y = k .a ^x pasa por los puntos (0, 4) y (1, 8)´

a) Calcula k y a

b) Representa la función.

19. Representa las funciones: a) y = ln x; b) y = ln (x +1); c) y = log2 x; d) y = log₂ (2-x)

20. Representa las funciones a) f(x)= cos (x + ; b) f(x) = 1+ sen x; c) f(x) = - sen x

21. Dibuja en el intervalo [0, 6] la función que a cada número positivo le hace corresponder su parte entera.

22. Representa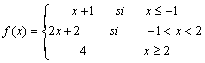

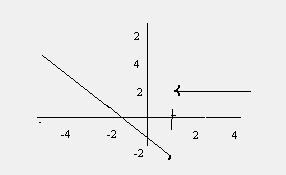
23. Busca la expresión analítica de la siguiente función:

Problemas

1. Antonio ha comprado un coche que le ha costado 19500 €. El coche se deprecia un 20% cada año. Al cabo de un tiempo decide venderlo y le dan 5200 € . ¿Cuántos años han pasado?

Indicación: Haz la gráfica de la situación planteada y encuentra el punto de la gráfica cuya ordenada valga 5200.

2. El consumo de gasolina de gasolina de cierto automóvil, por cada 100km, depende de la velocidad a la que va . a 60Km/h consume 5,7 l y a 90km/h consume 7,2km/h. Estima cúanto consumirá si recorre 100km a 70km/h.

3. El coste de producción de x unidades diarias de un determinado artículo es:

y el precio de venta de uno de ellos es (50-x/4) €

Halla el número de unidades que debe venderse diariamente para que el beneficio sea máximo.

Solución

La expresión de la función beneficio es:

B(x)=(50-x/4)x –((1/4)x² + 35x + 25) = , función cuadrática.

La solución gráfica se ve en la figura, es el vértice de la parábola.

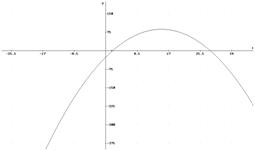
x = 15 unidades.

Nota. Después del tema de derivadas se resolverá de otra forma

4. Un viajero llega tarde a la estación y el tren ya ha salido.

Si las ecuaciones de las trayectorias del viajero y del tren son:

Tren: Viajero

indica si el viajero alcanza el tren y en este último caso el momento del encuentro.

5. Un capital de 12000 € está colocado al 3% fijo anual. Calcula la expresión que nos da el capital acumulado al cabo de t años.

Solución

Se trata de una función de crecimiento exponencial.

El capital en el primer año se convertirá 12000+12000.0,03= 12000(1+0,03)=12000.1,03= C₁,

El capital al cabo de 2 años se convertirá C₁ + C₁.0,03 = C₁(1,03) =12000. (0,03)² ...

y al cabo de t años C(t)=12000.(1,03)^t t0

6. Una sustancia radiactiva tiene un periodo de semidesintegración de 15 años. Tenemos 10 gramos de esa sustancia. Encontrar la función que nos da la cantidad de sustancia radiactiva en función del tiempo transcurrido

7. Un virus se reproduce por división transversal: en 2 horas cada virus se divide en tres. En el día 0 se ha contado un millón de virus de ese tipo y se estudia la evolución de esta población en función del tiempo.

a) Encontrar la expresión de la población en función del tiempo, en horas.

b) ¿Cuál es el efectivo de la población en la primera hora?

c) ¿Cuánto tiempo tardará en doblarse? ¿Y en multiplicarse por 10?

8. El precio del metro cuadrado de baldosas para suelos depende de la cantidad que compremos, x, y viene dado por la función:

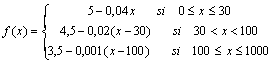
a) Representa gráficamente la función

b) ¿Cuál será el precio si compró 250 m²?

c) Para conseguir un precio inferior a 3 € /m² ¿cuántos m², como mínimo, tengo que comprar?

Límites

Estudia si tienen límite las siguientes funciones, en los puntos indican:

1. en x =0 y x =1

Solución

En x =0 la función tiene límite y vale -2

En x =1 no existe el límite, pues los límites laterales no coinciden.

2. en x =2

3. ; 4.

5. En x =0 y cuando x tiende a +

6. x.

Solución: x =

7. 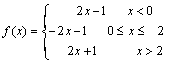; en x =0 y x =2

8. En x =0 y x =1

Calcula las asíntotas de las siguientes funciones y sitúa la curva con respecto a ellas:

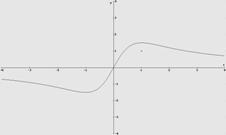1.

Solución.

Verticales no tiene pues el dominio es todo R

Horizontales

, y =0 , no hay oblicuas

2. ; 3. ; 4. y =e^-x ; 5. y =ln (x²-1)

Calcula los siguientes límites, caso de que existan:

1.

Solución: Es una indeterminación del tipo . Por tanto se simplifica la fracción y se vuelve a calcular el límite:

=

2.

3.

4.

5.

Solución es una indeterminación del tipo

=

=

6.

7.

8.

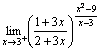
9.

Solución.

Es una indeterminación del tipo

=

10.

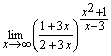
11.

12.

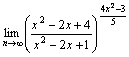
13.

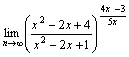
Solución

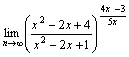= 1^4/5=1

14.

15. ==0

16. ; 17*.

Continuidad

1. Estudia la continuidad de las siguientes funciones:

a)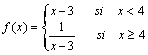

b)

2.Dada la función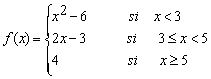

Estudia los puntos en que f es discontinua y clasifica las discontinuidades que presenten. Representación gráfica.

3. Dada la función:

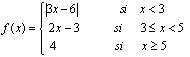
Estudia los puntos en que f es discontinua y clasifica las discontinuidades que presenten.

4. Calcula el valor de k para que las siguientes funciones sean continuas:

a)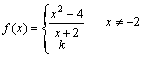

b)

Actividades propuestas

1. A qué clase de números reales pertenecen: 3/4; -2; ; 1,3333...; 3P;

2. Ordena de mayor a menor los siguientes números: -2/5,, 10/9, -3, 1/33333

3. Representa sobre la recta los siguientes conjuntos:

a) ; b) ; c)

4. Escribe en forma de intervalo los siguientes conjuntos:

a) ; b) 2x > -3; c) -1 £ x + 2 £ 0; d)

5. Resuelve la ecuación .

6. Calcula el dominio de:

a) ; b) f(x) = ; c) .

7. Estudiar la simetría de las funciones siguientes:

a) f(x) = - 3x² + 1; b) f(x) = x³ - 3x; c) .

8. Estudiar si están o no acotadas las siguientes funciones:

a) f(x) = x² - 5 ; b) ; c) f(x) = .

9. Analiza la función cuya gráfica es la siguiente:

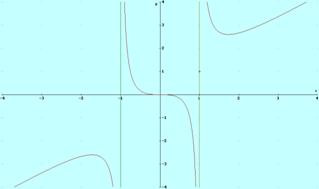
10. Calcula la inversa de . Comprueba el resultado

11. Dada la función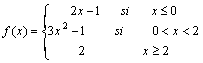

a) Representación gráfica.

b) Clasifica los puntos de discontinuidad.

12. Representa una función que verifique las siguientes condiciones:

, , y

13. En una empresa se hacen montajes en cadena. El número de montajes realizados por un aprendiz depende de los días de aprendizaje, según la función , t en días.

Representa la función sabiendo que el periodo de aprendizaje es de 30 días. ¿Cuántos montajes realiza el primer día?¿y el 30?

¿Qué ocurriría con el número de montajes si nunca se acabara el aprendizaje?

Tasa de variación media. Interpretación geométrica de la derivada

Si necesitas Teoría de derivadas visita la siguiente página: Derivadas

1. Halla la tasa de variación media de la función

f(x) =3-x² en el intervalo [0,2]

Solución

T.V.M. [0, 2] =

2. Halla la tasa de variación media de la función f(x)= x²-3x-2 en los intervalos [0, 1] y [0, 2]

3. Calcular b para que la tasa de variación media de la función f(x) = ln (x +b) en el intervalo [0,2] valga ln2.

4. Calcula la derivada en x =0

Luego la función valor absoluto no es derivable en el 0.

5. Calcula la derivada de la función f(x)=x²-4 en x =0 y x =1

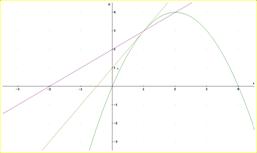Ejemplo.

En la figura se muestra la gráfica de y =-x² +4x, una recta secante que pasa por el punto (1, 3) y la recta tangente en ese punto, que tiene por ecuación

y –3 = 2(x-1)

6. Hallar la ecuación de la recta tangente a la gráfica de f(x) = x²-x +5 en x =1

Solución

f(1) = 5

f' (x)= 2x-1 , f’(1)=1

la ecuación será y – 5 = (x-1) , ó y =x +4

Hacerlo usando la definición de derivada

7. Calcula la ecuación de la recta tangente a la curva y = 2x³ - 5x en el punto de abscisa x₀ = 1

8. Sea , se pide: a) derivada de f ;

b) ecuación de la recta tangente en el punto de abscisa x = 0.

Cálculo de derivadas

Calcula la derivada de las siguientes funciones

1. y =2x⁴ -3x²+ 2x-1; 2. y = (2x+1)(3x³-1); 3. ; 4. f(x)= ; 5. ; 6. ; 7. y = e^3x+5; 8. y = sen(3x + 5); 9. ; 10. y = e^3x+5 sen(3x + 5)

Aplicaciones de las derivadas

CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS

Si necesitas Teoría de derivadas visita la siguiente página: Derivadas

1. Estudias la monotonía y calcula los extremos de las siguientes funciones (en caso de que existan):

a). f(x)=-x³ +3x (representa la función)

b) (representa la función) ;

c)

d)

e) ; f)

2. El coste de producción de x unidades diarias de un determinado artículo es:

y el precio de venta de uno de ellos es (50-x/4) €

Halla el número de unidades que debe venderse diariamente para que el beneficio sea máximo.

Si necesitas Teoría de derivadas visita la siguiente página: Derivadas

Si necesitas mas ejercicios y problemas de derivadas (resueltos) y sus aplicaciones visita Matemáticas en el Bachillerato

---

[1] Se formalizará después de los límites

[2] De forma intuitiva, se formaliza después de las derivadas.

[3] Se incluye resumen teórico