ECUACIÓN DE LA RECTA TANGENTE A LA GRÁFICA DE UNA FUNCIÓN DERIVABLE

 

1. a) Usando la definición, calcula la derivada de f(x)=  en x =2.

 

 b) Hallar la ecuación de la recta tangente a la gráfica de f(x)=  en el punto de abscisa x =2,

Solución

a) Se verifica f(2)= 0  y por lo tanto:

 f’(2)==

 

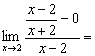
(Se ha simplificado el factor x-2 que estaba en el numerador y el denominador)

 

b) La ecuación de la recta tangente a la gráfica de f en el punto (a, f(a)) tiene la expresión:

y- f(a)=f’(a)(x-a)

(Ya que la derivada en el punto de abscisa x = a, es la pendiente de la recta tangente en el punto (a, f(a))

En este caso f(a)=f(2)=0 y f’(2)=1/4

Con lo q sustituyendo en este caso te queda:

Y -0 = (1/4)(x-2) (ecuación punto pendiente de la recta tangente a la gráfica de f en el punto  (2, 0)),

Despejando  y = (1/4)x -2 (su ecuación explícita)

2. ¿Qué valor debe tener a para que la recta y =-x +6 y la curva y =-ax² +5x –1 sean paralelas en x = 1.

Solución

Para que la curva sea “paralela” a la recta, la pendiente de la recta tangente en ese punto debe ser igual a la pendiente de la recta, por lo tanto:

-1=-2a.1+5, de donde,   2a=6 y a =3

 

3. Determinar m para que la tangente a la curva y = -x²-(2m+1)x + m + 2, en x =2, sea paralela a la recta 3x-y +2=0

Solución

Para q sean “paralelas” la tangente a la curva y = -x²-(2m+1)x + m + 2, en el punto de abscisa 2,  tiene q tener la misma pendiente que la recta  3x-y +2=0,  que en este caso vale 3.

Como la pendiente es la derivada (en x =2), se tiene:

y' = -2x –(2m+1),   y’(2)= -4-2m-1=3 de donde        2m=-8         y despejando  m =-4

 

4. Sea la función f(x)= x²+ ax +3, xR. Determinar el valor de a para que la grafica de f tenga una tangente en el punto de abscisa x=1, que sea paralela a la recta 2x+y= 0

Solución

(Ver el problema anterior)

Si queremos que sea paralela a la recta 2x+y=0, la tangente a la gráfica de f tendrá que tener su misma pendiente.

La pendiente de la recta 2x+y= 0 es -2,  como la pendiente de la recta tangente a la gráfica es la derivada, por tanto la derivada en x=1 de la función f(x)= x²+ ax +3 debe valer  -2.

f’(x)=2x+a    y en el punto de abscisa 1,         f’(1)=2+a      2+a=-2,        de donde  a=-4

 

continuará