PRUEBAS DE ACCESO A FACULTADES, ESCUELAS TÉCNICAS Y COLEGIOS UNIVERSITARIOS

 

CONVOCATORIA DE JUNIO 2004

MODALIDAD DE BACHILLERATO: DE CIENCIAS DE LA NATURALEZA Y DE LA SALUD Y DE TECNOLOGÍA

EJERCICIO A

PROBLEMA 1. Dado el sistema de ecuaciones lineales 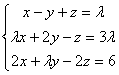, con parámetro real, se pide:

a) Determinar razonadamente para que valores de es compatible determinado, compatible indeterminado e incompatible.

b) Hallar el conjunto de las soluciones del sistema para el caso compatible determinado.

c) Hallar el conjunto de las soluciones del sistema para el caso compatible indeterminado.

PROBLEMA 2. Dados los planos  y la recta , se pide:

a) Determinar razonadamente la posición relativa de la recta r y la recta s intersección de los planos  y

b) Obtener razonadamente la ecuación del plano que contiene a la recta s anterior y es paralelo a r.

PROBLEMA 3. Encontrar razonadamente el punto de la curva en el que la recta tangente a la curva tiene pendiente máxima y calcular el valor de esta pendiente

PROBLEMA 4. 1. En un plano, el trazado de una carretera discurre según la ecuación siendo un río el eje OX. En el terreno entre el río y la carretera hay un pinar. Si expresamos las distancias en kilómetros ¿cuánto vale el pinar si la hectárea se paga a 60 €?

PROBLEMA 4. 2. La media de las calificaciones globales obtenidas por 10 alumnos fue 6,8 puntos y sus horas de estudio totales sumaron 120. Si x representa las horas de estudio de cada estudiante e y su calificación obtenida, el coeficiente de correlación entre x e y es 0,8. Sabiendo que la desviación típica de x coincide con la de y, explicar, razonadamente, cómo se obtiene la recta de regresión de y sobre x y calcularla.

CRITERIOS DE CORRECIÓN

PROBLEMA 1. a) Por razonar que el sistema es compatible determinado si es distinto de -2 y 3, que si =-2 es incompatible y si =3 es compatible indeterminado, hasta 1,3 puntos

 b)  (con -2, 3) hasta 1 punto

c) (x, y, z)=(3, 0, 0) +a(-1, 4, 5) , con a real, hasta 1 punto

PROBLEMA 2.  A) Por El planteamiento, hasta 1 punto. Por la respuesta correcta, (se cruzan) hasta 1,7 puntos. B) Por el planteamiento, hasta 1 punto. Por la respuesta correcta, 8x-6y+z+12=0, hasta 1, 6 puntos.

PROBLEMA 3.  Cálculo de la pendiente, hasta 1 punto. Derivada de la pendiente y determinación de los puntos críticos (x =), indicando dónde se alcanza el máximo (en x=-1/), hasta 1,8 puntos. Y por el valor de la pendiente máxima (9/(8)), hasta 0,5 puntos.

PROBLEMA 4. 1. Por el planteamiento correcto, hasta 1,5 puntos. Por calcular el valor del área perdida en kilómetros cuadrados (8/3), hasta 1 punto; si se expresa en hectáreas, hasta 1,2 puntos. Por el valor del pinar (16000 € ), hasta 0,6 puntos.

PROBLEMA 4. 2. Por la explicación de la obtención de la recta de regresión de y sobre x, hasta 2 puntos. Por el cálculo de dicha recta (y-6,8=0,8(x-12)), hasta 1, 3 puntos.