En esta página se pretende recoger algunos modelos de problemas propuestos en las OLIMPIADAS MATEMÁTICAS INTERNACIONALES, así como sus soluciones.

Se irá actualizando periódicamente y los ejercicios se propondrán unos días antes en el foro.

Espero que disfrutéis con ellos.

 

BREVE RESEÑA HISTÓRICA

La expresión “Olimpiada Matemática” se utiliza por primera vez en 1934 en Leningrado. y  se usa de nuevo en la olimpiada local de Moscú al año siguiente.

Pero fue en 1959 cuando la  sociedad rumana de Matemáticas y Físicas invita formalmente a participar en una competición común a varios países del este, utilizando el nombre de Primera Olimpiada Matemática Internacional. Se celebró en Bucarest.

En 1967 participaron por primera vez países occidentales invitados por Yugoslavia, Inglaterra, Francia, Italia y Suecia.

En 1974 entra en la competición Estados Unidos,  invitado por la República Democrática Alemana.

España participa desde 1982 invitada por Hungría.

 

Hoy día se utiliza esta expresión, Olimpiada Matemática, en muchas competiciones nacionales destinadas a estudiantes de Enseñanza Secundaria.

 

PROBLEMAS PROPUESTOS EN LAS O. M. I

 

1. Sean p y q dos números naturales tales que:

 

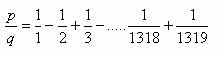
Propuesto por  la República federal Alemana en las Olimpiadas Matemáticas celebradas en Londres, en 1979.

 

Solución

Transformemos de la siguiente forma:

=

=

 

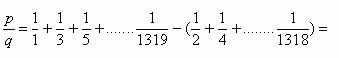
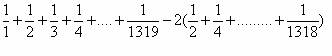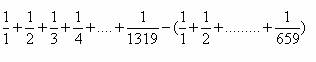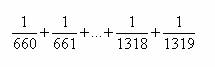
Agrupamos estas fracciones en pares (la 1ª con la última, la segunda con la penúltima...):

 

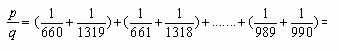
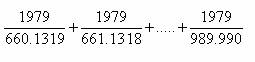
Como 1979 es  primo ningún denominador es divisible por 1979. además q es el mínimo común múltiplo de los denominadores y entonces q y 1979 son primos entre sí. Por tanto:

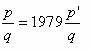  de donde   p = 1979.p’, es decir es divisible por 1979 (c.q.d)

 

2. Se cortan dos círculos en el plano. Sea A uno de los puntos de la intersección. Dos puntos, que parten simultáneamente de A, se mueven con velocidades constantes y con el mismo sentido, cada uno sobre su propia circunferencia. Ambos puntos regresan al punto A simultáneamente después de una vuelta. Probar que existe un punto P del plano tal que, en cualquier instante las distancias desde P a los puntos que se mueven son iguales.

 

Solución

Consideremos la siguiente figura:

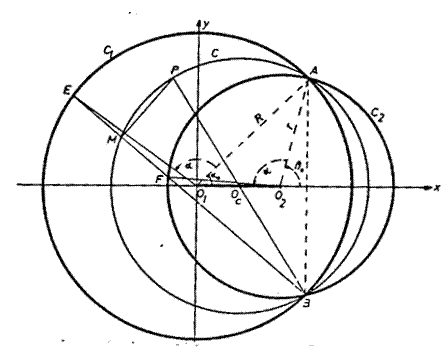
En cada instante los puntos móviles E y F sobre las circunferencias (c₁) y (c₂), respectivamente determinan un segmento ,  cuyo punto medio designamos con M. Al variar E y F en el transcurso del tiempo, el punto M recorre una circunferencia pasando por A y B:

En efecto, consideremos un sistema cartesiano rectangular cuyo eje de abscisas sea la recta que une los centros de las circunferencias (c₁) y (c₂) y cuyo eje de ordenadas, su perpendicular por O₁ (ver figura) , las coordenadas de los puntos A, B, E y F son:

 

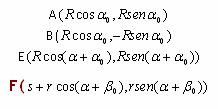
en que s denota la longitud del segmento que une los centros de las circunferencias (c₁) y (c₂) y  el ángulo descrito por los puntos E y F en su movimiento uniforme por sendas circunferencias. El punto M tendrá de coordenadas:

M:

De aquí se obtiene la trayectoria descrita por M:

, que es una circunferencia de centro y cuyo cuadrado del radio resulta:

 

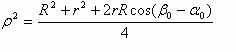
Además la circunferencia (c) pasa por A (y  por tanto por B) al que corresponde :

M: x =

        

y =

 

Por otra parte, el punto F está en todo momento en la recta BE, pues los ángulos ABE y ABF que están inscritos en los círculos delimitados por (c₁) y (c₂), respectivamente, tienen como se observa en la figura, la misma medida . Así pues, los puntos E, F y B son colineales en todo instante.

Finalmente, las mediatrices de los segmentos originados por los puntos móviles E y F, formarán con las rectas correspondientes EB, ángulos inscritos en la circunferencia (c) de vértices los puntos M, por ser rectos, tales mediatrices pasarán por el punto P de (c ). Que es el extremo del diámetro trazado por B. Por tanto, en todo instante, las distancias  y  son iguales. (c. q. d)

 

continuará