Como muestra incluyo aquí un artículo que publicó hace mas de 20 años, pero que sigue siendo actual.
Si te interesa te recomiendo que visites 
“Algunos aspectos insólitos de la actividad matemática”
Miguel de Guzmán (1936-2004)
Indice
Filosofía y
matemáticas
Matematización del
pensamiento
Matemática como modelo del
pensamiento
Matemática y estética
La belleza matemática
Creatividad matemática
Matemática como instrumento
de exploración
Aplicabilidad de la
matemática
La matemática como juego
La matemática, aventura del
pensamiento
Filosofía y matemática
En muchas de las etapas más importantes de la filosofía, el pensamiento matemático ha sido considerado como modelo de conocimiento. La tendencia es bien patente en los pitagóricos, para quienes la misma constitución ontológica del universo es número y armonía. Así se expresa solemnemente Filolao en el siglo V a. C.: "Grande, todopoderosa, todoperfeccionadora y divina es la fuerza del número, comienzo y regidor de la vida divina y humana, participante en todo. Sin el número todo carece de fronteras y es confuso y oscuro. Porque la naturaleza del número proporciona conocimiento y es guía y maestra para todos en todo lo que es dudoso o desconocido. Porque nada de las cosas nos sería claro ni en su mismo ser ni en sus relaciones mutuas si no existiera el número y su esencia. Este es quien armoniza en el alma las cosas con su percepción, haciéndolas cognoscibles y congruentes unas con otras según su naturaleza, proporcionándoles corporeidad" (Diels, B. 1 l).
Tras las fórmulas concisas que nos han llegado de los pitagóricos que, interpretadas al pie de la letra, pueden resultar un tanto estrafalarias, urge explicitar ese respeto y veneración por la forma y cuantificación, extraordinariamente modernos, que siguen siendo valederos para la ciencia actual. Esta actitud pitagórica ha perdurado a lo largo de la historia del pensamiento con notable firmeza. Platón es el intérprete, al mismo tiempo transmisor y purificador, del pensamiento pitagórico. Cuando el alma se queda a solas (aute kaz' auten) ante el mundo inteligible (kosmos noetos) y trata de conocer el ser de las cosas, debe descomponer cada una de las ideas en sus elementos. Así llega a los elementos más simples (atomon eidos) . Clasificada de esta manera, la idea compleja tiene una determinada clave numérica. Esta es la traducción platónica de la expresión más ontológica de los pitagórícos. El pitagorismo renace en el neopitagorismo del siglo I a. C. y en el neoplatonismo de los siglos III al VI p. C. Macrobio, entre los romanos, con su Comentario al sueño de Escipión, es uno de los transmisores de la Edad Media de esta corriente del pensamiento.
 Galileo, a medio camino entre el Medievo y la Edad Moderna, se
expresa así en su vejez: "Opino en verdad que el libro de la filosofía es
el de la naturaleza, el cual se encuentra perpetuamente abierto ante nuestros
ojos, pero como está escrito en caracteres diferentes de los de nuestro
alfabeto no puede ser leído por todos. Los caracteres de este libro son
triángulos, cuadrados, círculos, esferas, conos, pirámides y otras figuras
matemáticas muy propias para una lectura de tal género" (Carta a
Licatti, 1641).
Galileo, a medio camino entre el Medievo y la Edad Moderna, se
expresa así en su vejez: "Opino en verdad que el libro de la filosofía es
el de la naturaleza, el cual se encuentra perpetuamente abierto ante nuestros
ojos, pero como está escrito en caracteres diferentes de los de nuestro
alfabeto no puede ser leído por todos. Los caracteres de este libro son
triángulos, cuadrados, círculos, esferas, conos, pirámides y otras figuras
matemáticas muy propias para una lectura de tal género" (Carta a
Licatti, 1641).
Por su parte Descartes, a fin de avalar las afirmaciones del Discurso sobre el método, escoge una parcela del conocimiento privilegiada en que sus principios puedan aparecer más claramente ejemplificados. Esta es precisamente la geometría, junto con la dióptrica. La matemática, para él, constituye "un modo de habituar el espíritu a nutrirse con verdades y no contentarse con falsas razones".
Matematización del pensamiento
La matematización del pensamiento como camino científico es hoy un dogma, a veces llevado a extremos ridículos, de la ciencia moderna. Kant llega a afirmar que "en cada una de las disciplinas de la naturaleza solamente se puede encontrar tanto de auténtica ciencia cuanto se encuentra en ella de matemática" (Metaphysische Anfangsgründe der Naturwissenschaft. Vorrede). Y la tendencia de todas las parcelas del conocimiento a fin de aumentar su credibilidad y su prestigio ha sido en los últimos tiempos, y sigue siendo, hacia el revestimiento, natural o forzado, de estructuras matemáticas.
Puede uno preguntarse: ¿Merece la matemática este lugar privilegiado que se le ha atribuido de una forma tan constante? No han faltado filósofos que han considerado injustificada y aun nociva esta influencia invasiva del pensamiento matemático. Heidegger, con un juego de palabras, ha tratado de expresar la cuestión: la matemática "ist nicht strenger, sondern nur enger" (no es más exacta, sino sólo más estrecha). Y no sin cierta razón. El conocimiento humano contiene muchas más riquezas que las que el pensamiento matemático puede abarcar. Existen realidades profundas que el hombre, más o menos conscientemente, ansía aprehender cognoscitivamente que escapan a la matemática. Esta llega fundamentalmente a dominar la componente raciocinante del pensamiento sin tocar siquiera otras facetas del conocimiento intelectual. Desde el conocimiento matemático al conocimiento personal, que involucra a todo el hombre, existe ciertamente un abismo. El matemático y filósofo B. Pascal ha expresado así en sus Pensamientos la diferencia entre el espíritu matemático (esprit de géométrie) y el espíritu de discreción (esprit de finesse): "En el primero los principios son obvios pero alejados del uso común, de modo que cuesta girar la cabeza hacia este lado por falta de hábito. Pero por poco que se la vuelva se ven estos principios plenamente y sería necesario tener el espíritu totalmente falseado para razonar mal sobre principios tan toscos que es casi imposible que se escapen. Pero en el espíritu de discreción los principios son de uso común y están ante los ojos de todo el mundo. No hay que girar la cabeza ni hacerse violencia. No hay más que tener buena vista, pero es necesario tenerla buena, pues los principios son tan finos y numerosos que es casi imposible que no se nos escapen. Ahora bien, la omisión de un principio conduce a error. Por tanto es preciso tener la vista bien limpia para verlos todos y además un espíritu bien sano para no razonar falsamente sobre estos principios conocidos".
Y con todo, el pensar matemático merece un lugar privilegiado en
el conocimiento por razón de su adecuación a su propio objeto, su evidencia y
su certeza. No se trata de pensar con Leibniz que haya de venir el día en que
dos filósofos de opiniones encontradas, en lugar de discutir sobre ellas, se
sienten y digan: "Calculemos". Pero sí se puede afirmar que la
matemática es un intento de creación de un universo para la satisfacción del
ansia de conocimiento del hombre, hecho por éste a la medida de su propia mente.
Intento no del todo logrado, pues, como veremos más adelante, este universo no
carece de grietas
inquietantes. Esto lo hace de nuevo más cercano a la frágil condición de
hombre, "esa caña pensante", como lo definió el mismo Pascal. Se diría
que su seguridad le viene a la matemática de su carácter fundamentalmente
tautológico, pero también es verdad que las tautologías que constituyen la rica
estructura matemática representan un triunfo lleno de belleza y útiles
implicaciones sobre el carácter reptante del raciocinio humano.
Matemática como modelo de pensamiento
La perfección del pensamiento matemático ha llevado a considerarlo en muchas etapas de la historia de la humanidad como instrumento de comunión con la divinidad y con las fuerzas ocultas del mundo. Muchos de los monumentos megalíticos y ciclópeos, las pirámides de los egipcios, algunas de las construcciones de ciertas culturas precolombinas, la astrología de la antigüedad y de los tiempos modernos conservan entreverados elementos matemáticos. Los pitagóricos hicieron del cultivo a las matemáticas una secta religiosa con sus ritos y sus secretos. En la Biblia abundan los elementos numéricos con significados ocultos y la Cábala está plagada de ellos. En este aspecto ocupa un lugar importante el Ars magna et ultima de nuestro Ramón Llull (1235-1315), un sistema de conceptos y proposiciones primitivas que, por manipulación mecánica, darían lugar a todas las ciencias particulares, incluida la teología. Con ella se adelantó en varios siglos a la Characteristica universalis de Leibniz, que en su intento se confiesa inspirado por la obra de Llull. Entre los matemáticos más famosos no han faltado quienes han cultivado seriamente estos aspectos cuasimísticos de la matemática. En su Harmonice Mundi (1619), donde Kepler escribe su tercera ley sobre el movimiento de los planetas (el cubo de los ejes es proporcional al cuadrado de los períodos), se describen las relaciones armónicas matemáticas y musicales entre los planetas a través de las cuales Dios se da a conocer al oído espiritual de los hombres. Incluso Newton dedicó una buena parte de su energía a desvelar los misterios de la astrología de su tiempo, una faceta poco conocida de uno de los mayores matemáticos de todos los tiempos.
¿De dónde le viene a la matemática su carácter modélico? Su constitución puramente formal, sistema de postulados y leyes de inferencia con los que se van obteniendo los teoremas, la hace en cierto modo independiente de toda otra realidad que no sea la mente en su calidad raciocinante. De ahí su carácter incontrovertible y universal frente a opiniones, modas y progresos. Decimos "en cierto modo independiente", pues la elección de postulados e incluso de las leyes de inferencia es un acto que depende de la voluntad del matemático y de las convenciones de la comunidad matemática del momento. B. Russell ha dicho, aludiendo al carácter formal de la matemática, que se trata de "una ciencia en la que no sabemos de qué hablamos ni si lo que decimos es verdad o no". Pero esto es una verdad a medias. Lo que así se describe no es la matemática. Es solamente la estructura de su andamiaje lógico. La matemática nació como ciencia y sigue siéndolo y, por tanto, trata en sus desarrollos de desvelar y dominar alguna porción del mundo real, interior o exterior al hombre. Por eso no es un mero arbitrario juego lógico. Sus postulados y sus leyes de inferencia están fuertemente inspirados en una fracción de la realidad. Es de aquí de donde le viene a la matemática su complejidad y su riqueza, reflejos de la riqueza y complejidad del mundo real mismo. El misterio de la adecuación de ese mundo matemático, tan propio de la mente que ha surgido de ella y de una mirada suya al universo, con la realidad externa es algo que no ha dejado de maravillar a los científicos de todos los tiempos. Este aspecto, origen de la aplicabilidad de las matemáticas, será considerado más adelante. También tendremos que considerar las serias limitaciones que en la estructura de la matemática han hecho patente los modernos progresos de la lógica reciente.
Pese a todo ello podemos afirmar que existen razones poderosas para considerar el conocimiento matemático como modelo de conocimiento científico, ya que ningún otro tipo de ciencia alcanza su objetivo propio con tanta eficacia, evidencia y certeza como lo logra el método matemático.
La afirmación de la naturaleza artística de la matemática puede sonar extraña en muchos oídos. Si arte es la producción por parte del hombre de un objeto bello, espero que esta afirmación resulte justificada al término de las notas que siguen. Desde que se empezó a analizar lo que es arte y belleza aparece explícita esta aseveración. Para los pitagóricos, la armonía, uno de los ingredientes de la belleza, va unida al número en la constitución ontológica de todo el universo. Aristóteles mismo se expresa así en su Metafísica (Libro XII cap.III, v. 9): "Las formas que mejor expresan la belleza son el orden, la simetría, la precisión. Y las ciencias matemáticas son las que se ocupan de ellas especialmente".
Son muchos los testimonios que confirman la existencia de un verdadero placer estético en la creación y contemplación matemática. Así se expresa H. Poincaré en La Valeur de la Science: "Más allá de la belleza sensible, coloreada y sonora, debida al centelleo de las apariencias, única que el bárbaro conoce, la ciencia nos revela una belleza superior, una belleza inteligible únicamente accesible, diría Platón, 'a los ojos del alma', debida al orden armonioso de las partes, a la correspondencia de las relaciones entre ellas, a la euritmia de las proporciones, a las formas y a los números. El trabajo del científico que descubre las analogías entre dos organismos, las semejanzas entre dos grupos de fenómenos cualitativamente diferentes, el isomorfismo de dos teorías matemáticas es semejante al del artista".
Tal vez uno de los testimonios más elocuentes de esta afirmación sea el diario personal de Gauss. En este diario, escrito para él mismo especialmente en la etapa anterior a sus veinte años, período de muchos de sus grandes descubrimientos, va anotando, con un laconismo lleno de fuerza y de entusiasmo, sus observaciones sobre el universo matemático que se va desvelando ante sus ojos asombrados.
Pero este mismo placer estético en la contemplación matemática se da, en menor grado naturalmente, en todos aquellos a quienes se les presentan adecuadamente los hechos y métodos más salientes de la matemática elemental. Por supuesto que el goce estético de la matemática se encuentra en el mundo de la armonía intelectual, y así su percepción requiere una preparación inicial tanto mayor cuanto más elevado sea el objeto que se presenta. Por otra parte, así como el placer que puede proporcionar la pintura y la música, dirigidas a nuestros sentidos, al menos de modo inmediato, es perceptible hasta cierto grado con una contemplación más o menos pasiva, el placer estético de la matemática exige sin duda un grado de participación activa mucho más intenso. En el mundo de la matemática, a fin de gozar del objeto bello que se presenta, es necesario crearlo o recrearlo, de tal modo que el goce estético aquí presente es comparable más bien con el de hacer música, cantar, danzar, pintar, fabular...
Analicemos un poco más a fondo el origen de esta belleza matemática colocándonos desde una perspectiva clásica. La belleza en general ha recibido muchas definiciones. S. Alberto Magno definió la belleza en el objeto como splendor formae, el resplandor del núcleo fundamental del ser, su unidad (armonía interna), su verdad (es decir su inteligibilidad y adecuación consigo mismo y con el mundo en su entorno), su bondad (su capacidad de llenar sus tendencias propias y las de los seres a su alrededor). Estas cualidades deben resplandecer de modo que sean accesibles y deleitables sin áspero trabajo. Otra definición clásica de la belleza que atiende a la componente subjetiva es la de Sto. Tomás de Aquino: Pulchra sunt quae visa placent. Bello es aquello que resplandece luminoso en su propio ser de modo que a quien lo mira le proporciona el sosiego y la facilidad de una percepción perfecta: la contemplación estética. Es aquello que se manifiesta de tal forma que produce una actividad armoniosa y compenetrada de las capacidades anímicas del hombre.
No se puede tampoco pretender describir la belleza matemática con un simple trazo. Me limitaré a señalar unos cuantos elementos de belleza que, a mi parecer. constituyen componentes bastante típicas en la actividad matemática. Un tipo de belleza matemática consiste en el orden intelectual que ante hechos aparentemente inconexos comienza a aparecer. Como un paisaje desde lo alto de la montaña que se desvela de una bruma que lo cubría. Todo el objeto contemplado aparece en conexión y la unidad lo invade. Entes aparentemente diversos que surgen en contextos diferentes resultan ser el mismo o estar ligados por una estructura armoniosa. La contemplación fácil de esta unidad inesperada es sin duda una de las fuentes de gozo estético de muchos hechos matemáticos.
Por poner un ejemplo tomado de la geometría elemental, consideremos cómo surgen las cónicas mediante la sección de un cono circular recto por un plano (ver el recuadro 1). La sola contemplación de una figura bien trazada nos muestra enseguida que la elipse que así se define es el lugar de los puntos del plano cuya suma de distancias a dos puntos fijos es una longitud constante y que, al mismo tiempo, esta elipse es también lugar geométrico de todos los puntos tales que la razón de distancias a un punto y a una recta fija es igual a una constante, hecho nada sencillo de probar analíticamente.
Otro tipo de gozo matemático consiste en la realización de una ampliación de perspectivas con la que de una visión parcial se llega a la contemplación total de un objeto mucho más esplendoroso, en el que nuestro cuadro inicial queda englobado ocupando su lugar justo. En la exposición actual de la teoría de los números naturales, enteros, racionales, reales, complejos, se resume toda una aventura apasionante del espíritu humano que, a través de más de sesenta siglos de historia escrita, ha tenido sus callejones aparentemente sin salida, sus idas y venidas, sus paradojas.
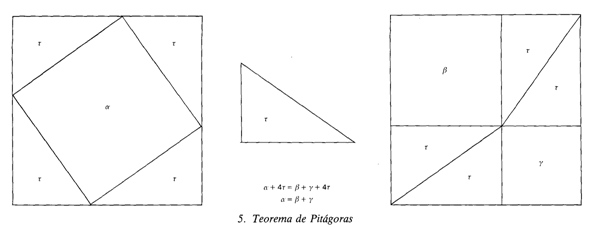
Otro elemento estético presente muchas veces en la creación matemática consiste en la posibilidad de una contemplación descansada e inmediata de una verdad profunda, inesperada y llena de implicaciones. Como ejemplo de la matemática elemental puede citarse la demostración, que no requiere palabras, del teorema de Pitágoras que se presenta en el recuadro 5. o bien la demostración de uno de los resultados favoritos de Arquímedes que se presenta en el recuadro 2.
Para mí mismo, el haberme percatado hace unos años de la posibilidad de llevar a cabo la elegante demostración del teorema de Brianchon, de tanta profundidad e importancia para la geometría proyectiva, que se presenta en el recuadro 3, constituyó un motivo de goce estético enormemente intenso. No es que se pueda afirmar que todo el contenido de la matemática presente el mismo grado de belleza, ni siquiera que contenga belleza. Es indudable que el que una proposición sea cierta no implica que sea bella. Que 2^32 + 1 es el producto de los números primos 641 y 6700417 es una verdad matemática interesante por motivos históricos, pero carente de gran belleza intrínseca. Existen teoremas claramente feos. Muchas teorías, en su nacimiento penoso y reptante, han resultado en un principio confusas y desprovistas de unidad y belleza. El cálculo infinitesimal de los tiempos de Newton y Leibniz constituye probablemente uno de los logros más importantes y útiles de la ciencia moderna, pero el grado de confusión y fealdad en que en un principio se encontraba contribuyó bastante a que su expansión y aceptación fuesen mucho más lentas de lo que la teoría merecía.
¿Qué características debe ofrecer un hecho matemático para que se pueda calificar como bello? La belleza matemática parece incluir cualidades tales como seriedad, generalidad, profundidad, inevitabilidad, economía de pensamiento, transparencia, sobriedad, adecuación... La seriedad se manifiesta en las ideas que pone en conexión, que normalmente dan lugar, en su desarrollo, a una buena porción del campo matemático en que tal hecho se encuentra, ya sea porque el método que lo crea es la clave que impregna dicho campo, ya sea porque el hecho en cuestión es el germen de todo ese cuerpo matemático. La generalidad se ha de dar con una cierta mesura. La generalización por sí misma no es en muchos casos más que el producto de una manía, sin gran valor; pero es cierto que un hecho demasiado concreto no despierta una gran admiración. Los matemáticos suelen calificar un método de "elegante" para indicar el tipo de sobriedad, economía de medios y transparencia que a veces se encuentra en la demostración de tal o cual teorema o hecho matemático. El proceso diagonal de Cantor, el método de dualidad en geometría proyectiva son ejemplos característicos de esta cualidad. Allí donde hay belleza matemática, ésta no se agota y su contemplación nunca deja de producir ese sentimiento de satisfacción, adecuación y acabamiento que una obra arquitectónica perfecta produce en el ánimo de quien la contempla.
La cualidad artística de la matemática se manifiesta asimismo en el proceso de su creación, que participa mucho de las características del proceso creativo de cualquier otro arte. Existe un magnífico estudio psicológico de J. Hadamard, gran matemático él mismo, sobre el proceso creativo en matemáticas (The psichology of invention in the mathematical field, Princeton University Press, 1945). Otro de los clásicos sobre este tema es un artículo famoso, muchas veces reproducido, de Poincaré (L'invention mathématique). Quien no haya tenido alguna experiencia creativa en matemáticas no podrá menos de sentirse asombrado ante las observaciones de Poincaré sobre el proceso matemático. A juzgar por el papel que desempeña la intuición, la inspiración, el trabajo y el descanso, y aun el sueño, o el ensueño, uno pensaría asistir a la composición de una sinfonía musical. Y en este sentimiento de dádiva repentina que la creación matemática comporta a menudo coinciden muchos matemáticos famosos como atestigua el mismo estudio de Hadamard. Por eso puede afirmar Poincaré con toda razón: "Puede extrañar el ver apelar a la sensibilidad a propósito de demostraciones matemáticas que, parece, no puede interesar más que a la inteligencia. Esto sería olvidar el sentimiento de belleza maternática, de la armonía de los números y las formas, de la elegancia geométrica. Todos los verdaderos matemáticos conocen este sentimiento estético real. Y ciertamente esto pertenece a la sensibilidad. Ahora bien, ¿cuáles son los entes matemáticos a los que atribuímos estas características de belleza y elegancia y que son susceptibles de desarrollar en nosotros un sentimiento de emoción estética? Son aquellos cuyos elemento están dispuestos armoniosamente, de forma que la mente pueda sin esfuerzo abrazar todo el conjunto penetrando en sus detalles. Esta armonía es a la vez una satisfacción para nuestras necesidades estéticas una ayuda para la mente, a la que sostiene y guía. Y al mismo tiempo, al colocar ante nuestros ojos un conjunto bien ordenado, nos hace presentir una ley matemática... Así, pues, es esta sensibilidad estética especial la que desempeña papel de criba delicada de la que hablé antes. Esto permite . comprender suficientemente por qué quien no la posee no será nunca un verdadero creador".
El que la matemática participe, efectivamente, de la condición de creación artística no da, por supuesto, carta blanca a los matemáticos para entregarse a un esteticismo estéril. La calidad artística de la matemática es como una dádiva con la que se encuentran quienes se dedican a esta actividad que es, al mismo tiempo y en grado muy intenso, ciencia y técnica. A este propósito resultan muy acertadas las sensatas observaciones de uno de los mayores matemáticos de nuestro tiempo, creador él mismo de un sinfín de campos matemáticos diversos. Así dice John von Neumann en su artículo The Mathematician: "A medida que una disciplina matemática se separa más y más de su fuente empírica o aún más si está inspirada en ideas que provienen de la realidad de un modo sólo indirecto, como de segunda o tercera mano, está más cercada por graves peligros. Se va haciendo más y más esteticismo puro, se convierte más y más en un puro arte por el arte. Esto no es necesariamente malo si el campo en cuestión está rodeado de otros campos relacionados con él que tengan todavía conexiones empíricas más cercanas, o si la disciplina en cuestión está bajo la influencia de personas dotadas de un gusto excepcionalmente bien desarrollado. Pero existe un grave peligro de que este campo venga a desarrollarse a lo largo de las líneas de menor resistencia, de que la corriente, tan lejos de su fuente, venga a disgregarse en una multitud de ramas insignificantes y de que la disciplina venga a convertirse en una masa desorganizada de detalles y complejidades. En otras palabras, a gran distancia de su fuente empírica, o bien después de mucha incubación abstracta, un campo matemático está en peligro de degeneración".
Matemática como instrumento de exploración
La matemática es también un instrumento de exploración de la naturaleza. Aristóteles ha expresado así el caracter "liberal" de la matemática en su mismo nacimiento: "Pero una vez que todas las técnicas necesarias se constituyeron, se vieron surgir ciencias cuyo objeto no puede ser ni la comodidad ni la necesidad. Nacieron primero en los climas donde el hombre puede entregarse más fácilmente al ocio y así las ciencias matemáticas nacieron en Egipto, donde la casta de los sacerdotes ocupaba de esta manera sus ocios" (Metafísica, Libro I, cap. 1, v.18).
La observación es interesante y expresa la concepción predominante en la Grecia clásica sobre el caracter desligado de toda consideración utilitaria de la matemática. Pero la afirmación de Aristóteles es falsa. La matemática occidental surgió primero entre los babilonios con fines prácticos bien concretos, económicos y astronómicos.
Las tablillas babilónicas que se conservan son un buen testimonio de ello. Hacia el siglo VIII a. de C. se puede decir que la astronomía babilónica alcanza un grado de desarrollo capaz de medir con bastante exactitud y predecir diversos fenómenos astronómicos. Se podría pensar que este tipo de aplicación práctica no es el mismo al que la técnica moderna nos tiene acostumbrados. La astronomía de aquel tiempo, podría suponerse, era especulativa. Pero no es cierto, pues los astrónomos babilonios seguían una finalidad práctica con sus mediciones y observaciones. Se trataba de elaborar con ellas los calendarios y vaticinios para sus monarcas. El carácter especulativo y contemplativo de las matemáticas predominó entre los griegos. La matemática pura tal como hoy la conocemos es creación de los matemáticos griegos de los siglos VI al III a. de C. culminando su creación con los Elementos de Euclides, que constituyen una recopilación del saber profesional hasta entonces.
El carácter práctico y aplicado de la matemática aparece esporádicamente en la obra de Arquímedes, por ejemplo, quien llega a presentar sus invenciones casi como una aberración por la que pide disculpas. Así lo explica Plutarco en la vida de Marcelo, el general romano que conquistó la ciudad de Siracusa después de un largo asedio: "... aunque sus inventos le habían dado la fama de poseer una sagacidad más que humana no se dignó dejar tras de sí ningún trabajo escrito sobre tales materias, sino que, considerando como innoble y sucio el objeto de la mecánica y toda suerte de artes dedicadas a la utilidad y al provecho, puso toda su ambición en aquellas especulaciones cuya belleza y sutileza no están teñidas por ningún color que aluda a las necesidades ordinarias de la vida".
Aplicabilidad de la matemática
La matemática aplicada se refugia sobre todo en la astronomía, que en el período helenístico alcanzó un enorme grado de desarrollo, culminando en la obra de Ptolomeo, el Almagesto, compendio de toda la evolución milenaria de la astronomía. La razón profunda de esta situación se debe buscar en el hecho de que los fenómenos astronómicos resultan estar más cerca de la abstración, con su relativa simplicidad y pureza, comparados con los fenómenos inmediatos al hombre. Las órbitas de los planetas, casi circulares, su repetición rítmica, hacen de los fenómenos astronómicos algo muy cercano al experimento analítico, que ni babilonios, ni egipcios, ni griegos conocieron. Esta circunstancia motivó que, desde la antigüedad y a través de la Edad Media, hubiese una ruptura fundamental entre el mundo de los astros y el mundo sublunar. El primero, de naturaleza cuasidivina, sujeto a las leyes exactas y cuantitativas de la matemática. El segundo, enturbiado por la presencia de fuerzas confusas no fácilmente inteligibles ni comprensibles por el entendimiento humano. La ciencia moderna se caracteriza por la superación de esta repugnancia a considerar el mundo de los astros y el mundo sublunar como sujetos a las mismas leyes y a tratar de cuantificar los fenómenos terrestres, caída de los cuerpos (Galileo), atracción gravitatoria (Newton), etcétera. La conjunción de este cambio de mentalidad con la invención de un método tan poderoso como el análisis matemático (hechos de ningún modo independientes) dieron lugar al nacimiento, en primer lugar, de la física moderna y, más tarde, a la tendencia generalizada hacia la matematización de todas las disciplinas del saber humano.
La aplicabilidad de las matemáticas se ha calificado como un misterio difícil de entender. Tal vez a un nivel elemental el hecho no parezca tan sorprendente. La aplicabilidad de la noción de número en la vida cotidiana del hombre, presente ya en las culturas más primitivas, parece un hecho que no necesita mucha explicación. Y sin embargo detrás de este hecho se esconde el mismo misterio que subyace a la extraña adecuación a realidades más complicadas de las teorías matemáticas más complejas. El matemático observa el mundo real dentro de sí mismo y en su entorno, abstrae unas cuantas propiedades que a él le interesa destacar, con ellas construye su mundo mental abstracto que pone en movimiento mediante las leyes básicas de su mente. Guiado por su intuición y sentido estético dirige su construcción escogiendo unas cuantas de las infinitas posibles estructuras que podría crear. Descubre así un complejo mundo mental, que él ha perseguido por su coherencia, armonía, belleza intrínseca. Y de repente, o paulatinamente, según los casos, observa que cierta parcela del mundo real es iluminada y plenamente explicada mediante aquella teoría matemática que hasta entonces se había mostrado alejada de la realidad. Esta vivencia está constantemente presente en la historia de la matemática. El misticismo filosófico de los pitagóricos del siglo VI a. C. es probablemente una respuesta a ella, como lo es ciertamente el de Kepler en el siglo XVII. Apenas se puede uno imaginar la sensación de congruencia y belleza que éste debió de experimentar al comprobar que la teoría de las cónicas, tan cultivada y perfeccionada por sí misma desde los días de Apolonio de Pérgamo (s. III a. C.), se adaptaba plenamente a la explicación del movimiento planetario, viendo que elementos con significado en apariencia puramente matemático como los focos de tales cónicas adquirían una significación física tan importante (el Sol ocupa uno de los focos de cada una de las cónicas descritas por los planetas). El entusiasmo de Kepler ante esta coherencia, como en el caso de los pitagóricos, explica y justifica sus extrapolaciones místicas en su obra Harmonice mundi.
Aplicabilidad de la matemática
La razón más profunda de esta especie de armonía pre-establecida que se puede observar en la aplicabilidad de la matemática al mundo real está íntimamente ligada al problema filosófico fundamental de la teoría del conocimiento, en el que no qusiera introducirme aquí. Me limitaré a iluminar este punto con tres testimonios recientes. J. von Neumann escribe: "Yo creo que constituye una aproximación relativamente buena a la verdad -una verdad tan complicada que otra cosa que una aproximación a ella es impensable- el decir que las ideas matemáticas se originan en la experiencia, si bien su genealogía es a veces larga y oscura. Sin embargo una vez se han estructurado a partir de ella comienzan una vida peculiar, independiente, y se podría comparar el objeto matemático de la forma más adecuada con un sujeto creador, al que subyacen casi exclusivamente motivaciones estéticas, pero en ningún modo se puede comparar con una ciencia empírica". En su artículo sobre L'architecture des mathématiques, N. Bourbaki afirma: "Que existe una relación íntima entre los fenómenos experimentales y las estructuras matemáticas parece confirmarse plenamente de la forma más inesperada mediante los descubrimientos más recientes de la física contemporánea. Pero no sabemos absolutamente nada sobre los fundamentos de este hecho (suponiendo que se pudiera encontrar realmente significación a estas palabras) y tal vez no lleguemos a saber nunca sobre ello". Por su parte, E. P. Wigner cierra su famoso artículo The unreasonable effectiveness of mathematics in the natural sciences con estas palabras: "el milagro de la adecuación del lenguaje de la matemática para la formulación de las leyes físicas es un don maravilloso que ni entendemos ni merecemos. Deberíamos mostrarnos agradecidos por él y esperar que permanecerá siendo válido en la investigación futura y que se extenderá, para bien o para mal, para placer nuestro aunque también tal vez para nuestra perplejidad, a ramas más amplias del saber".
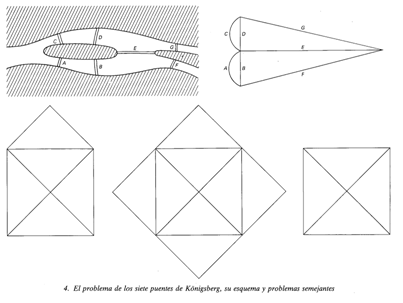
La matemática es también un juego. "Un buen juego matemático vale por muchos teoremas" ha afirmado uno de los grandes matemáticos de nuestro tiempo, J. E. Littlewood. El carácter lúdico de las matemáticas ha estado presente en ellas desde antiguo. Como ya hemos tenido ocasión de ver, Aristóteles considera las matemáticas hasta cierto punto como la ocupación de los ociosos sacerdotes egipcios. El tipo de reto intelectual que la geometría elemental o la teoría de números presenta difiere muy poco del que se encuentra en multitud de acertijos populares. Una buena proporción de la matemática seria de nuestros textos debe su nacimiento a un profundo acertijo o juego matemático. Así comenzó, por ejemplo, la topología: "el problema que, según entiendo es muy bien conocido, se enuncia así: en la ciudad de Kónigsberg, en Prusia, hay una isla, llamada Kneiphof, rodeada por los dos brazos del río Pregel. Hay siete puentes A, B, C, D, E, F y G, que cruzan los dos brazos del río (ver el recuadro 4). La cuestión consiste en determinar si una persona puede realizar un paseo de tal modo que cruce cada uno de los puentes una sola vez. Se me ha informado de que mientras unos negaban la posibilidad de hacerlo y otros lo dudaban, nadie sostenía que fuese posible realmente"'. Con estas palabras introduce Euler el problema de los siete puentes de Königsberg, iniciando así un nuevo género de consideraciones matemáticas que darían lugar a la moderna topología. El problema que se propone aquí es equivalente, como se observa fácilmente reduciendo la isla y las zonas de tierra a sendos puntos y los puentes a arcos que los unen, al de dibujar la figura indicada sin levantar el lápiz del papel y sin recorrer cada línea más de una vez. Un problema semejante al de dibujar, con las mismas condiciones, las figuras indicadas a continuación que todos hemos conocido de niños.
Ha habido muchos problemas famosos con aspecto de enigmas de la esfinge que han dado lugar a la creación de teorías matemáticas. Tal tipo de problemas abunda extraordinariamente en el campo de la teoría de números. Muchos están aún por resolver. He aquí algunos: ¿Es cierto que para ningún entero n mayor que 2 y ningún trío de números enteros positivos x, y, z mayores que 0 se verifica x' + y' = z? (problema de Fermat); ¿es cierto que todo número par es suma de dos números primos? (conjetura de Goldbach); ¿existen infinitos pares de números primos (p,q) tales que q = p + 2? (problema de los números primos hermanos).
El famoso problema de los cuatro colores (¿es posible colorear adecuadamente un mapa cualquiera con cuatro colores o existirá un mapa que necesite cinco colores para que los países vecinos se distingan apropiadamente?) nació como curiosidad de un estudiante de Cambridge en 1852. El problema ha estimulado por más de un siglo el trabajo de innumerables matemáticos y ha sido resuelto por Appel y Haken, de la Universidad de Illínois, en 1976 . Las implicaciones del método de resolución de esta cuestión, que nació como un rompecabezas curioso, sobre la estructura de la matemática futura están aún por ver. Lo que ahora es el teorema de los cuatro colores (cuatro colores bastan) ha sido demostrado mediante la intervención, hasta ahora totalmente imprescindible, del computador. Es decir, no se conoce ninguna cadena de razonamientos del tipo de la matemática de siempre, asequible por la mente humana sin la ayuda de aparatos externos, que conduzca al teorema. Este hecho nuevo en la historia de la matemática plantea cuestiones profundas y muy interesantes sobre el porvenir de la matemática. ¿Será tal vez imposible construir una demostración manejable sin computador? ¿Qué grado de certeza proporciona una demostración de este tipo? Nuestra evidencia es sustituída por la fiabilidad del computador. ¿Cuántos y qué tipo de problemas abiertos en matemáticas esperan una solución semejante? ¿Acaso el problema de Fermat o la conjetura de Goldbach puedan resolverse de modo análogo? ¿Modificará sustancialmente el computador nuestra forma de proceder como matemáticos?
El juego matemático sigue atrayendo intensamente tanto a matemáticos como a no matemáticos. Prueba de ello es, por ejemplo, la constancia del éxito de la sección permanente de Martin Gardner por tantos años en esta revista. De vez en cuando aparecen en el mundo juegos matemáticos, en nuestros días el cubo de Rubik, que por su capacidad de atracción se convierten en el entretenimiento intenso de millones de personas por muchas horas. Es una verdadera lástima que el contenido lúdico y artístico de la matemática no sea explotado más a fondo por los enseñantes a todos los niveles, pero sobre todo en los primeros pasos de la educación matemática. A mi parecer la incapacidad confesada para las matemáticas de muchas personas altamente cultivadas, competentes en otras actividades y profundamente inteligentes, se debe sobre todo a un bloqueo psicológico inicial, originado por los métodos equivocados de enseñanza.
La matemática aventura del pensamiento
Vayamos, por fin, a la matemática como aventura del pensamiento. Heidegger ha hablado de "eterno aburrimiento del avance rectilíneo de la matemática", observación compartida por muchos que se maravillan de que en esta ciencia haya todavía algo por hacer. Tal ignorancia puede ser disculpada por el hecho de que así como para hablar de otras muchas actividades del espíritu humano sólo se precisa un poco de audacia y otro poco de información, de las matemáticas sólo se puede hablar desde dentro; sólo quien ha asimilado el método matemático y ha tratado de manejarlo está capacitado para entender lo que la creación matemática comporta.
La matemática es una actividad profundamente humana y como tal ha participado y participa intensamente de las vicisitudes históricas del hombre. Está sujeta, al igual que todas las artes, a las modas, corrientes y catástrofes que afectan al hombre. Por ejemplo, la decadencia del pueblo griego y la supremacía del romano, menos dotado para la especulación que el primero, fue causa de un estancamiento de la matemática de Occidente por muchos siglos. La adopción de un simbolismo inapropiado retrasó en unos cincuenta años el desarrollo de las matemáticas en Inglaterra. A una escala temporal más reducida, es evidente que existen modas y corrientes que producen fluctuaciones más o menos intensas en la actividad matemática a todos los niveles, influyendo tanto en la formación de quienes comienzan como en la actividad de los matemáticos de vanguardia,
La matemática participa efectivamente de modo intenso de los avatares históricos del hombre. Pero es que, además, en su mismo progreso intrínseco, la matemática tiene todos los trazos de una apasionante aventura del espírítu. En ella abundan los momentos de incertidumbre y confusión, tales como el apercibimiento por los pitagóricos de la existencia del número irracional, como su nombre indica (alogos arizmos), un monstruo que no encaja en el armazón cristalino y límpido de la matemática pitagórica.
En lugar de enfrentarse con el reto que representaba este contratiempo, o de saber convivir con él, la matemática griega abandonó un tanto el desarrollo del número y se dedicó más intensamente al cultivo de la geometría, lo que tuvo consecuencias importantes en la evolución de la matemática. La aparición del número imaginario fue encajada con más pragmatismo por los algebristas del Renacimiento, que aprendieron a manejarlo aceptablemente incluso sin entender su naturaleza. Ha habido otros muchos períodos importantes de perplejidad y polémica intensa. Las paradojas de Zenón en el siglo V (Aquiles y la tortuga, la dicotomía, la flecha,...), que tratan de poner de manifiesto la incapacidad humana para dominar los procesos infinitos, debieron de causar una sensación de callejón sin salida semejante a la que los matemáticos del siglo XX han experimentado cuando empezaron a aparecer las paradojas de la teoría de conjuntos que cuarteaban lo que había comenzado a ser considerado como base de todo el edificio de las matemáticas. Ante esta situación y ante los teoremas descubiertos por Gödel y los lógicos modernos, que ponen bien en claro, entre otras cosas, la incapacidad de la matemática para colocar sus propias bases fuera de toda duda (imposibilidad de demostrar la consistencia, es decir, la ausencia de contradicción, del edificio matemático), constituyen una expresión típica del sentir de los matemáticos contemporáneos las siguientes palabras de N. Bourbaki en L'architecture des mathématiques: "Creemos que la matemática está destinada a sobrevivir y que jamás tendrá lugar el derrumbamiento de este edificio majestuoso por el hecho de una contradicción puesta de manifiesto repentinamente, pero no pretendemos que esta opinión se base sobre otra cosa que la experiencia. Es poco, dirán algunos. Pero desde hace 25 siglos los matemáticos tienen el hábito de corregir sus errores y de ver así su ciencia enriquecida, no empobrecida. Esto les da el derecho de arrostrar el porvenir con serenidad".
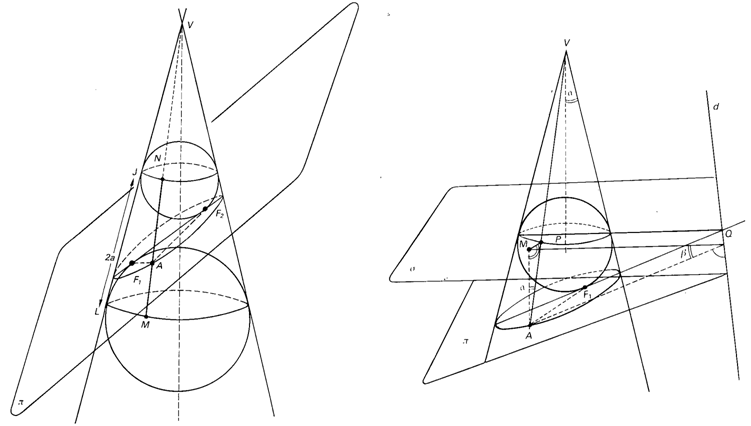
Figura 1
1. La elipse es la sección obtenida al cortar el cono circular recto por un plano pi que forma un ángulo con el eje del cono mayor que el ángulo que forman las generatrices del cono con dicho eje. Trazando las dos esferas indicadas en la figura de la izquierda tangentes a pi en F1, y F2 y a todas las generatrices del cono y trazando una generatriz r cualquiera, se observa que AF1 = AM, AF2 = AN, AF1 + AF2 = MN = constante. Así, para cada punto de la elipse la suma de sus distancias a los dos focos AF1 + AF2, es constante e igual al eje mayor de la elipse (figura de la izquierda). Asimismo, la figura de la derecha nos muestra, trazando el plano sigma que contiene el círculo de la esfera superior, la recta d intersección de pi y sigma, la proyección M de A sobre sigma y la proyección Q de M sobre d, que AQ/AF1= AQ/AP = (AM/cos beta) / (AM/AM/cos alfa) = cos alfa/cos beta = constante. Por tanto, para cada punto de la elipse la razón de distancias a una recta fija d y al foco F es constante (excentricidad).
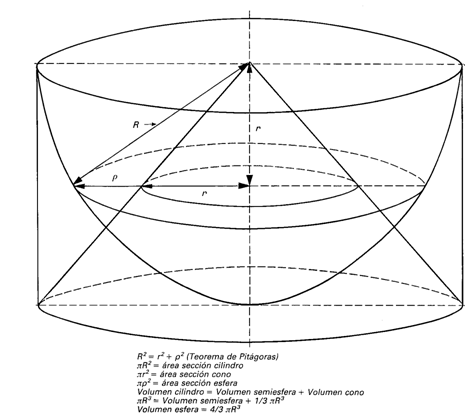
2. Modo en que probablemente Arquímedes de Siracusa (287-212 a. C.)
descubrió el hecho de que el volumen de la esfera de radio R es (4/3)piR^3. Si
se considera, como se indica en la figura, el cilindro recto circunscrito a la
esfera y el cono con vértice en el centro de la esfera y base la del cilindro,
y a continuación se observan las secciones de los tres cuerpos por un plano
paralelo a la base común del cilindro y del cono, es facildeducir, mediante el
teorema de Pitágoras, que el área de la sección en el cilindro es la suma de
las áreas de las secciones producidas en el cono y en la esfera. Como esto es
válido para cada plano paralelo a la base se puede deducir, mediante el
métodode exhausción de Eudoxo (s. IV a. C.), que el volumen de la semiesfera es
igual al del cilindro pi R^3menos el del cono 1/3 piR^3. Es decir, el volumen
de la esfera es 4/3 pi R^3.
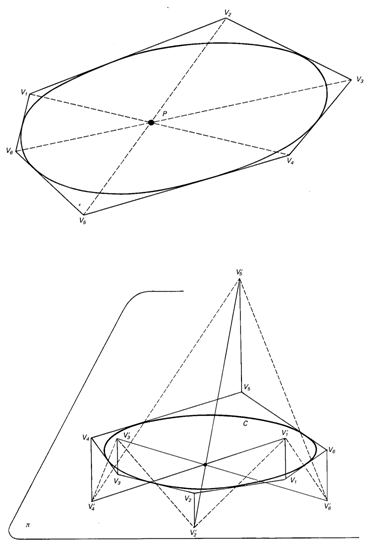
3. El hexagrama místico. El teorema de Brianchon (primera figura de las de arriba) afirma que si en un círculo (o en una cónica cualquiera) se circunscribe un hexágono arbitrario, las tres diagonales que unen vértices opuestos se cortan en un punto. La siguiente demostración, publicada por el autor por primera vez en 1976, es un buen ejemplo de las características del tipo de belleza que tantas veces se presenta en los hechos y métodos matemáticos. Se basa en las dos sencillas observaciones siguientes:
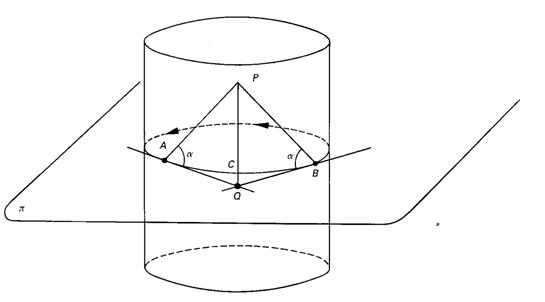
(1) Si se fija un sentido sobre un círculo C en el plano pi (tercera figura de las de arriba), se toman dos puntos A y B sobre C, se trazan semirrectas tangentes a C en A y B respectivamente en sentido contrario y finalmente se toman dos rectas hacia arriba tangentes al cilindro recto de sección C formando ángulos de igual magnitud con el plano pi, entonces estas dos rectas se cortan en un punto P (o bien son paralelas si A y B son diametralmente opuestos). La proyección de P sobre pi es el Punto Q intersección de las dos semirrectas tangentes en A y B. Y recíprocamente, si se toman Q, se toma P situado en la vertical sobre Q y se une P con A y B, entonces los ángulos PAQ y PBQ son iguales.
(2) Tres rectas en el espacio que se cortan dos a dos y no están en un mismo plano pasan las tres por un mismo punto del espacio. Con estas dos observaciones el teorema resulta de modo sencillo.
Se considera el círculo C en el plano pi y el hexágono circunscrito V1V2V3V4V5V6 (segunda figura de las de arriba).Por V, levantamos una perpendicular a pi hasta un punto arbitrario V'. Unimos V1 al punto de tangencia de V1 V2 a C y prolongamos hasta cortar la perpendicular por V2 a pi en V'2. Procediendo así sucesivamente obtenemos en el espacio V'1 V'2 V'3 V'4 V'5 V'6y volvemos a V1. Consideremos ahora V'1 V'4 y V'2 V'5. Observemos que V'1V'2 y V'4 V'5 son dos rectas en la situación de la observación (1). Así, o son paralelas o se cortan. Por tanto V'1 V'4 y V'2 V'5están en un plano y, así, o bien son paralelas o se cortan. Se excluye que sean paralelas por construcción. Así se cortan. Lo mismo vale para V'2V'5 y V'3V'6. Se cortan. También V'1V'4 Y V'3V'6 se cortan. Usando la observación (2) resulta que las tres rectas se cortan en un punto, pues no están en un mismo plano por construcción. Por tanto sus proyecciones sobre pitambién, pero éstas son precisamente las diagonales V1V4, V2V5, V3V6.