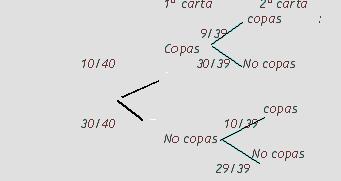
5ª Parte: Estadística y Probabilidad (del cuaderno actividades de 3º ESO)

 

1. Las notas de los 20 alumnos de una clase son:

                   4, 3, 3, 5, 6, 7, 9, 0, 5, 4, 9, 10, 2, 7, 2, 2, 5, 6, 5, 0

Haz una tabla de frecuencias.

Solución

Variable	Frecuencias	absolutas	Frecuencias     relativas
estadística  xi	puntuales ni	acumuladas Ni	puntuales fi	acumuladas Fi
0 2 3 4 5 7 9	2 3 2 2 5 3 3	2 5 7 9 14 17 20	1/10 3/20 1/10 1/10 1/4 3/20 3/20	1/10 5/20=1/4 7/20 9/20 14/20=7/10 17/20 20/20=1

 

 

2. Del alumbramiento de un conjunto de ratas se ha observado el número de crías, obteniéndose los siguientes valores numéricos:

5, 3, 1, 5, 3, 6, 4, 2, 5, 6, 3, 6, 5, 2, 6, 7 y 3.

Haz una tabla de frecuencias.

 

3. En un Instituto hay matriculados 2200 alumnos que se distribuyen por edades en la forma siguiente: 215 de 14 años, 437 de 15, 421 de 16, 396 de 17, 512 de 18, 124 de 19 y 95 de 20. Formar la tabla de distribución y de frecuencias, que incluya frecuencias acumuladas.

 

4. . En una Caja de Reclutamiento se toma una muestra de tamaño 30 de los pesos de los mozos correspondientes a un cierto reemplazo, obteniéndose los siguientes datos medidos en kg:

71.9, 63.9, 62.3,  72.5, 78.0, 70.7, 71.4, 60.5, 60.9, 68.2, 88.5, 76.1, 82.1, 63.7, 79.8, 67.5, 50.1, 69.5, 66.1, 47.3, 72.1, 59.8, 93.7, 80.7, 61.2, 64.3, 53.7, 74.7, 96.3, 73.2.

Construir una tabla de frecuencias agrupando los datos en clases de la misma amplitud.

Solución

 A continuación se presenta la misma muestra ordenada:

47.3, 50.1, 53.7, 59.8, 60.5, 60.9, 61.2, 62.3, 63.7, 63.9, 64.3, 66.1, 67.5, 68.2, 69.5, 70.7, 71.4, 71.9, 72.1, 72.5, 73.2, 74.7, 76.1, 78.0, 79.8, 80.7, 82.1, 88.5, 93.7, 96.3.

Tomaremos 6 intervalos de amplitud 10, la tabla queda estructurada de la siguiente manera:

clases	Marcas de clase	frecuencias absolutas de clase     ½acumuladas		Frecuencias relativas de clase   ½acumuladas
45 -55 55 -65 65 -75 75 -85 85 -95 95 -105	50 60 70 80 90 100	3 8 11 5 2 1	3 11 22 27 29 30	0.1 0.266 0.366 0.166 0.066 0.033	0.1 0.366 0.733 0.900 0.966 1

                                          30                               0.997»1

 

5. El número de personas que viven en cada uno de los portales de una gran barriada es:: 63, 58, 70, 47, 120, 76, 80, 59, 80, 70, 63, 77, 104, 97, 78, 90, 112, 88, 67, 58, 87, 94, 100, 74, 55, 80, 75, 49, 98, 67, 84, 73, 95, 121, 58, 71, 66, 87, 76, 56, 77, 82, 93, 102, 56, 46, 78, 67, 65, 95, 69, 90, 58, 76, 54, 76, 98, 49, 87, 69, 80, 64, 65, 56, 69, 68, 99, 106.

Construye una tabla de frecuencias^[1].

 

6. La producción editorial española de libros de sociología y Estadística, en los años que se indica es:

Años	1991	1992	1993	1994	1995	1996	1997
nº	345	487	589	376	479	652	741

Hacer una tabla de frecuencias absolutas y relativas puntuales. Expresar la relativa en porcentajes.

 

7.  El censo, en miles de cabezas, del ganado en el territorio español, en  1994 fue:

Ganado	Número de cabezas
Bovino Ovino Caprino Porcino Caballar Mular Asnar	5300 18047 2601 12308 264 153 164

Dibujar un diagrama de sectores y otro de rectángulos.

 

8. Los jugadores de un determinado equipo de baloncesto se clasifican, por altura, según la tabla siguiente:

Altura	1,70-175	1,75-1,80	1,80-185	185-190	1,90-1,95	1,95-2,00
Nº de jugadores	1	3	4	8	5	2

Dibujar el polígono de frecuencias absolutas acumulativo.

 

9. Hallar la media y la varianza de la variable cuyos valores y frecuencias absolutas vienen dadas en la tabla adjunta

b) Representar gráficamente los datos en un diagrama de barras.

Solución a) la media es:

0 2 3 4 5 7 8	3 1 1 4 3 2 1	0 2 3 16 15 14 8	0 4 9 16 25 49 64	0 4 9 64 75 98 64
	15	58		314

Se tiene :

La varianza:   =, foma que se usa en la tabla II

= 5,96

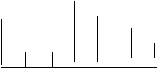b)

 

 

   0    2     3     4    5        7    8

10.a) Completar los datos que faltan en la siguiente tabla estadística, donde f, F y f_r representan, respectivamente, la frecuencia absoluta, acumulada y relativa:

b) Calcula la media, mediana y moda de esta distribución

11. Se ha pasado un test de 79 preguntas a 600 personas. El número de respuestas correctas se refleja en la siguiente tabla:

intervalos	mi	f. abs. puntual	f. abs. acumulada	f. rel. puntual	f. rel. acumulado
[0, 10) [10, 20) [20. 30) [30, 40) [40, 50) [50, 60) [60, 70) [70, 80)	5 15 25 35 45 55 65 75	40 60 75 90 105 85 80 65	40 100 175 265 370 455 535 600	1/15 1/10 1/8 3/20 7/40 17/120 2/15 13/120	1/15 1/6 7/24 53/120 37/60 91/120 107/120 1
		600		1

a) Dibuja un histograma y un polígono de frecuencias acumuladas.

b) Calcula la media, el intervalo mediano, la desviación típica.(utiliza la tabla II)

Problemas de probabilidad

 

1.a)  Encuentra el espacio muestral del experimento lanzar dos monedas. b) Si se define el suceso A =“al menos una sea cara”, ¿de cuántos sucesos elementales consta A?

 

2. . Si consideramos el suceso A = sacar dos cruces, al lanzar dos monedas, calcula el complementario de A.

 

3. Se extraen dos cartas de una baraja española. Si A = “ las dos sean copas” y  B = “ una sea copas y la otra rey” , calcula A Ç B

 

4. Comenta cada una de las siguientes afirmaciones:

a). No es muy probable que me toque la lotería.

b) Una profesora de inglés aprobó el curso pasado al 80% de sus alumnos. Este año me ha tocado con ella así que lo más probable es que apruebe.

c). Una pareja ha tenido 4 hijos, todos ellos niños. Luego lo más probable es que el próximo sea niña.

d) Me han dicho que sufre un accidente un avión de cada 1000. Me he informado bien, y resulta que el último vuelo que ha salido es el número 999 sin haber sufrido accidente ninguno de ellos, así que no se te ocurra coger el próximo avión.

5. Lanzar un dado 30 veces y calcula las frecuencia relativa del suceso obtener un 6.

 

4. Consideremos el experimento lanzar dos monedas al aire. Calcular la probabilidad del  suceso sacar una cara y una cruz.

5. Calcula la probabilidad de obtener dos 6 al lanzar dos dados.

 

6. Se extrae una bola de una bolsa que contiene 4 bolas blancas, 5 rojas y 2 negras. ¿Cuál es la probabilidad de que no sea negra?

 

8 ¿Cuál es la probabilidad de que al tirar dos dados la suma de puntos obtenidos sea 5?.

 

9. Calcular la probabilidad de obtener un as ó una copa al extraer una carta de una baraja española.

 

11. En una determinada localidad hay tres partidos políticos: PP, PSOE e IU. Se efectúa un referéndum para decidir si un cierto día se declara fiesta local. La siguiente tabla nos da los resultados en % en función del partido al que votó cada ciudadano en las últimas elecciones:

	PP	PSOE	IU	Abs.
Sí	25	20	8	12
No	15	10	2	8

a) ¿Qué probabilidad hay de que una persona tomada al azar haya votado Sí en el referéndum?

b) Calcular la probabilidad de que un individuo sea del PP sabiendo que ha votado sí.