APLICACIONES LINEALES
(RESUMEN TEÓRICO Y EJERCICIOS RESUELTOS)
Definición. Sean V y W dos espacios vectoriales sobre un mismo cuerpo K. Una aplicación f: V-----à W se dice que es lineal si verifica:
1)
f(x
+ y)= f(x)+f(y)
2)
y 
f(tx)=tf(x)
Ejemplo 1. Consideremos en R2 la proyección ortogonal sobre el eje de abscisas, es decir definamos P: R2 -----à R, P(x1, x2)=x1
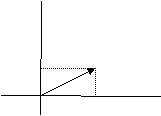
Se puede comprobar fácilmente que P es una aplicación lineal.
x2
x1
Ejemplo 2. Se define la aplicación f: R3 -----à R2
f(x1, x2, x3)= (x1+ x2, x2-x3)
f es lineal.
En efecto sean x =(x1, x2, x3), y = (y1, y2, y3) , se tendrá x +y = (x1+ y1 , x2 + y2, x3+ y3)
f (x + y)= f(x1+ y1 , x2 + y2, x3+ y3)=( x1+ y1 + x2 + y2, x2 + y2-( x3+ y3))=( x1+ x2, x2 - x3)+ ( y1+ y2, y2 - y3)=f(x)+f(y)
Análogamente f(tx) = tf(x) (comprobarlo)
Caracterización de aplicaciones lineales
f es lineal 
f(t x + s y)= t f(x)+ s f(y) para
todo x, y perteneciente a V y para todo t y s pertenecientes a K. (trivial)
Teorema 1. Sea f una aplicación lineal entre dos espacios vectoriales V y W. Se tiene:
1) f(0V)= 0W.
2) f(-x)=-f(x).
3) Si x1, x2,..., xp son
vectores de V y t1, t2,....,tp pertenecen a K 
f(t1x1
+t2x2+....+tpxp)=t1f(x1)+t2f(x2)+…..+tpf(xp).
4) Si el conjunto 
es linealmente dependiente (l.d.
)entonces 
es
l.d.
Corolario. Si es un
conjunto de vectores de V y es linealmente independiente (l.i
) entonces es
l.i. El recíproco no es cierto.
Ejemplo 3. Sea f: R3 -----à R2 tal que f(x1, x2, x3)= (x1+ x2, -x3)
Sea v1=(1, 0, 0), v2=(1, 1, -1) y v2=(1, 0, 1). Se pide:
a) Probar que f es lineal
b)
Probar que 
es l. d.
Solución
a) Sea x=(x1, x2, x3), y=(y1, y2, y3) , t de k, se verifica:
f (x + y)= f(x1+ y1 , x2 + y2, x3+ y3)=( x1+ y1 + x2 + y2, -( x3+ y3)) =( x1+ x2, - x3)+ ( y1+ y2, - y3)= f(x)+f(y)
(comprobar que f(tx) = tf(x))
b) Se tiene f(v1)=f(1, 0, 0)=(1, 0), f(v2)=(2, 1) y f(v3)=(1,-1) que es ligado (evidente pues en R2 tres vectores son siempre ligados)
Observar
que 
era l.i.
Teorema 2. Sean f y g dos aplicaciones lineales definidas entre los espacios
vectoriales V y W. Sea 
una base de V. Si f(ui)=g(ui) i=1, ...., n entonces f= g
Observación 1. Este teorema nos indica que la aplicación lineal está determinada por las imágenes de una base.
Teorema 3. Sean una base de V y 
un conjunto
arbitrario de W. Entonces existe una única aplicación lineal
f: V-----à W tal que f(ui)=vi, i=1,...,n
Observación 2. Este teorema nos dice que para definir una aplicación lineal basta definir las imágenes de los vectores de una base del espacio vectorial V.
....
Problema 1. Para las aplicaciones que se citan, se comprobará si son o no lineales. En caso de que sean lineales, se describirá su imagen y su núcleo, calculando una base de cada uno de estos subespacios:
a) La aplicación f: R3---àR2 dada por: f(x, y, z)=(x2-y, x-y+z)
b) La aplicación f: R2---àR2 dada por: f(x, y)=(x, x-y)
c) La aplicación f: R3---àR2 dada por: f(x, y, z)=(x, 1, z)
d) La aplicación f: R3---àR3 dada por: f(x, y, z)=(z, x+y, -z)
e) La aplicación f: R4---àR3 dada por: f(x, y, z, t)= (x+y, t, z)
Solución
a) No es lineal
En efecto, si consideramos los vectores x=(2, 0, 0) e y=(1, 1, 0), por ejemplo, se tiene:
f(2, 0, 0)=(4, 2)
f(1, 1, 0)=(0, 0) y entonces : f(2, 0, 0)+f(1, 1, 0)=(4, 2)
Sin embargo, f((2, 0, 0)+(1, 1, 0))=f(3, 1, 1)=(8, 2)
b) Es lineal, en efecto:
f(t(x, y)+s(x’, y’)) = f(tx+sx’, ty+sy’)=(tx+sx’, tx+sx’ –( ty+sy’))= (tx, t(x-y))+(sx’, s(x’-y’))=t(x, x-y)+s(x’, x’-y’)=tf(x,y)+ sf(x’, y’)
Núcleo (Ker f)
f(x, y)=0 implica (x, x-y)=(0, 0), de donde x=y=0 y por lo tanto
el Kerf =
Imagen de f
Como dim R2=dim Imf + Ker f, se verifica que la dimensión de la imagen es 2 y por tanto Im f= R2.
c) No es lineal (trivial)
d) Es lineal (comprobarlo)
Núcleo de f (Ker f)
f(x, y, z)=(z, x+y, -z)=(0, 0, 0) implica z=0, x+y=0 de donde y=-x
una
base 
y
el Ker f= <(1, -1, 0)>
La dimensión de la imagen es 2,
(para hallar el subespacio imagen hay varios métodos, pero lo más cómodo es usar que el sistema formado por los transformados de una base es un sistema generador)
f(1, 0, 0)= (0, 1, 0)
f(0, 1, 0)=(0, -1, 0)
f(0, 0, 1)=(1, 0, -1)
Entonces Im f= <(0, 1, 0), (1, 0, -1)>
e) Es lineal
Comprobar que Ker f= <(1, -1, 0, 0)> y Imf =R3
En construccion